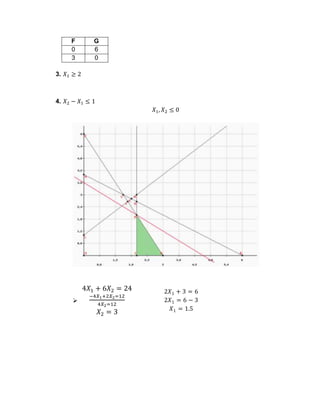
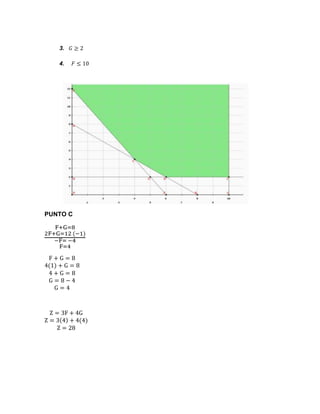
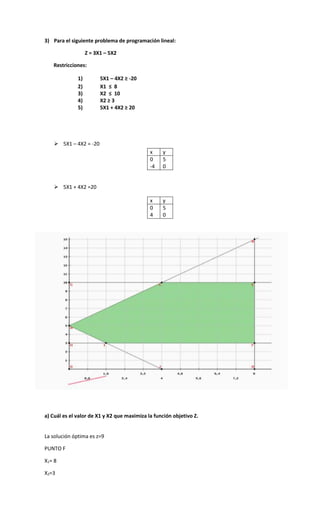
El documento presenta tres problemas de programación lineal. El primero involucra maximizar las utilidades de una fábrica de pintura sujeto a restricciones en las materias primas. La solución óptima es producir 1.5 toneladas de pintura interior y 3 toneladas de pintura exterior. El segundo problema busca minimizar los costos sujeto a restricciones de producción, arrojando una solución óptima de 4 unidades de F y 4 unidades de G. El tercer problema presenta un modelo de programación lineal para maximizar y minimizar una función objetivo sujet

1. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLITICAS Y ADMINISTRATIVAS
CONTABILIDAD Y AUDITORÍA
Docente: Doctor Marlon Villa
Discente: Lorena Alexandra Llerena Lucio
Fecha: 2014-10-22
Semestre: 5º “A”
Tema: Método Gráfico
C U E S T I O N A R I O.
Hallar el valor óptimo, la solución óptima, las restricciones activas, las restricciones inactivas, la
holgura o el excedente de los siguientes problemas.
1) Una fábrica de pintura produce pinturas para interiores y exteriores, a partir de dos materias
primas M1 y M2. Por cada tonelada de pintura para interiores se requiere 4 toneladas de M1 y
2 toneladas de M2. Y para cada tonelada de pintura para exteriores se requiere 6 toneladas de
M1 y una de M2. Se dispone de 24 toneladas de M1 y 6 de M2 diariamente. La utilidad que
arroga una tonelada de pintura para exteriores es de $ 5 000 y de una tonelada para interiores
es de $ 4 000. La demanda máxima diaria de pintura para interiores es de 2 toneladas. Además
la demanda diaria de pintura para interiores no puede exceder a la de pintura para exteriores
por más de una tonelada. La compañía quiere determinar la mezcla de producción óptima de
pinturas para interiores y exteriores que maximice las utilidades diarias y satisfaga las
limitaciones.
Maximizar: Z= 4000X1+ 5000X2
1. 4푋1 + 6푋2 ≤ 24
4푋1 + 6푋2 = 24
F G
0 4
6 0
2. 2푋1 + 푋2 ≤ 6
2푋1 + 푋2 = 6

2. 3. 푋1 ≥ 2
4. 푋2 − 푋1 ≤ 1
푋1, 푋2 ≤ 0

4푋1 + 6푋2 = 24
−4푋1+2푋2=12
4푋2=12
푋2 = 3
2푋1 + 3 = 6
2푋1 = 6 − 3
푋1 = 1.5
F G
0 6
3 0

3. HOLGURAS O EXCEDENTES

푿ퟐ − 푯 ≥ ퟐ
ퟏ. ퟓ − 푯 ≥ ퟐ
푯 = ퟐ

푿ퟏ − 푿ퟐ + 푯 ≤ ퟏ
ퟑ − ퟏ. ퟓ + 푯 ≤ ퟏ
푯 = ퟎ. ퟓ
2) MINIMIZAR: Z= 3F+ 4G
1. F + G ≥ 8
2. 2F + G ≥ 12
3. G ≥ 2
4. F ≤ 10
F , G ≥ 0
1. 퐹 + 퐺 ≥ 8
2. 2퐹 + 퐺 ≥ 12
VALORES
ÓPTIMOS
Z 21000
X1 1.5
X2 3
F G
0 8
8 0
F G
0 12
6 0
HOLGURA
EXCEDENTE

4. 3. 퐺 ≥ 2
4. 퐹 ≤ 10
PUNTO C
F+G=8
2F+G=12 (−1)
−F= −4
F=4
F + G = 8
4(1) + G = 8
4 + G = 8
G = 8 − 4
G = 4
Z = 3F + 4G
Z = 3(4) + 4(4)
Z = 28

5. SOLUCION ÓPTIMA
Z 28
F 4
G 4
HOLGURAS O EXCEDENTES

퐹 + 퐺 + 퐻1 = 8
4 + 4 + 퐻1 = 8
퐻1 = 8 − 8
퐻1 = 0

2퐹 + 퐺 + 퐻2 = 12
2(4) + 4 + 퐻2 = 12
퐻2 = 12 − 12
퐻2 = 0

퐺 − 퐻3 = 2
4 − 퐻3 = 2
−퐻3 = 2 − 4
−퐻3 = −2
퐻3 = 2
EXCEDENTE

퐹 + 퐻4 = 10
4 + 퐻4 = 10
퐻4 = 10 − 4
퐻4 = 6
HOLGURA

6. 3) Para el siguiente problema de programación lineal:
Z = 3X1 – 5X2
Restricciones:
1) 5X1 – 4X2 ≥ -20
2) X1 ≤ 8
3) X2 ≤ 10
4) X2 ≥ 3
5) 5X1 + 4X2 ≥ 20
 5X1 – 4X2 = -20
x y
0
-4
5
0
 5X1 + 4X2 =20
x y
0
4
5
0
a) Cuál es el valor de X1 y X2 que maximiza la función objetivo Z.
La solución óptima es z=9
PUNTO F
X1= 8
X2=3

7. b) Cuál es el valor de X1 y X2 que minimiza la función objetivo Z
La solución óptima es z= -38
PUNTO G
X1= 4
X2=10