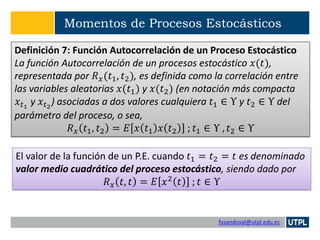
El documento aborda el análisis de procesos estocásticos, incluyendo su definición, clasificación, especificación y conceptos relacionados como momentos y funciones de densidad. Se presentan ejemplos prácticos y teorías sobre la estacionalidad y comportamientos de procesos estocásticos específicos, así como la autocorrelación y autocovarianza. Finalmente, se discuten casos de estudio como las transmisiones binarias semi-aleatorias y el ruido térmico en circuitos.




































![fasandoval@utpl.edu.ec
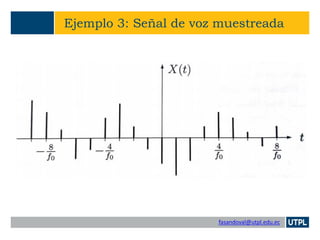
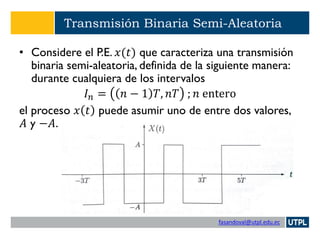
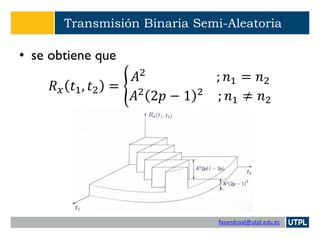
Transmisión Binaria Semi-Aleatoria
𝑃 𝑦 = 𝐴2
|𝑛1 ≠ 𝑛2 = 𝑝2
+ 1 − 𝑝 2
= 2𝑝2
− 2𝑝 + 1
y
𝑃 𝑦 = −𝐴2
𝑛1 ≠ 𝑛2 = 2𝑝 1 − 𝑝 = 2𝑝 − 2𝑝2
Consecuentemente
𝑝 𝑦|𝑛1≠𝑛2
𝑌
= 2𝑝2 − 2𝑝 + 1 𝛿 𝑌 − 𝐴2 + 2𝑝 − 2𝑝2 𝛿 𝑌 + 𝐴2
Como
𝑅 𝑥 𝑡1, 𝑡2 = 𝐸 𝑥 𝑡1 𝑥 𝑡2 = 𝐸[𝑦]](https://image.slidesharecdn.com/7procesosestocasticos-190219132608/85/7-procesos-estocasticos-47-320.jpg)
![fasandoval@utpl.edu.ec
Onda Senoidal con Fase Aleatoria
• Considere el P.E. 𝑥(𝑡) definido por una señal sinosoidal
con un ángulo de fase aleatorio, o sea
𝑥 𝑡 = 𝐴 sin 2𝜋𝑓0 𝑡 + 𝜃
donde 𝜃 es una v.a. uniformemente distribuida en el
intervalo, (0, 2𝜋] o sea,
𝑝 𝜃 Θ = ቊ
12𝜋 ; Θ ∈ (0, 2𝜋]
0 ; Θ ∉ (0, 2𝜋]](https://image.slidesharecdn.com/7procesosestocasticos-190219132608/85/7-procesos-estocasticos-49-320.jpg)










![fasandoval@utpl.edu.ec
Densidad Espectral de Potencia
• En el caso de P.E.E.S.A., la densidad espectral de
potencia es dada por la transformada de su
función autocorrelación.
𝑆 𝑥 𝑓 = න
∞
∞
𝑅 𝑥 𝜏 𝑒−𝑗2𝜋𝑓𝜏
𝑑𝜏 = ℱ 𝑅 𝑥 𝜏
• La potencia media de un proceso 𝑥(𝑡) en una
banda de frecuencias caracterizadas por el
intervalo [𝑓1, 𝑓2] es dada por
𝑃𝑥 𝑓1,𝑓2
= න
−𝑓2
−𝑓1
𝑆 𝑥 𝑓 𝑑𝑓 + න
𝑓2
𝑓1
𝑆 𝑥 𝑓 𝑑𝑓](https://image.slidesharecdn.com/7procesosestocasticos-190219132608/85/7-procesos-estocasticos-60-320.jpg)

























![fasandoval@utpl.edu.ec
Referencias
• ALBUQUERQUE, J. P.A.; FORTES, J. M.; FINAMORE,W.A.
(1993) Modelos Probabilísticos em Engenharia Elétrica;
Rio de Janeiro: Publicação CETUC.
• Marco Grivet, Procesos Estocásticos I, Centro de Estudios
em Telecomunicaciones – CETUC, 2006. [Slide]
• Universidad de Cantabria, Teoría de la Probabilidad,Teoría
de la Comunicación, Curso 2007-2008. [Slide]
• ALBERTO LEON-GARCIA, Probability, Statistics, and
Random Processes For Electrical
Engineering, Third Edition, Pearson – Prentice Hall,
University of Toronto, 2008.](https://image.slidesharecdn.com/7procesosestocasticos-190219132608/85/7-procesos-estocasticos-86-320.jpg)
