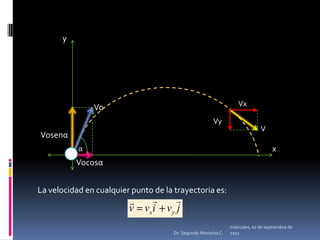
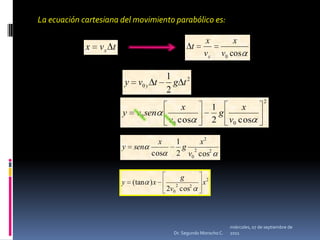
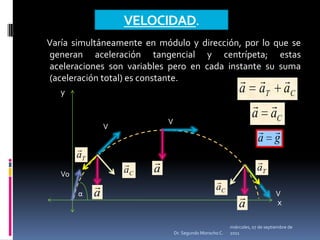
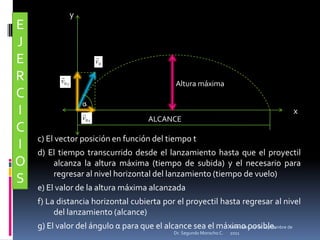
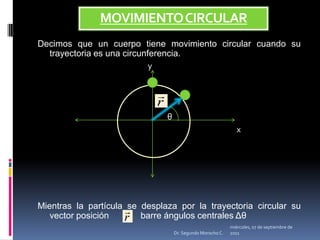
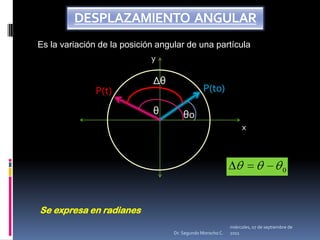
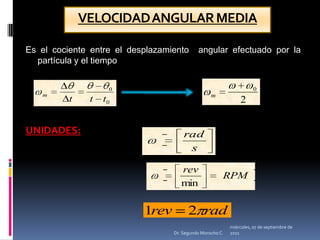
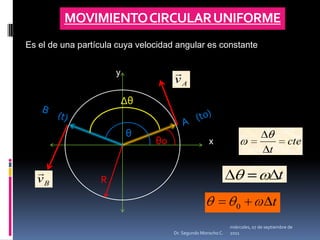
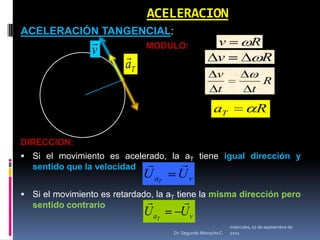
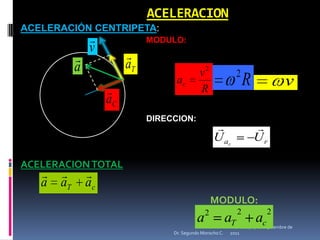
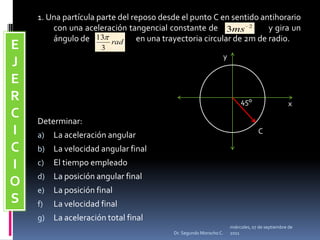
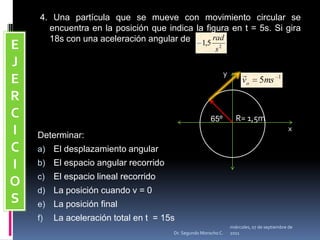
Este documento presenta información sobre diferentes tipos de movimiento, incluyendo movimiento parabólico, circular, circular uniforme y circular uniformemente variado. También incluye ecuaciones y ejemplos para calcular posición, velocidad, aceleración y otros parámetros para objetos en movimiento parabólico y circular. El documento concluye con una serie de ejercicios de aplicación.

1. UNIDAD 7 MOVIMIENTO EN EL PLANO7.1. Movimiento Parabólico7.2. Movimiento Circular7.3. Movimiento Circular Uniforme7.4. Movimiento Circular Uniformemente Variado miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

2. MOVIMIENTO PARABOLICOEs curvilíneo, plano, con trayectoria parabólica y aceleración total constante.Un ejemplo típico de éste movimiento es el lanzamiento de proyectiles, que tiene las siguientes características:La aceleración total es igual a la aceleración de la gravedadLa velocidad inicial no puede ser nulaLa dirección de la velocidad inicial es diferente a la de la aceleraciónmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

3. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.La posición de la partícula en cualquier punto de la trayectoria esta determinada por:El análisis del movimiento de un proyectil se realiza en función de su velocidad inicial. (α generalmente es un ángulo agudo) La velocidad inicial en función de sus componentes es:Y su dirección:

4. yVoVosenα xVocosαLa velocidad en cualquier punto de la trayectoria es:miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.VxVyVα

5. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.Como: se tiene: Igualando las componentes en x e y: El movimiento parabólico es compuesto, resulta de la suma simultáneade un MRU en el eje horizontal y un MRUV en el eje vertical.

6. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.En el eje horizontalEl en eje vertical Si α = 0 es un lanzamiento horizontal donde voy = 0En el eje horizontalEl en eje vertical

7. La ecuación cartesiana del movimiento parabólico es:miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

8. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.VELOCIDAD.Varía simultáneamente en módulo y dirección, por lo que se generan aceleración tangencial y centrípeta; estas aceleraciones son variables pero en cada instante su suma (aceleración total) es constante. y x VVVoαV

9. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.ACELERACION.Para cualquier posición la aceleración tangencial es la proyección de la aceleración total en la dirección de la velocidad.Por tanto:

10. 1. Desde lo alto de un edificio se dispara un proyectil con una velocidad de . Determinar a los 5s:La aceleración totalLa posición del cuerpoLa distancia recorrida horizontal y verticalmenteLa velocidad de la partículaLa aceleración tangencial y centrípeta2. Un cuerpo rueda por el tablero horizontal de una mesa de 1,55m de altura y abandona ésta con una velocidad de Determinar: A qué distancia del borde de la mesa, el cuerpo golpea el sueloLa posición del cuerpo cuando llega al sueloLa velocidad con que golpea contra el sueloLa aceleración total, tangencial y centrípeta en el momento de llegar al sueloEJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

11. 3. Una bola que rueda sobre una mesa horizontal de 75cm de altura cae tocando el suelo en un punto situado a una distancia horizontal de 1,5m del borde de la mesa. ¿Cuál era la velocidad de la bola en el momento de abandonar la mesa?4. Los peldaños de una escalera miden 12cm de altura y 30cm horizontalmente. Determinar:Cuál es la velocidad en dirección horizontal que debe comunicarse a una bola para que su primer rebote sea en la mitad del cuarto escalónQué velocidad tiene la bola en el instante del primer impacto5. Un jugador de tenis comunica a una bola una velocidad horizontal de módulo . La bola toca el suelo a una distancia de 20m del jugador. ¿ A qué altura fue golpeada la bola?6. Un proyectil es lanzado con una rapidez v0 y su dirección forma un ángulo α sobre la horizontal. Determinar:El vector velocidad inicialEl vector velocidad en función del tiempo tEJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

12. y xc) El vector posición en función del tiempo td) El tiempo transcurrido desde el lanzamiento hasta que el proyectil alcanza la altura máxima (tiempo de subida) y el necesario para regresar al nivel horizontal del lanzamiento (tiempo de vuelo)e) El valor de la altura máxima alcanzadaf) La distancia horizontal cubierta por el proyectil hasta regresar al nivel del lanzamiento (alcance)g) El valor del ángulo α para que el alcance sea el máximo posible.miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.Altura máximaEJERCICIOSαALCANCE

13. 7. Halle el ángulo α de lanzamiento para el cual el alcance es igual a la altura máxima. 8. Determine los ángulos de lanzamiento para los cuales el alcance de un proyectil sea 240m si la velocidad inicial tiene módulo 9. Un proyectil lanzado oblicuamente con un ángulo de 45° y una velocidad de cae a una distancia x del sitio de lanzamiento. Calcule la altura, si es disparado horizontalmente con la misma velocidad para que caiga en el mismo sitio. 10. Se lanza un proyectil desde el punto de coordenadas (4,3)m con una velocidad de . Determinar.La aceleración, velocidad y posición para cualquier tiempoEl tiempo de vueloEl alcance horizontalLa altura máximaLa velocidad del proyectil en 1sLa aceleración tangencial y la centrípeta en 1sEJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

14. 11. Una partícula parte del origen con una rapidez de en la dirección positiva del eje de las y. Su aceleración es constante e igual a . Determinar: La forma de la trayectoriaLa posición de la partícula para cualquier tiempo tLa velocidad de la partícula en t = 3sLa rapidez de la partícula en t = 3s12. Un jugador de golf comunica a su pelota una velocidad inicial horizontal de y una velocidad inicial vertical de . Escribir las ecuaciones cinemáticas del movimiento y calcular la altura máxima y el alcance de la pelota 13. Se lanza una pelota con una velocidad inicial de que hace un ángulo de 37° con la horizontal. Escribir las ecuaciones cinemáticas del movimiento y calcular la altura máxima y el alcance de la pelotaEJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

15. 14. Un jugador de básquetbol lanza desde el suelo la pelota con una velocidad inicial de que hace un ángulo de 53° con la horizontal. La canasta esta situada a 6m del jugador y tiene una altura de 3m. ¿Podrá encestar?15. Un futbolista comunica a una pelota una velocidad de con dirección de 37° con la horizontal. Encontrándose a 8m de distancia del arco de 2,5m de altura. ¿Habrá posibilidad de gol? 16. Una pelota de béisbol abandona el bate a una altura de 1,20m sobre el suelo, formando un ángulo de 45° con la horizontal y con una velocidad inicial tal que el alcance horizontal hubiera sido de 120m. A los 108m de distancia desde la plataforma del lanzamiento se encuentra una valla de 9m de altura. ¿Pasará la pelota por encima de la valla?EJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

16. 17. Un proyectil es disparado formando un ángulo de tiro igual a 60° y choca contra un edificio situado a 24m del punto del disparo en un punto del edificio situado a 14,4m por encima de la proyección del lanzamiento. Calcular: a) La velocidad inicial el proyectilb) La velocidad al momento del impacto c) La dirección que tiene el proyectil al momento del impactoEJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

17. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.MOVIMIENTO CIRCULARDecimos que un cuerpo tiene movimiento circular cuando su trayectoria es una circunferencia. y θ x Mientras la partícula se desplaza por la trayectoria circular su vector posición barre ángulos centrales Δθ

18. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.POSICION ANGULAREs el ángulo θ que existe entre el vector posición de la partícula y el eje x y θ x El ángulo θ generalmente se expresa en radianes

19. NOTA 1. Todo ángulo medido en grados se puede convertir a radianes multiplicando por: NOTA 2. Todo ángulo medido en radianes se puede convertir a grados multiplicando por: Convertir en radianes:30º45º60º90º180º270º360ºConvertir en grados:miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

20. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.DESPLAZAMIENTO ANGULAREs la variación de la posición angular de una partícula y x Se expresa en radianesΔθP(to)P(t)θθo

21. VELOCIDAD ANGULAR MEDIAEs el cociente entre el desplazamiento angular efectuado por la partícula y el tiempoUNIDADES:miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

22. ACELERACION ANGULARCociente entre la variación de la velocidad angular que experimenta una partícula y el intervalo de tiempo en que se produjoUNIDADESmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

23. Una partícula parte del punto (-3,4) cm, moviéndose en sentido antihorario sobre una trayectoria circular con centro en el origen, con una velocidad angular constante de . DeterminarLa posición angular inicialEl desplazamiento angular en 10sLa posición angular finalLa posición final 2. Una partícula gira por una trayectoria circular con una velocidad angular constante de . Determinar:El tiempo necesario para girar un ángulo de 620°El tiempo necesario para dar 12 revolucionesEl ángulo (en grados) girado en 9sEl número de vueltas que da en 2min.EJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

24. 3. Una partícula animada de movimiento circular parte del punto (5,-2) cm en sentido antihorario con una velocidad angular de y se mueve durante 5s con una aceleración angular de . Determinar:La velocidad angular finalLa velocidad angular mediaEl desplazamiento angularLa posición angular inicialLa posición finalEJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

25. MOVIMIENTO CIRCULAR UNIFORMEEs el de una partícula cuya velocidad angular es constante y xmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.ΔθB (t)A (to)θθoR

26. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.El móvil recorre arcos iguales en tiempos iguales (todas las vueltas serán recorridas en tiempos iguales)PERIODO (T) Tiempo empleado en recorrer una vuelta completa Si Δθ = 2πrad entonces Δt = T; por tanto:UNIDADES

27. FRECUENCIA (f)Es el número de revoluciones por unidad de tiempoUNIDADESDISTANCIA (d)Es la longitud del arco que se determina por:miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

28. ACELERACION CENTRIPETA Si ω es cte entonces v = cte; por lo tanto aT = 0La variación en la dirección genera acMóduloDirección Hacia el centro de la trayectoria, opuesta a la de la posición y perpendicular a la velocidadmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

29. 1. Una Partícula que se mueve por una trayectoria circular de 1,6m de radio, gira un ángulo de 125° cada 7s. Determinar:La velocidad angular de la partículaLa rapidez de la partículaEl períodoLa frecuenciaEl módulo de la aceleración centrípeta.2. Una partícula da 415 RPM en una circunferencia de 1,2m de radio. Determinar:Su velocidad angularSu períodoLa rapidez de la partículaEl módulo de la aceleración centrípetaLa distancia recorrida en 5sEJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

30. 3. Un cuerpo parte del punto (-2,6) m y gira en sentido antihorario a 500RPM durante 4s. Si el centro de la circunferencia esta en el origen, determinar: La velocidad angularLa posición angular inicialLa posición angular finalLa posición finalCuántas vueltas da en los 4sEl períodoLa velocidad en la posición inicialLa aceleración centrípeta en la posición finalEJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

31. 4. Una partícula animada de MCU se encuentra en la posición que indica la figura en t = 3s. Si se mueve en sentido horario 7s, determinar:La velocidad angularEl desplazamiento angularCuántas vueltas da en los 7sLa distancia recorridaLa posición finalEl períodoLa velocidad en t = 10sLa aceleración centrípeta en t = 3sEJERCICIOSmiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

32. MOVIMIENTO CIRCULAR UNIFORMEMENTE VARIADOEs el de una partícula cuya aceleración angular es constante. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

33. Recordando las expresiones para la velocidad media:miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

34. Por otro lado:Si el movimiento es acelerado ω y α tienen signos iguales (mismo sentido de giro)Si el movimiento es retardado ω y α tienen signos opuestos (distinto sentido de giro)miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

35. ACELERACIONACELERACIÓN TANGENCIAL: MODULO:DIRECCION: Si el movimiento es acelerado, la aT tiene igual dirección y sentido que la velocidad Si el movimiento es retardado, la aT tiene la misma dirección pero sentido contrariomiércoles, 04 de mayo de 2011Dr. Segundo Morocho C.

36. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.ACELERACIONACELERACIÓN CENTRIPETA: MODULO:DIRECCION:ACELERACION TOTAL MODULO:

37. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.1. Una partícula parte del reposo desde el punto C en sentido antihorario con una aceleración tangencial constante de y gira un ángulo de en una trayectoria circular de 2m de radio. Determinar: La aceleración angularLa velocidad angular finalEl tiempo empleadoLa posición angular finalLa posición finalLa velocidad finalLa aceleración total finaly45ºxEJERCICIOSC

38. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.2. Un cuerpo que esta girando por una trayectoria circular de 0,75m de radio, demora 3s en girar un ángulo de y alcanza una velocidad angular de 50RPM. Determinar: La velocidad angular mediaLa velocidad angular inicialLa aceleración angularLa rapidez inicialLa rapidez finalLa distancia recorridaEJERCICIOS

39. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C.3. Una partícula se mueve en la trayectoria circular de la figura. Si parte del punto A con una rapidez de y, luego de girar un ángulo de , llega al punto B con una rapidez de Determinar:La velocidad angular inicial y finalLa aceleración angularEl tiempo transcurridoLa posición angular finalLa posición finalLa velocidad finalLa aceleración total finalyR= 1,3m40ºxEJERCICIOS

40. miércoles, 04 de mayo de 2011Dr. Segundo Morocho C. 4. Una partícula que se mueve con movimiento circular se encuentra en la posición que indica la figura en t = 5s. Si gira 18s con una aceleración angular de Determinar:El desplazamiento angular El espacio angular recorridoEl espacio lineal recorrido La posición cuando v = 0La posición finalLa aceleración total en t = 15syR= 1,5mEJERCICIOS65ºx