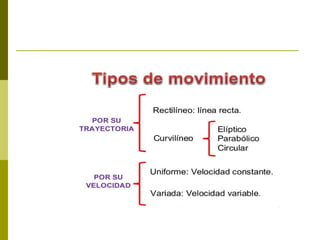
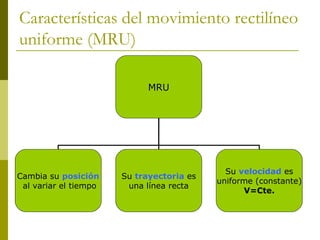
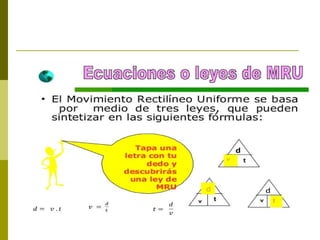
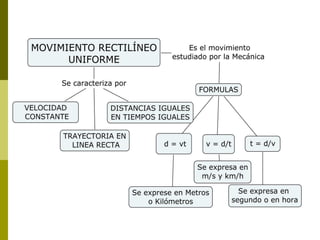
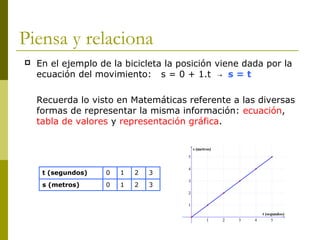
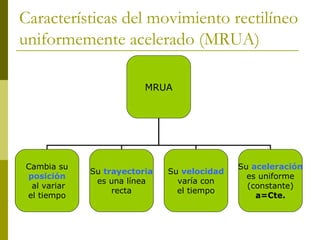
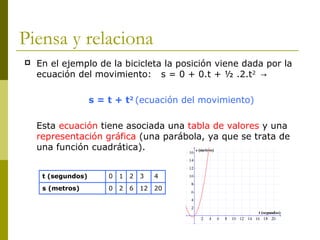
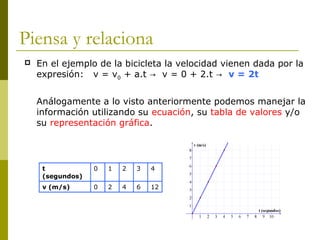
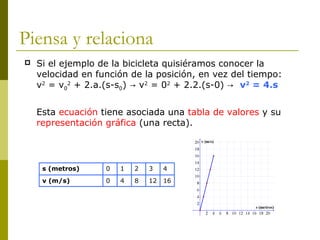
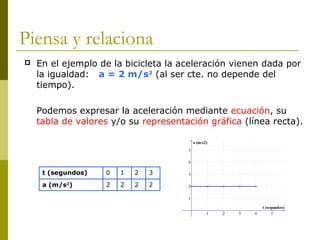
Este documento describe los tipos de movimiento rectilíneo: movimiento rectilíneo uniforme (MRU) y movimiento rectilíneo uniformemente acelerado (MRUA). El MRU se caracteriza por una velocidad constante, mientras que el MRUA se caracteriza por una aceleración constante que hace que la velocidad cambie con el tiempo. El documento proporciona ecuaciones matemáticas para describir la posición, velocidad y aceleración en función del tiempo para cada tipo de movimiento.

1. Movimientos
rectilíneos
Movimiento rectilíneo uniforme (MRU)
Y
Movimiento rectilíneo uniformemente
acelerado (MRUA)

5. ¿Qué es un movimiento rectilíneo?
 Es aquel que tiene un cuerpo, un móvil, que cumple las
siguientes propiedades:
 Cambia su posición al avanzar el tiempo, es decir, se
está moviendo.
 Su trayectoria, el camino o la ruta que sigue es una
línea recta.
Ejemplo: un coche en un tramo recto de una autopista, el
ascensor de un edificio o un corredor de 100 metros
lisos.

7. MRU: Movimiento Rectilíneo Uniforme
 La principal característica del movimiento rectilíneo
uniforme es que su velocidad es constante, y por tanto
recorre el mismo espacio cada segundo que se mueve. ¿Te
acuerdas de las funciones en matemáticas?. Piensa en el
ejemplo de la bolsa de Chaskis: 1 bolsa cuesta 0,30€; 2
bolsas 0,60€; 3 bolsas 0,90€…
 Imagínate pedaleando en tu bicicleta a un ritmo constante:
en 1 seg. recorres 1 metro, en 2 seg. 2 metros... ¿Cuántos
metros recorres cada segundo? Exacto: 1 metro cada
segundo, es decir, v=1m/s. ¡Esto es un MRU!

8. Características del movimiento rectilíneo
uniforme (MRU)
MRU
Cambia su posición
al variar el tiempo
Su trayectoria es
una línea recta
Su velocidad es
uniforme (constante)
V=Cte.

9. Ecuaciones de un MRU
 s = so + v.t (Ecuación del movimiento) siendo:
- s: Posición final (m) para un determinado t.
- v: Velocidad (m/s)
- t: Tiempo (s)
 Por tanto, s me dice dónde está el móvil en un determinado
momento t.
 En nuestro ejemplo anterior para t=1s. s=1m; para t=2s.→
s=2m; etc.→

13. Piensa y relaciona
t (segundos) 0 1 2 3
s (metros) 0 1 2 3
 En el ejemplo de la bicicleta la posición viene dada por la
ecuación del movimiento: s = 0 + 1.t → s = t
Recuerda lo visto en Matemáticas referente a las diversas
formas de representar la misma información: ecuación,
tabla de valores y representación gráfica.

14. Sigue pensando y relacionando…
t (segundos) 0 1 2 3
v (m/s) 1 1 1 1
 En el ejemplo de la bicicleta la velocidad vienen dada por la
expresión: v = 1 m/s (al ser cte. no depende del tiempo)
Análogamente a lo visto anteriormente podemos manejar la
información utilizando su ecuación, su tabla de valores y/o
su representación gráfica (una línea recta).

15. MRUA: Movimiento Rectilíneo
Uniformemente Acelerado
 La principal característica del movimiento rectilíneo
uniformemente acelerado es que su aceleración es
constante, y por tanto se mueve más rápido (con mayor
velocidad) cada segundo que pasa.
 Imagínate pedaleando en tu bici persiguiendo a otro ciclista
que va más rápido que tú. Debes aumentar tu velocidad
para llegar a él: en 1 segundo vas a 3 m/s, en 2 segundos
a 5 m/s, en 3 segundos a 7 m/s... ¿Cuánto aumenta tu
velocidad cada segundo? Exacto: 2 metros cada segundo,
es decir, a=2 m/s2
. ¡Esto es un MRUA!

16. Características del movimiento rectilíneo
uniformemente acelerado (MRUA)
MRUA
Cambia su
posición
al variar
el tiempo
Su trayectoria
es una línea
recta
Su aceleración
es uniforme
(constante)
a=Cte.
Su velocidad
varía con
el tiempo

17. Ecuaciones de un MRUA (I)
 s = so + vo.t + ½ a.t2
(ecuación del movimiento) siendo:
- s : Posición final (m) para un determinado t.
- so: Posición inicial (m)
- vo: Velocidad inicial (m/s)
- a : Aceleración (m/s2
)
- t : Tiempo (s)
 Por tanto, s me dice dónde está el móvil en un determinado
momento t.

18. Piensa y relaciona
t (segundos) 0 1 2 3 4
s (metros) 0 2 6 12 20
 En el ejemplo de la bicicleta la posición viene dada por la
ecuación del movimiento: s = 0 + 0.t + ½ .2.t2
→
s = t + t2
(ecuación del movimiento)
Esta ecuación tiene asociada una tabla de valores y una
representación gráfica (una parábola, ya que se trata de
una función cuadrática).

19. Ecuaciones de un MRUA (II)
 v = vo + a.t (ecuación de la velocidad) siendo:
- v : Velocidad (m/s)
- vo: Velocidad inicial (m/s)
- a : aceleración (m/s2
)
- t : Tiempo (s)
 Por tanto, la ecuación me dice cuál es la velocidad v del
móvil en un determinado momento t.

20. Piensa y relaciona
t
(segundos)
0 1 2 3 4
v (m/s) 0 2 4 6 12
 En el ejemplo de la bicicleta la velocidad vienen dada por la
expresión: v = v0 + a.t v = 0 + 2.t→ → v = 2t
Análogamente a lo visto anteriormente podemos manejar la
información utilizando su ecuación, su tabla de valores y/o
su representación gráfica.

21. Ecuaciones de un MRUA (III)
 v2
= vo
2
+ 2.a.(s- so) , siendo:
- s : Posición final (m) para un determinado t.
- so: Posición inicial (m)
- v : Velocidad (m/s)
- vo: Velocidad inicial (m/s)
- a : aceleración (m/s2
)
 Esta ecuación nos dice cuál es la velocidad v del móvil en
una determinada posición s.

22. Piensa y relaciona
s (metros) 0 1 2 3 4
v (m/s) 0 4 8 12 16
 Si el ejemplo de la bicicleta quisiéramos conocer la
velocidad en función de la posición, en vez del tiempo:
v2
= v0
2
+ 2.a.(s-s0) v→ 2
= 02
+ 2.2.(s-0) → v2
= 4.s
Esta ecuación tiene asociada una tabla de valores y su
representación gráfica (una recta).

23. Piensa y relaciona
t (segundos) 0 1 2 3
a (m/s2
) 2 2 2 2
 En el ejemplo de la bicicleta la aceleración vienen dada por
la igualdad: a = 2 m/s2
(al ser cte. no depende del
tiempo).
Podemos expresar la aceleración mediante ecuación, su
tabla de valores y/o su representación gráfica (línea recta).