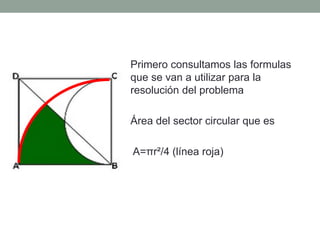
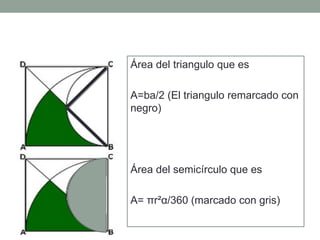
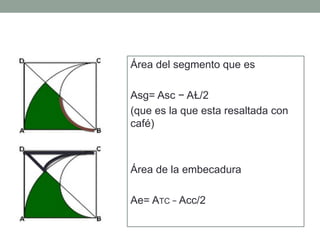
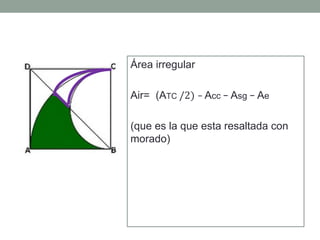
Este documento presenta la resolución de un problema de razonamiento matemático para calcular el área de una sección irregular que será construida para una área recreativa. Primero se identifican las fórmulas para calcular el área de figuras como sectores circulares, triángulos, segmentos y semicírculos. Luego, se aplican sucesivamente estas fórmulas para hallar el área de cada sección y subsección hasta obtener el área total irregular de 515.555 m2.

1. PROBLEMA DE RAZONAMIENTO
MATEMÁTICO
Mariana Ramírez García 2 «C»

2. Problema de razonamiento
Área recreativa que se va a construir al oriente de la
ciudad.

3. Primero consultamos las formulas
que se van a utilizar para la
resolución del problema
Área del sector circular que es
A=πr²/4 (línea roja)

4. Área del triangulo que es
A=ba/2 (El triangulo remarcado con
negro)
Área del semicírculo que es
A= πr²α/360 (marcado con gris)

5. Área del segmento que es
Asg= Asc − AⱢ/2
(que es la que esta resaltada con
café)
Área de la embecadura
Ae= ATC − Acc/2

6. Área irregular
Air= (ATC /2) − Acc − Asg − Ae
(que es la que esta resaltada con
morado)

7. Resolucion
Primero sacamos el área del sector circular que es
Acc= πr²/4
Acc= 3.1416 (85²)/4
Acc= 5674.515 m²
Posteriormente se calculo el área del triangulo
AⱢ= ba/2
AⱢ= (85)(425)/2
AⱢ= 1806.25 m²

8. • Después se saco el área del segmento del circulo de esta
forma
Asg= Asc − AⱢ/2
Asg= (2837.2575 − 1806.25)/2
Asg= 515.5037 m²
• A continuación obtendremos el área de la figura a la que
llamamos «embecadura»
Ae= ATC − Acc/2
Ae= 7225 − 5674.515/2
Ae= 515.555 m²

9. • Después vamos a sacar el área de la figura irregular que
es del siguiente modo
Air= (ATC/2) − AⱢ − Acc − Asg − Ae
Air= (7225/2) − 1806.25 − 515.5037 − 515.555
Air= 3612.5 − 515.5037 − 775.2491345
Air= 515.555 m²

10. • Av= (ATC/2) − Ae −Air
• Av= (7225/2) − 775.2491345 − 515.555
• Av= 2837.2508866 − 515.555
Av= 2321.695866