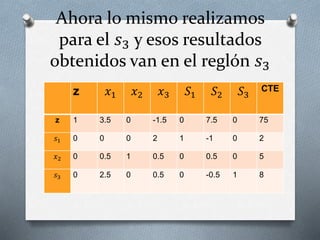
El método simplex se utiliza para resolver problemas de programación lineal maximizando una función objetivo sujeto a restricciones. El resumen describe los pasos del método simplex para determinar la cantidad óptima de cada tipo de cuadro que una empresa debe fabricar para maximizar sus ganancias, sujeto a los recursos disponibles de madera, cristal y pintura. El método simplex conduce a una solución óptima de fabricar 3 unidades del primer cuadro, 3 unidades del segundo cuadro y 1 unidad del tercer cuadro, maximizando la utilidad en $87.

1. MÉTODO
SIMPLEX

2. Requisitos:
O 1- Todas las restricciones deben estar
establecidas como ecuaciones.
O 2- El segundo miembro No debe ser
negativo.
O 3- Todas las variables están restringidas a
valores No negativos.

3. Condiciones:
≤ Se aumenta una variable
positiva de holgura 𝑠𝑗
≥
Se aumenta una variable
negativa de holgura 𝑠𝑗 mas una
variable artificial 𝑀𝑗 positiva.
Por condiciones de No
negatividad, se aumenta
una variable artificial𝑀𝑗
=

4. Problema
O Una empresa se dedica al armado de
cuadros decorativos, para ello se cuentan
con los siguientes recursos y procesos:
Madera Cristal Pintura Utilidad
Cuadro 1 1 1 3 $11
Cuadro 2 2 2 1 $15
Cuadro 3 3 1 1 $9
Disponible 12 10 13

5. Determinar la cantidad de
cada tipo de cuadro que deberá
fabricar para alcanzar una
máxima utilidad:
OEl modelo sería:
O𝑥1 = 𝑐𝑎𝑛𝑡𝑖𝑑𝑎𝑑 𝑑𝑒 𝑐𝑢𝑎𝑑𝑟𝑜𝑠 1
O𝑥2 = 𝑐𝑎𝑛𝑡𝑖𝑑𝑎𝑑 𝑑𝑒 𝑐𝑢𝑎𝑑𝑟𝑜𝑠 2
O𝑥3 = 𝑐𝑎𝑛𝑡𝑖𝑑𝑎𝑑 𝑑𝑒 𝑐𝑢𝑎𝑑𝑟𝑜𝑠 3
OMaximar
O𝑍 = 11𝑥1 + 15 𝑥2 + 9 𝑥3

6. Sujeto a
O1𝑥1 + 2𝑥2 + 3𝑥3 ≤ 12
O1𝑥1 + 2𝑥2 + 1𝑥3 ≤ 10
O3𝑥1 + 1𝑥2 + 1𝑥3 ≤ 13
Condiciones No negatividad:
𝑥1, 𝑥2, 𝑥3 ≥ 0

7. Forma canónica
O𝑧 − 11𝑥1 − 15𝑥2 − 9𝑥3 = 0
O1𝑥1 + 2𝑥2 + 3𝑥3 + 𝑠1 = 12
O1𝑥1 + 2𝑥2 + 1𝑥3 + 𝑠2 = 10
O3𝑥1 + 1𝑥2 + 1𝑥3 + 𝑠3 = 13
OVariable de holgura

8. Elegimos la columna con el
valor mas negativo
z 𝑥1 𝑥2 𝑥3 𝑆1 𝑆2 𝑆3 CTE
z 1 -11 -15 -9 0 0 0 0
𝑠1 0 1 2 3 1 0 0 12
𝑠2 0 1 2 1 0 1 0 10
𝑠3 0 3 1 1 0 0 1 13
Elegimos lla columna con el valor mas negativo

9. Luego determinamos el lugar
que va a ocupar dividiendo el
resultado de las ecuaciones
entre los valores de la columna
elegida quedando:
O
12
2
= 6
O
10
2
= 5
O
13
1
= 13

10. Tomo el valor mas pequeño obtenido y es el
de 𝑠2 entonces 𝑥2va a entrar y 𝑠2 va a salir.
Completamos la tabla utilizando el método de
Gauss Jordan.
El pivote elegido es donde se cruzan la fila y
columna elegida, en este caso es el 2. Debe
ser 1 el pivote, entonces divido entre 2 todos
los elementos de esa fila.

11. O Se obtiene:
z 𝑥1 𝑥2 𝑥3 𝑆1 𝑆2 𝑆3 CTE
z
𝑠1
𝑥2 0 0.5 1 0.5 0 0.5 0 5
𝑠3

12. Multiplicar el reglón pivote por
el dato a eliminar en cada
reglón pero de signo contrario.
O En el caso de z se deberá multiplicarse tal pivote
por 15 luego sumarse con z para llenar el nuevo
espacio de z
O 15 𝑥2 →
15 0 15 0,5 15 1 15 0,5 15 0 15 0,5 15 0 15 5
O Ese resultado se suma con el valor de Z
O
0 7.5 15 7.5 0 7.5 0 75
1 -11 -15 -9 0 0 0 0
1 3.5 0 1.5 0 7.5 0 75

13. Y los valores obtenidos van en
el lugar de la fila z
z 𝑥1 𝑥2 𝑥3 𝑆1 𝑆2 𝑆3 CTE
z 1 3.5 0 -1.5 0 7.5 0 75
𝑠1
𝑥2 0 0.5 1 0.5 0 0.5 0 5
𝑠3

14. En 𝑠1se requiere quitar el 2,
entonces multiplizamos el
pivote por -2
O −2 𝑥2 → −2 0 − 2 0,5 − 2 1
−2 0,5 − 2 0 − 2 0,5 − 2 0 − 2 5
O Ese resultado se suma con el valor de 𝑠1
0 -1 -2 -1 0 -1 0 -10
0 1 2 3 1 0 0 12
0 0 0 2 1 -1 0 2

15. Y esos resultados van en la fila
de 𝑠1de la tabla:
z 𝑥1 𝑥2 𝑥3 𝑆1 𝑆2 𝑆3 CTE
z 1 3.5 0 -1.5 0 7.5 0 75
𝑠1 0 0 0 2 1 -1 0 2
𝑥2 0 0.5 1 0.5 0 0.5 0 5
𝑠3

16. Ahora lo mismo realizamos
para el 𝑠3 y esos resultados
obtenidos van en el reglón 𝑠3
z 𝑥1 𝑥2 𝑥3 𝑆1 𝑆2 𝑆3
CTE
z 1 3.5 0 -1.5 0 7.5 0 75
𝑠1 0 0 0 2 1 -1 0 2
𝑥2 0 0.5 1 0.5 0 0.5 0 5
𝑠3 0 2.5 0 0.5 0 -0.5 1 8

17. Para saber si se debe continuar
hay que mirar la fila 2, como
hay numeros negativos hay
que segurir repitiendo el
proceso.
O Se elige la comumna con el valor negativo
mas grande y luego dividir los resultados de
la última columna entre los valores de la
columna elegida, para usar el reglón donde
se obtuvo el menor resultado.
O
2
0
= 𝑖𝑛𝑑𝑒𝑡𝑒𝑟𝑚𝑖𝑛𝑎𝑑𝑜
5
0,5
= 10
O
8
2,5
= 3,2

18. Por lo tanto 𝑥1va a entrar en el
reglón de 𝑠3 y el pivote va a ser
el valor 2,5
z 𝑥1 𝑥2 𝑥3 𝑆1 𝑆2 𝑆3 CTE
z 1 0 0 -0.8 0 6.8 1.4 86.2
𝑠1 0 0 0 2 1 -1 0 2
𝑥2 0 0 1 0.4 0 0.6 -0.2 3.4
𝑥1 0 1 0 0.2 0 -0.2 0.4 3.2

19. Sigue habiendo un valor
negativo en z, se debe volver a
repetir el proceso, tomando
esa columna 𝑥3 entre los
valores 𝑠1
O
2
2
= 1
3,4
0,4
= 8,5
O
3,2
0,2
= 16
O Y tomar el de valor menor, en este caso
2/2= 1
O Dividiendo todos los valores del reglón
𝑠1 entre 2

20. Quedando la tabla:
z 𝑥1 𝑥2 𝑥3 𝑆1 𝑆2 𝑆3 CT
E
z
𝑥3 0 0 0 2 1 0.5 -0.5 1
𝑥2
𝑥1

21. Lo mismo con el 𝑥3para -0,2 y
se completa la tabla de la
siguiente manera:
z 𝑥1 𝑥2 𝑥3 𝑆1 𝑆2 𝑆3 CTE
z 1 0 0 0 0.4 6.4 1.4 87
𝑥3 0 0 0 1 0.5 -0.5 0 1
𝑥2 0 0 1 0 -0.2 0.8 -0.2 3
𝑥1 0 1 0 0 -0.1 -0.1 0.4 3

22. Ahora no tenemos ningún
valor negatico en z, entonces
hemos terminado y el valor de
la última columna en z, nos
dice que se maximiza en 𝑧 =
87
Cuando 𝑥1 = 3
𝑥2 = 3 𝑦 𝑥3 = 1