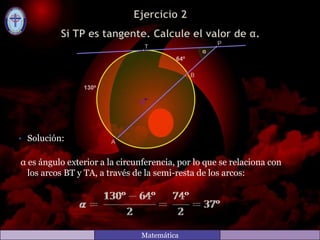
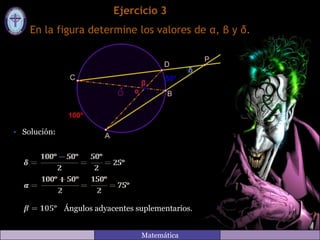
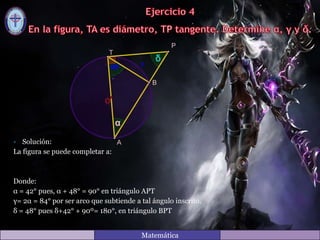
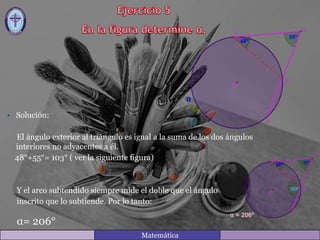
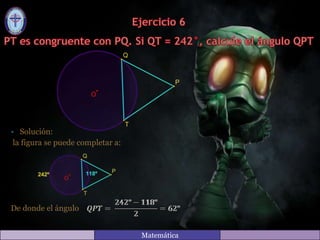
Este documento contiene las soluciones a varios ejercicios de matemáticas relacionados con ángulos y arcos en figuras geométricas. Cada solución explica cómo calcular los valores de los ángulos utilizando propiedades como la suma de los ángulos interiores de un triángulo, la relación entre ángulos y arcos en una circunferencia, y ángulos adyacentes suplementarios.

1. Ejercicios resueltos

2. • Solución:
δ es ángulo exterior a la circunferencia, por lo que se
relaciona con los arcos α y β, a través de la semi-resta de los
arcos:
Matemática

3. Matemática
• Solución:
α es ángulo exterior a la circunferencia, por lo que se relaciona con
los arcos BT y TA, a través de la semi-resta de los arcos:

4. Ejercicio 3
En la figura determine los valores de α, β y δ.
• Solución:
Ángulos adyacentes suplementarios.
Matemática

5. • Solución:
La figura se puede completar a:
Donde:
α = 42° pues, α + 48° = 90° en triángulo APT
γ= 2α = 84° por ser arco que subtiende a tal ángulo inscrito.
δ = 48° pues δ+42° + 90º= 180°, en triángulo BPT
Matemática

6. • Solución:
El ángulo exterior al triángulo es igual a la suma de los dos ángulos
interiores no adyacentes a él.
48°+55°= 103° ( ver la siguiente figura)
Y el arco subtendido siempre mide el doble que el ángulo
inscrito que lo subtiende. Por lo tanto:
α= 206°
Matemática

7. • Solución:
la figura se puede completar a:
De donde el ángulo
Matemática

8. • Solución:
X es ángulo exterior a la circunferencia y su medida queda
determinada por:
Matemática

9. • Solución:
X es ángulo exterior del triángulo, por lo tanto,
equivale a la suma d los dos ángulos interiores
no adyacentes a el.
X= α + γ = 21° + 63° = 84°
Matemática

10. Matemática