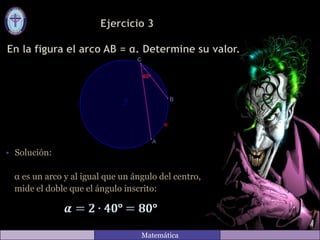
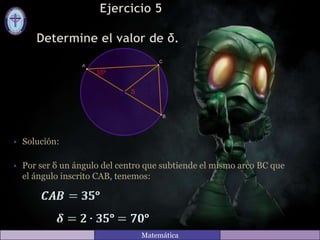
El documento contiene varias soluciones de ejercicios de matemáticas relacionados con ángulos y arcos. Explica que los ángulos del centro miden el doble que los ángulos inscritos que subtienden el mismo arco y que los ángulos inscritos miden la mitad del arco que subtienden. También calcula valores numéricos de ángulos en diferentes figuras geométricas como triángulos y círculos.

1. Ejercicios resueltos

2. Matemática

3. ▫ Solución:
α es un ángulo del centro y por lo tanto, mide el doble
que el ángulo inscrito que subtiende el mismo arco de
la circunferencia que el.
Matemática

4. • Solución:
α es un arco y al igual que un ángulo del centro,
mide el doble que el ángulo inscrito:
Matemática

5. Ejercicio 4
En la siguiente figura, calcule α, β y δ.
• Solución:
• α es un ángulo del centro y por lo tanto , mide el doble que el ángulo
inscrito que subtiende el mismo arco, es decir:
• α y β son ángulos inscritos que subtienden el mismo arco que el ángulo
de 48°. Por lo tanto, miden lo mismo que este. Es decir:
Matemática

6. • Solución:
• Por ser δ un ángulo del centro que subtiende el mismo arco BC que
el ángulo inscrito CAB, tenemos:
Matemática

7. • Solución:
• α es un ángulo inscrito, por lo tanto, mide la mitad
que el arco que subtiende:
Matemática

8. • Solución:
Cada vértice del triángulo equilátero divide los 360° de la
circunferencia en tres arcos y ángulos del centro congruentes (de igual
medida).
Es decir,
Mientras,
Matemática

9. • Solución:
Como OA = OC = r, los ángulos que se oponen a tales lados son iguales
(ángulos basales) y miden 37°. En este caso:
Ángulos OAC = ACO = 37°
Y el arco α es igual al ángulo del centro del triángulo AOC. Este último
se puede deducir mediante la suma de los ángulos interiores en todo
triángulo ( 180°)
Matemática

10. Matemática