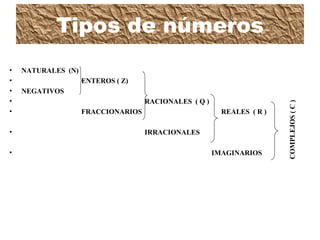
El documento describe los diferentes tipos de números y sus propiedades. Explica que los números naturales surgieron de la necesidad de contar y que los números enteros incluyen tanto números positivos como negativos. También cubre conceptos como la suma, resta, multiplicación y división de números enteros, incluyendo la jerarquía de operaciones y el uso de paréntesis.

1. ESPAD III * TC 1 NUMEROS NATURALES Y NÚMEROS ENTEROS

2. Tipos de números NATURALES (N) ENTEROS ( Z) NEGATIVOS RACIONALES ( Q ) FRACCIONARIOS REALES ( R ) IRRACIONALES IMAGINARIOS COMPLEJOS ( C )

3. Función y utilidad de los números. Los números permiten: CONTAR  Números cardinales ORDENAR  Números ordinales IDENTIFICAR Y además.... EXPRESAR MEDIDAS  Medir CALCULAR  Aritmética

4. LOS NÚMEROS NATURALES Origen de los números naturales Los números naturales surgen por la necesidad de contar. Tal y como se conocen hoy en día , los números naturales son: 0, 1, 2, 3, 4... Se representan con la letra N. El sistema de numeración decimal Es un sistema que sirve para expresar cualquier número. En él se utilizan diez cifras: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 A estas cifras se les llama cifras arábigas, porque fueron introducidas por los árabes. Cada cifra fue elegida según el número de ángulos que tenía su grafo original:

5. CRITERIOS DE DIVISIBILIDAD 8.195 Todo número en el cual el valor absoluto de la diferencia de la suma de las cifras de lugar par e impar sea múltiplo de 11 11 12.780 Todo número que termine en 0. 10 7.578 Todo número cuya suma de sus cifras sea múltiplo de 9 9 13.720 Todo número cuyas tres últimas cifras formen un múltiplo de 8 8 476 (  35) Todo número que al suprimir la cifra de las unidades y restar del número que queda el doble de la cifra suprimida, se obtenga un múltiplo de 7 7 312 Todo número múltiplo de 2 y de 3 a la vez 6 315 Todo número que termine en 0 o en 5 5 2512 Todo número cuyas dos últimas cifras formen un múltiplo de 4 4 321 Todo número cuya suma de sus cifras sea múltiplo de 3 3 312 Todos los números terminados en 0 o en cifra par 2 CRITERIOS DE DIVISIBILIDAD POR:

6. NÚMEROS ENTEROS Un número entero a es menor que otro b, si para pasar del número a al número b hay que añadirle una o más unidades. Se escribe a < b Ejemplo 1 2 < 5  Al 2 hay que añadirle 3 unidades para llegar al 5. Ejemplo 2 - 2 < 3  Al - 2 hay que añadirle 5 unidades para llegar al 3.

7. Un número entero a es mayor que otro b, si para pasar del número a al número b hay que quitarle una o más unidades. Se escribe a > b Ejemplo 1 5 > 2  Al 5 hay que quitarle 3 unidades para llegar al 2. Ejemplo 2 2 > - 3  Al 2 hay que quitarle 5 unidades para llegar al - 3. Ejemplo 3 - 2 > - 5  Al - 2 hay que quitarle 3 unidades para llegar al - 5.

8. USO DE NÚMEROS ENTEROS USOS Hay situaciones que se pueden expresar matemáticamente utilizando sólo los números naturales . Ejemplos : Edad de una persona, número de hijos de una familia, número de viviendas en un barrio, etc. Pero hay otras situaciones en que aparecen cantidades que necesitan un sentido, y que se representan con los números positivos y negativos . Ejemplos: Ganar o perder dinero, tener o deber. Temperatura por encima o por debajo de 0ºC. Tiempo después de Cristo o antes de Cristo. Alturas de una vivienda o sótanos. El conjunto de números positivos ( N , naturales) y números negativos son los números enteros ( Z ).

9. LOS NÚMEROS NEGATIVOS Se expresan con un – delante Ejemplo: – 5 Los + están por encima de cero, y los – por debajo de cero. Ejemplo: – 5 < 0 ; + 7 > 0 El cero no es ni + ni – Ejemplo: 0 ; + 0  Mal ; – 0  Mal Cuando se opera con – deberán ir entre paréntesis Ejemplo: 5 + (– 3) Cuando el nº es + no se pone signo. Ejemplo: – 5 = – 5 ; + 9 = 9 ; + 13 = 13

10. Sea la expresión: A = 2 + (-3) + 4 + (-5) + (-6) + 7 + 8 Los paréntesis que hay en ella no son tales. Es una manera de indicar que son números enteros negativos. No se pueden poner dos signos seguidos: 2 + - 3 Resolvemos: Se escriben todos los números aplicando la regla de los signos: A = 2 – 3 + 4 – 5 – 6 + 7 + 8 Y finalmente se opera de izquierda a derecha ; o se suman por un lado todos los positivos y por otro lado todos los negativos, restándose ambas sumas: A = (2 + 4 + 7 + 8 ) – ( 5 + 6) = 21 – 11 = 10 Sumas y diferencias SIN PARÉNTESIS

11. Otro ejemplo: Sea la expresión: B = 3 - (-2) + 7 - (-5) + (- 4) + 1 + 8 Resolvemos: Se escriben todos los números aplicando la regla de los signos: B = 3 + 2 + 7 + 5 – 4 + 1 + 8 B = (3 + 2 + 7 + 5 + 1 + 8 ) – ( 4) = 26 – 4 = 22

12. Sea la expresión: A = 2 + ( 3 – 4 ) + 1 – ( - 5 + 6 – 7 ) Resolvemos: Se realizan las operaciones que hay dentro de los paréntesis: A = 2 + (– 1) + 1 – (– 6) Y finalmente se opera ya sin paréntesis: A = 2 - 1 + 1 + 6 = 9 – 1 = 8 Sumas y diferencias CON PARÉNTESIS

13. Otro ejemplo: Sea la expresión: B = - 5 + (– 3 + 4 ) + 2 – ( - 7 + 6 – 8 ) Resolvemos: Se realizan las operaciones que hay dentro de los paréntesis: A = - 5 + (1) + 2 – (– 9) Y finalmente se opera ya sin paréntesis: A = - 5 + 1 + 2 + 9 = 12 – 5 = 7

14. Para hallar el producto de dos números enteros: 1.- Se multiplican sus valores absolutos. 2.- El resultado es un número positivo si los dos números tienen el mismo signo. 3.- El resultado es un número negativo si los dos números tienen el signo diferente. Regla de los signos de la multiplicación: (+) x (+) = (+) (+) x (-) = (-) (-) x (+) = (-) (-) x (-) = (+) Ejemplos: 4 x (-9) = - 36 ; (-3) x (- 7) = 21 MULTIPLICACIÓN DE NÚMEROS ENTEROS

15. En una división exacta se cumple siempre: Dividendo = divisor x cociente Dividir dos números entre sí es encontrar un tercer número cuyo producto por el divisor nos de el dividendo. Regla de los signos de la multiplicación: (+) : (+) = (+) (+) : (-) = (-) (-) : (+) = (-) (-) : (-) = (+) Ejemplos: 36 : (-9) = - 4 ; (-21) : (- 3) = 7 DIVISIÓN DE NÚMEROS ENTEROS

16. DIVISIÓN EXACTA: D =d.c Si un número (D=dividendo) se divide entre otro (d=divisor), se obtiene el cociente (c ). Si el resto es 0 entonces la división es exacta. DIVISIÓN ENTERA: D=d.c+r Si hay resto distinto de 0, entonces la división es entera.

17. EJEMPLO DE DIVISIÓN EXACTA: Dividendo = divisor x cociente 12 : 6 = 2  D =d.c  12 = 6.2 Pues D=12, d=6 y c=2 EJEMPLO DE DIVISIÓN ENTERA: Dividendo = divisor x cociente + resto 13 : 5 = 2 y de resto 3  D=d.c+r  13 = 5.2 + 3

18. SACAR FACTOR COMÚN Si tenemos 12 + 15 , a veces nos interesa sacar factor común. 12 = 3.4 15 = 3.5 El 12 y el 15 tienen un factor común, que es el 3. Lo extraemos: 12 + 15 = 3 .4 + 3 .5 = 3 .(4+5) Vemos si es verdad: 12 + 15 = 3.(4+5) , 27 = 3.9 , 27 = 27 La operación de sacar factor común es la inversa de aplicar la propiedad distributiva.

19. JERARQUÍA EN LAS OPERACIONES Cuando hay mezcla de sumas, productos, paréntesis, etc… Primero se realizan los PARÉNTESIS, si les hay. Si hay paréntesis anidados ( uno dentro de otro) se opera de dentro hacia fuera. Segundo las POTENCIAS y RAÍCES, si las hay. Tercero los PRODUCTOS y DIVISIONES, si los hay. Cuarto las SUMAS y RESTAS, si las hay Si hay una igualdad en el orden o jerarquía en las operaciones, se opera de IZQUIERDA a DERECHA.

20. Ejemplo 1 5 + 4 – 7 – 2 + 6 = Todas son sumas o restas, presentan el mismo orden jeraquico. Operamos de izquierda a derecha: = 5 + 4 – 7 – 2 + 6 = = 9 – 7 – 2 + 6 = = 2 – 2 + 6 = = 0 + 6 = = 6

21. Ejemplo 2 8 : 4 . 7 : 2 : 7 = Todas son productos o divisiones, presentan el mismo orden jerárquico. Operamos de izquierda a derecha: = 8 : 4 . 7 : 2 : 7 = = 2. 7 : 2 : 7 = = 14 : 2 : 7 = = 7 : 7 = = 1

22. Ejemplo 3 5 + 4.3 – 7.9 + 40:5 = Hay sumas, restas, productos y divisiones. Primero efectuamos los productos y divisiones de izquierda a derecha: = 5 + 4.3 – 7.9 + 40:5 = = 5 + 12 – 7.9 + 40:5 = = 5 + 12 – 63 + 40:5 = = 5 + 12 – 63 + 8 = Y después las sumas y restas de izquierda a derecha: = 5 + 12 – 63 + 8 = = 17 – 63 + 8 = = – 46 + 8 = = - 38

23. Ejemplo 4 : 5 + 4. (3 – 7) .9 + 40:5 = Vemos que hay un paréntesis. Será lo primero que efectuemos: = 5 + 4.(-4). 9 + 40:5 = Luego productos y divisiones, de izquierda a derecha: = 5 + (-16).9 + 40:5 = = 5 + (-144) + 40:5 = = 5 + (-144) + 8 = Y después las sumas y restas de izquierda a derecha: = 5 - 144 + 8 = = – 139 + 8 = = - 131

24. Ejemplo 5 : 5 + 4.[3 – 7.(9 – 2)] : 4. 5 + 2 = Vemos que hay un paréntesis anidado. 5 + 4.[3 – 7 .(9 – 2) ] : 4. 5 + 2 = Queda: 5 + 4 . [3 – 7.7] : 4. 5 + 2 = En el paréntesis que queda hay restas y productos. Queda: 5 + 4 . [3 – 49] : 4. 5 + 2 = 5 + 4 .[ – 46] : 4. 5 + 2 = Vemos que hay sumas, productos y divisiones. 

25.  5 + 4.[ – 46] : 4. 5 + 2 = Vemos que hay sumas, productos y divisiones. Productos y divisiones de izquierdas a derecha, quedando: 5 + [ – 184] : 4 . 5 + 2 = 5 + [ – 46] . 5 + 2 = Finalmente las sumas y restas de de izquierdas a derecha, quedando: 5 + [ – 230] + 2 = - 225 + 2 = - 223