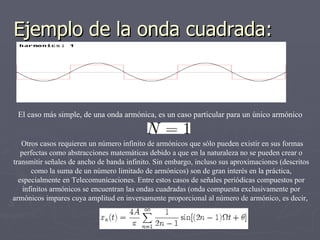
Este documento describe las ondas periódicas, las cuales muestran periodicidad respecto al tiempo y describen ciclos repetitivos. Las ondas periódicas más simples son las ondas sinusoidales, las cuales están completamente caracterizadas por su amplitud, frecuencia y fase. Sin embargo, las ondas más complejas pueden descomponerse en la suma de ondas sinusoidales a través de la serie de Fourier.

1. ONDAS PERIODICAS

2. Definición:
La mayoría de las ondas son el
resultado de muchas
perturbaciones sucesivas del
medio, y no sólo una. Cuando
dichas perturbaciones se
producen a intervalos regulares y
son todas de la misma forma,
estamos en presencia de una
onda periódica, y el número de
perturbaciones por segundo se
denomina frecuencia de la onda.

3. Estructura de la onda
PERIODO: FRECUENCIA:
Mínimo intervalo de tiempo Indica el número de veces
invertido por un fenómeno que se repite en un
periódico para volver a pasar segundo cualquier
por la misma posición. Se fenómeno periódico. Se
representa por T y se expresa mide en Hertz (Hz).
en segundos.

4. Las ondas periódicas son aquellas ondas que muestran periodicidad respecto
del tiempo, es decir, describen ciclos repetitivos.
En una onda periódica se cumple:
donde el periodo propio fundamental esta dado por:
siendo F, la frecuencia de la componente
fundamental de la onda periódica y n un número
entero.

5. La onda sinusoidal:
Toda onda periódica es, por definición, una onda determinista, por cuanto
puede ser descrita matemáticamente (mediante un modelo matemático).
La forma más simple de onda periódica es la onda armónica (sinusoidal),
que se describe matemáticamente como:
Esta onda está completamente caracterizada por tres parámetros: es la amplitud de la
sinusoide, es la frecuencia en radianes por segundo (rad/s), y es la fase en radianes.
En lugar de , a menudo se utiliza la frecuencia ciclos por segundo o hercios (Hz),
donde

6. Series de Fourier:
El modelo descrito para las ondas
armónicas no sirve para describir
estructuras periódicas más complicadas:
las ondas anarmónicas. Joseph Fourier
demostró que las ondas periódicas con
formas complicadas pueden considerarse
como suma de ondas armónicas (cuyas
frecuencias son siempre múltiplos enteros
de la frecuencia fundamental). Así,
supongamos que representa el
desplazamiento periódico de una onda en
una cierta posición. Si y su derivada
son continuas, puede demostrarse que
dicha función puede representarse
mediante una suma del tipo:

7. Otros principios de la serie:
El proceso de determinación matemática de los coeficientes y las constantes de fase
para una forma de onda dada se llama análisis de Fourier. Al igual que una forma de
onda periódica puede analizarse como una serie de Fourier mediante las contribuciones
relativas de la frecuencia fundamental y los armónicos superiores presentes en la forma de
onda, también es posible construir nuevas formas de onda periódicas, sumando a la
frecuencia fundamental distintas contribuciones de sus armónicos superiores. Este proceso
se denomina síntesis de Fourier.
Es importante notar que para las señales de ancho de banda limitado (en la práctica,
todas las de interés en Telecomunicaciones), la suma de armónicos es también finita:

8. Ejemplo de la onda cuadrada:
El caso más simple, de una onda armónica, es un caso particular para un único armónico
Otros casos requieren un número infinito de armónicos que sólo pueden existir en sus formas
perfectas como abstracciones matemáticas debido a que en la naturaleza no se pueden crear o
transmitir señales de ancho de banda infinito. Sin embargo, incluso sus aproximaciones (descritos
como la suma de un número limitado de armónicos) son de gran interés en la práctica,
especialmente en Telecomunicaciones. Entre estos casos de señales periódicas compuestos por
infinitos armónicos se encuentran las ondas cuadradas (onda compuesta exclusivamente por
armónicos impares cuya amplitud en inversamente proporcional al número de armónico, es decir,