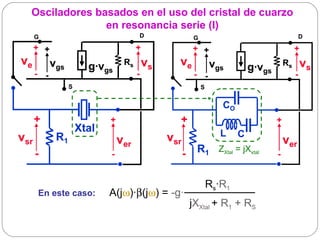
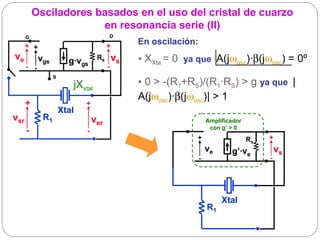
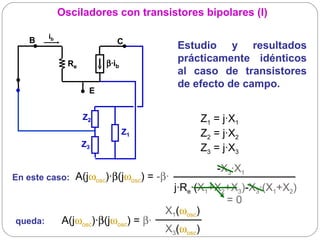
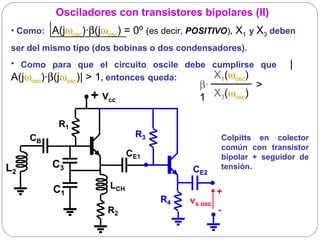
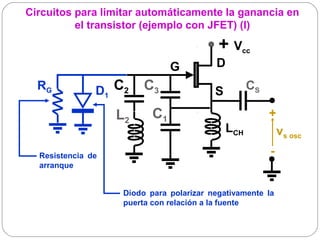
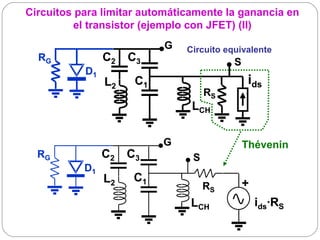
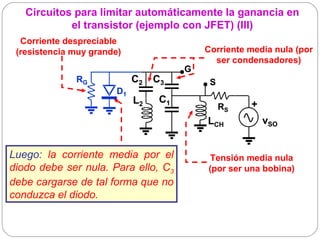
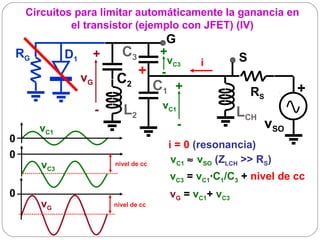
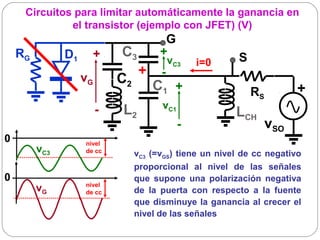
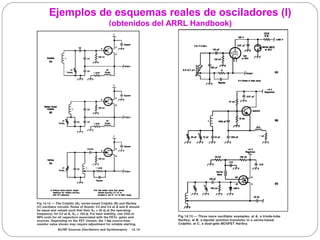
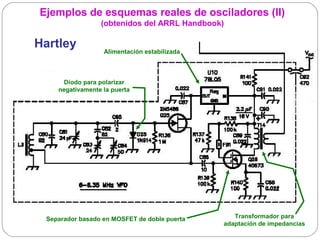
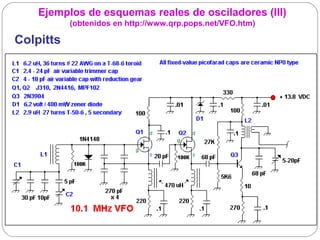
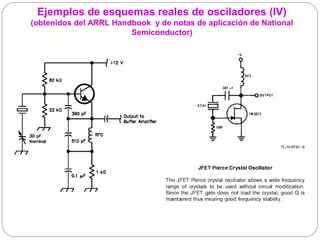
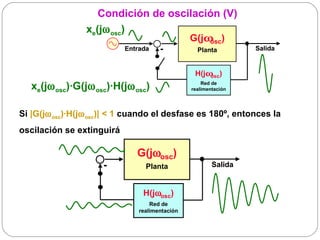
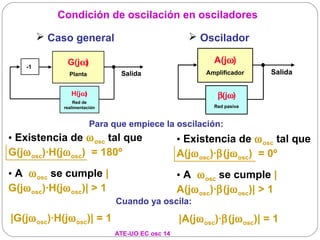
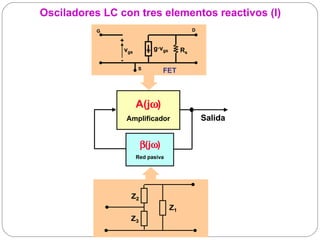
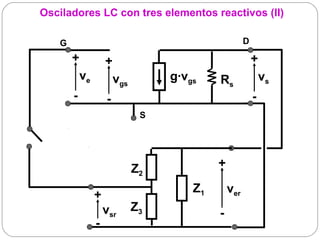
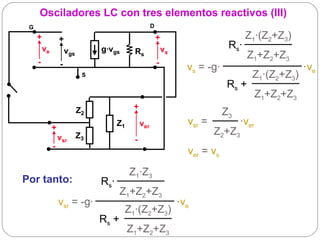
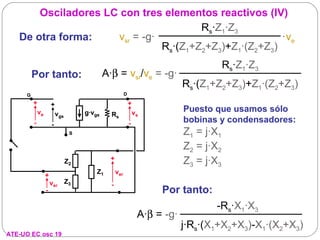
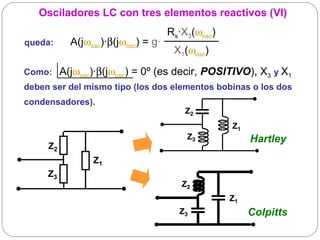
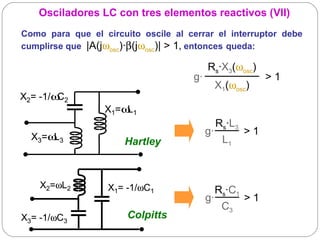
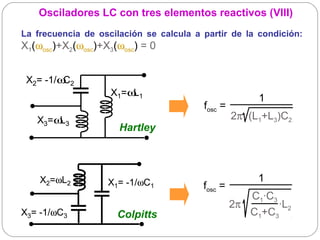
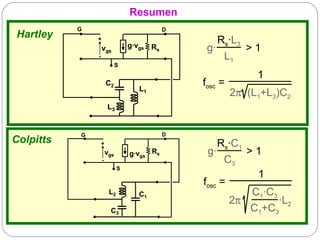
El documento resume los principios básicos de los osciladores electrónicos. Explica que un oscilador requiere realimentación positiva para generar una señal sinusoidal continua. Analiza los requisitos para que un circuito oscile, incluyendo que la ganancia en bucle cerrado debe ser mayor que 1 cuando la fase es de 180 grados. También describe los diferentes tipos de osciladores LC de tres elementos reactivos y sus condiciones para oscilar.

1. Circuitos electrónicos de Comunicaciones
CONTENIDO RESUMIDO:
1- Introducción
2- Osciladores
3- Mezcladores.
4- Lazos enganchados en fase (PLL).
5- Amplificadores de pequeña señal para RF.
6- Filtros pasa-banda basados en resonadores piezoeléctricos.
7- Amplificadores de potencia para RF.
8- Demoduladores de amplitud (AM, DSB, SSB y ASK).
9- Demoduladores de ángulo (FM, FSK y PM).
10- Moduladores de amplitud (AM, DSB, SSB y ASK).
11- Moduladores de ángulo (PM, FM, FSK y PSK).
12- Tipos y estructuras de receptores de RF.
13- Tipos y estructuras de transmisores de RF.
14- Transceptores para radiocomunicaciones

2. 2. Osciladores
Osciladores con elementos discretos
• de Baja Frecuencia (RC)
• de Alta Frecuencia y • Colpitts
Tipos de Frecuencia Variable (LC) • Hartley
Osciladores • Otros (Clapp, ...)
• de Alta Frecuencia y • Colpitts
Frecuencia Fija (a cristal) • Hartley
• Pierce
• Otros (Clapp, ...)

3. Teoría básica de sistemas realimentados
• Se linealiza el sistema
• Se toman transformadas de Laplace
xe(s) xer(s) G(s) xs(s)
Entrada - Planta Salida
xr(s) H(s)
Observaciones: Red de
xe: magnitud de entrada realimentación
xer: magnitud de error
xr: magnitud realimentada
xs: señal de salida
xx: magnitudes que pueden ser de distinto tipo
G(s): función de transferencia de la planta
H(s): función de transferencia de la red de realimentación

4. Cálculo de funciones de transferencia
xe(s) xer(s) G(s) xs(s)
Entrada - Planta Salida
xr(s) H(s)
Red de
realimentación
Lazo abierto Lazo cerrado
xs(s) xs(s) G(s)
G(s) = =
xer(s) xe(s) 1 + G(s)·H(s)

5. Casos particulares
xe(s) G(s) xs(s) xs(s) G(s)
Entrada - Planta Salida =
xe(s) 1 + G(s)·H(s)
H(s)
Red de
realimentación
Realimentación negativa  1 + G(s)·H(s) > 1
Alta ganancia de lazo xs(s)/xe(s) = 1/H(s)
Realimentación positiva  1 + G(s)·H(s) < 1
Oscilación  1 + G(s)·H(s) = 0
Situación indeseada en servosistemas
Situación deseada en osciladores

6. Caso de oscilación
xe(s) xs(s)
xs(s) G(s) G(s)
= Entrada - Planta Salida
xe(s) 1 + G(s)·H(s)
H(s)
Red de
realimentación
 1 + G(s)· H(s) = 0 xs(s)/xe(s) → ∞
Se genera Xs aunque no haya Xe Cuando está oscilando:
 G(s)· H(s) = 1
G(s)· H(s) = 180º
G(s) xs(s)
-1 Por tanto:
Planta Salida
 G(jω osc)· H(jω osc) = 1
H(s) G(jω osc)· H(jω osc) = 180º
Red de
realimentación

7. Condición de oscilación (I)
En oscilación: G(jω )
-1 osc
 G(jω osc)· H(jω osc) = 1 Planta Salida
G(jω osc)· H(jω osc) = 180º
H(jω )
osc
Red de
realimentación
¿Qué tiene que suceder para que comience la oscilación?
xe(jω osc)
G(jω )
osc
Entrada - Planta Salida
H(jω )
osc
Red de
realimentación
xe(jω osc)·G(jω osc)·H(jω osc)

8. Condición de oscilación (II)
xe(jω osc)
G(jω )
osc
Entrada - Planta Salida
H(jω )
osc
xe(jω osc)·G(jω osc)·H(jω osc) Red de
realimentación
Si |xe(jω osc)·G(jω osc)·H(jω osc)| > |xe(jω osc)| (es decir, |G(jω osc)·H(jω osc)| > 1)
cuando el desfase es 180º, entonces podemos hacer que la salida del
lazo de realimentación haga las funciones de la magnitud de entrada.
G(jωosc)
- Planta Salida
H(jωosc)
Red de
realimentación

9. Condición de oscilación (III)
En realidad si |G(jω osc)·H(jω osc)| > 1 cuando el desfase es 180º,
las magnitudes empezarán a crecer constantemente
G(jωosc)
- Planta Salida
H(jωosc)
Red de
realimentación
¿Existe un límite a este crecimiento?
Evidentemente sí, por razones energéticas hay límites. Incluso
el sistema podría destruirse al crecer la magnitud de salida.

10. Condición de oscilación (IV)
G(jωosc)
- Planta Salida
H(jωosc)
Red de
realimentación
|Gpm(jω osc)·H(jω osc)| > 1
|Ggm(jω osc)·H(jω osc)| = 1
Observaciones:
Gpm(s): función de transferencia de pequeña magnitud
Ggm(s): función de transferencia de gran magnitud

11. Condición de oscilación (V)
xe(jω osc)
G(jω )
osc
Entrada - Planta Salida
H(jω )
osc
xe(jω osc)·G(jω osc)·H(jω osc) Red de
realimentación
Si |G(jω osc)·H(jω osc)| < 1 cuando el desfase es 180º, entonces la
oscilación se extinguirá
G(jωosc)
- Planta Salida
H(jωosc)
Red de
realimentación

12. Condición de oscilación (VI)
Formulación formal: -1
G(jω )
osc
Criterio de Nyquist Planta Salida
H(jω )
osc
Red de
realimentación
 Para que empiece la oscilación:
• Tiene que existir una ω osc a la que se se cumpla
G(jω osc)·H(jω osc) = 180º
• A esa ω osc tiene que cumplirse |G(jω osc)·H(jω osc)| > 1
 Cuando se estabiliza la oscilación:
• Disminuye la G(jω osc) hasta que |G(jω osc)·H(jω osc)| = 1
cuando G(jω osc)·H(jω osc) = 180º

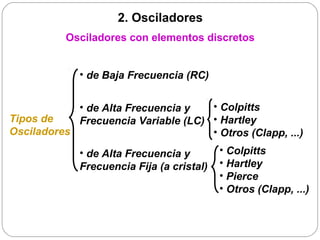
13. |G(jω)·H(jω)| [dB]
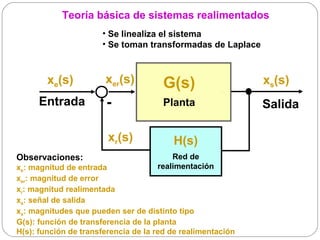
Condición de oscilación (VII) 80
Interpretación con 40
Oscilará
Diagramas de Bode 0
 Para que empiece la oscilación. -40
1 102 104 106
-1
G(jω )
osc
Planta Salida G(jω)·H(jω) [º]
H(jω ) 0
osc
Red de
realimentación -60
-120
-180
-240
1 102 104 106
ω osc
ATE-UO EC osc 12

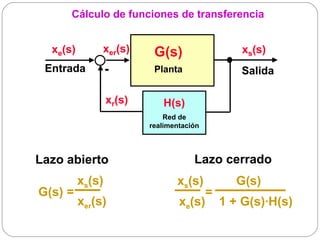
14. Condición de oscilación (VIII)
 Cuando ya oscila.  Para que no oscile.
|G(jω)·H(jω)| [dB] |G(jω)·H(jω)| [dB]
80 80
40 40
0 0
No
-40 -40 oscilará
G(jω)·H(jω) [º] G(jω)·H(jω) [º]
0 0
-60 -60
-120 -120
-180
ω osc -180
ω osc
-240 -240
1 102 104 106 ATE-UO EC osc 13 1 102 104 106

15. Condición de oscilación en osciladores
 Caso general  Oscilador
G(jω) A(jω)
-1
Planta Salida Amplificador Salida
H(jω) β(jω)
Red de
realimentación Red pasiva
Para que empiece la oscilación:
• Existencia de ω osc tal que • Existencia de ω osc tal que
G(jω osc)·H(jω osc) = 180º A(jω osc)·β(jω osc) = 0º
• A ω osc se cumple | • A ω osc se cumple |
G(jω osc)·H(jω osc)| > 1 A(jω osc)·β(jω osc)| > 1
Cuando ya oscila:
|G(jω osc)·H(jω osc)| = 1 |A(jω osc)·β(jω osc)| = 1
ATE-UO EC osc 14

16. Tipos de Osciladores
BJT, JFET, MOSFET, Amp. Integrados, etc
A(jω)
Amplificador Salida
β(jω)
Red pasiva
• RC en baja frecuencia.
• LC en alta frecuencia (y variable).
• Dispositivo piezoeléctrico en alta frecuencia (y constante).
• Líneas de transmisión en muy alta frecuencia.

17. Osciladores LC con tres elementos reactivos (I)
G D
+
vgs g·vgs Rs
-
S
FET
A(jω)
Amplificador Salida
β(jω)
Red pasiva
Z2
Z1
Z3

18. Osciladores LC con tres elementos reactivos (II)
G D
+ + +
ve vgs g·vgs Rs vs
- - -
S
Z2 +
Z1 ver
+
vsr Z3 -
-

19. Osciladores LC con tres elementos reactivos (III)
G D
+ + + Z1·(Z2+Z3)
ve vgs g·vgs vs Rs·
Rs
Z1+Z2+Z3
- - -
vs = -g· ·ve
S Z1·(Z2+Z3)
Rs +
Z1+Z2+Z3
+
Z2 Z3
Z1 ver vsr = ·ver
+
Z3 Z2+Z3
vsr -
-
ver = vs
Z1·Z3
Por tanto: Rs·
Z1+Z2+Z3
vsr = -g· ·ve
Z1·(Z2+Z3)
Rs +
Z1+Z2+Z3

20. Osciladores LC con tres elementos reactivos (IV)
Rs·Z1·Z3
De otra forma: vsr = -g· ·ve
Rs·(Z1+Z2+Z3)+Z1·(Z2+Z3)
Rs·Z1·Z3
Por tanto: A·β = vsr/ve = -g·
Rs·(Z1+Z2+Z3)+Z1·(Z2+Z3)
D
G
+ +
+
ve g·vgs vs Puesto que usamos sólo
vgs Rs
- - - bobinas y condensadores:
S Z1 = j·X1
Z2 = j·X2
Z2 +
Z3 = j·X3
Z1 ver
+
vsr Z3 -
- Por tanto:
-Rs·X1·X3
A·β = -g·
2+X3)-X1·(X2+X3)
j·Rs·(X1+X
ATE-UO EC osc 19

21. Osciladores LC con tres elementos reactivos (V)
Si el circuito debe oscilar al cerrar el interruptor, debe cumplirse que:
• Existe ωosc tal que A(jωosc)·β(jωosc) = 0º (es decir, REAL)
• A ωosc se cumple |A(jωosc)·β(jωosc)| > 1
-Rs·X1·X3
Por tanto: A(jωosc)·β(jωosc) = -g·
j·Rs·(X1+X2+X3)-X1·(X2+X3)
= 0
Como: X1(ωosc)+X2(ωosc)+X3(ωosc) = 0, los tres elementos
reactivos no pueden ser iguales. Tiene que haber dos bobinas y un
condensador o dos condensadores y una bobina.
Rs·X3(ωosc)
Queda: A(jωosc)·β(jωosc) = -g·
X2(ωosc)+X3(ωosc)
Y como: X2(ωosc)+X3(ωosc) = -X1(ωosc),

22. Osciladores LC con tres elementos reactivos (VI)
Rs·X3(ωosc)
queda: A(jωosc)·β(jωosc) = g·
X (ω )
1 osc
Como: A(jωosc)·β(jωosc) = 0º (es decir, POSITIVO), X3 y X1
deben ser del mismo tipo (los dos elementos bobinas o los dos
condensadores).
Z2
Z1
Z3 Hartley
Z2
Z1
Z3
Z2
Z1
Z3 Colpitts

23. Osciladores LC con tres elementos reactivos (VII)
Como para que el circuito oscile al cerrar el interruptor debe
cumplirse que |A(jωosc)·β(jωosc)| > 1, entonces queda:
Rs·X3(ωosc)
g· > 1
X1(ωosc)
X2= -1/ω 2
C
X1=ω 1
L
Rs·L3
g· > 1
X3=ω 3
L Hartley L1
X2=ωL2 X1= -1/ωC1 Rs·C1
g· > 1
C3
X3= -1/ωC3 Colpitts

24. Osciladores LC con tres elementos reactivos (VIII)
La frecuencia de oscilación se calcula a partir de la condición:
X1(ωosc)+X2(ωosc)+X3(ωosc) = 0
X2= -1/ω 2
C
X1=ω 1
L
1
fosc =
X3=ω 3
L 2π (L1+L3)C2
Hartley
X2=ωL2 X1= -1/ωC1 1
fosc =
C1·C3
2π ·L2
X3= -1/ωC3 Colpitts C1+C3

25. Resumen
G D
Hartley +
g·vgs
Rs·L3
vgs Rs g· > 1
- L1
S
1
C2 fosc =
L1
2π (L1+L3)C2
L3
G D
Colpitts + Rs·C1
vgs g·vgs Rs g· > 1
- C3
S
1
fosc =
L2 C1 C1·C3
2π ·L2
C3 C1+C3

26. Realización práctica de un Colpitts en “fuente común”
G D
G D +
+ +
vs osc
vgs g·vgs Rs vs osc S
- - * -
S
L2 C1
L2 C1
C3
C3
+ Vcc + Vcc
LCH LCH
CD
G D
D +
G CG D
G vs osc
L2
S S
*
S -
CS
CS
C1
C3

27. Realización práctica de un Colpitts en “puerta común”
G D G D +
+ + vs osc
S
-
vgs g·vgs Rs
-
vs osc
* -
S
L2 C1
L2 C1
C3
C3
+ Vcc
+ Vcc
L2
LCH CD
G D D G
D +
G vs osc
S C1
S -
S
* C3

28. Realización práctica de un Colpitts en “drenador común”
G D
G D
+
vgs g·vgs Rs S
- *
S
L2 C1 +
L2 C1 +
vs osc
C3 -
vs osc
C3 -
+ Vcc
+ Vcc G D
G D
S CS
D S L2 C3
G +
C1 LCH vs osc
S
*
LCH
-

29. Realización práctica de un Hartley en “fuente común”
G D
+ +
vgs g·vgs Rs vs osc
- -
S
+ Vcc
C2
L1 L1
L3 CD
C2 +
D
G
+ Vcc vs osc
LCH L3 S -
CS
D
G
S
CS

30. Realización práctica de un Hartley en “puerta común”
G D
+
g·vgs Rs
+
+ Vcc
vgs vs osc
- -
LCH
S
CD1
C2 +
L1 D vs osc
G CD2 -
L3 S
+ Vcc L1 C
2
L3
LCH
CM
D
G
S

31. Realización práctica de un Hartley en “drenador común”
G D
+
vgs g·vgs Rs
-
S
+ Vcc
CG G D
C2 C2 CS
L1 + S
vs osc L3 +
L3 - vs osc
-
L1
+ Vcc CM
G D
S
LCH

32. Osciladores LC con más de tres elementos reactivos:
El oscilador de Clapp (I)
G D
Condiciones de oscilación:
+
vgs g·vgs Rs·C1
Rs g· > 1
- C3
S 1
fosc =
C2 C1·C2·C3
2π ·L2
C1·C2+C1·C3+C2·C3
L2
C1
• C2 no influye en la condición |
C3
A(jωosc)·β(jωosc)| > 1
• C2 influye en la frecuencia de
oscilación, especialmente si C2 << C1,C3
• Especialmente útil para osciladores de frecuencia variable.

33. Osciladores LC con más de tres elementos reactivos:
El oscilador de Clapp (II)
Realización práctica en “drenador común”
+ Vcc
G D
RG S CS
L2 C3
+
C1 LCH vs osc
C2
-
R1

34. Osciladores de frecuencia variable (I)
Hay que hacer variar uno de los elementos reactivos de la red de
realimentación.
Tipos:
• Con control manual
• Controlado por tensión (Voltage Cotrolled Oscillator, VCO)
Con control manual de la frecuencia
Usando un condensador variable

35. Osciladores de frecuencia variable (II)
+ Vcc + Vcc
G D G D
RG S CS CS
S
L2 C3 C2 C3
+ L2
+
C1 LCH vs osc LCH
C1 vs osc
C2
- -
R1 R1
Clapp (Colpitts sintonizado en serie) Colpitts sintonizado en paralelo
en “drenador común” en “drenador común”
Rs·C1
Condiciones de oscilación: g· > 1 (común)
C3
1 1
fosc = fosc =
C1·C2·C3 C1·C3
2π ·L2 2π ( +C2)·L2
C1·C2+C1·C3+C2·C3 C1+C3

36. Osciladores de frecuencia variable (III)
Osciladores Controlado por Tensión (VCOs)
Se basan en el uso de diodos varicap (también llamados “varactores”)
+ Vcc
G D
RG S CS
L2 C3
+
RCF LCH vs osc
C1
C21 -
+ R1
vCF C22
-
C2

37. Hojas de características de un diodo varicap (BB131) (I)

38. Hojas de características de un diodo varicap (BB131) (II)

39. Osciladores de frecuencia muy constante
• Se basan en el uso de cristales de cuarzo (u otro
material piezoeléctrico)
• Símbolo:
• Interior del dispositivo:
Cristal
Contacto
metálico Cápsula
• Aspecto:
Terminales

40. Cristales piezoeléctricos (I)
• Circuito equivalente de un cristal de cuarzo:
R1 R2 R3
L1 L2 L3
C1 C2 C3
CO

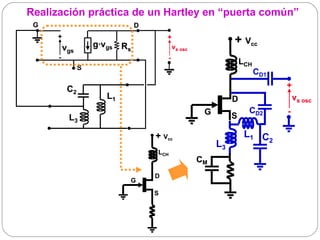
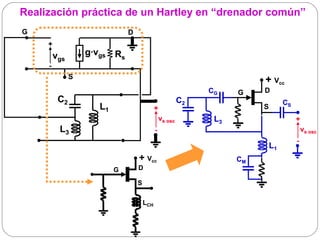
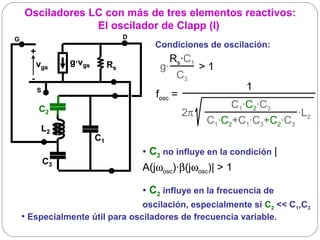
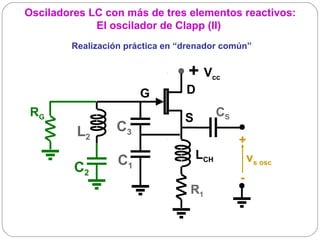
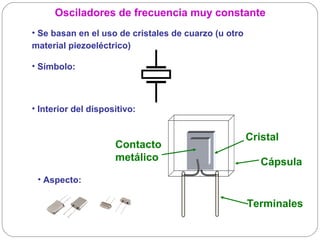
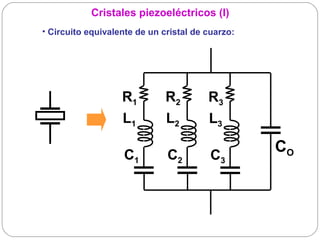
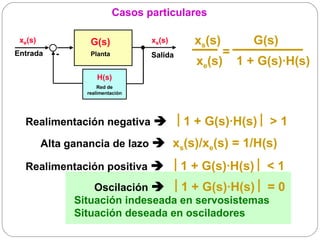
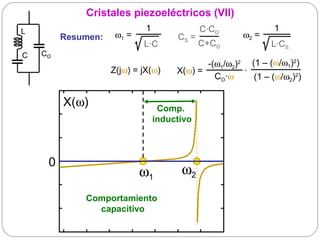
41. Cristales piezoeléctricos (II)
R1 R2 R3 Z(f)
L1 L2 L3
C1 C2 C3
CO
Im(Z(f)) [kΩ]
50
Comportamiento
inductivo
0
Comportamiento
-50 capacitivo
f1 f2

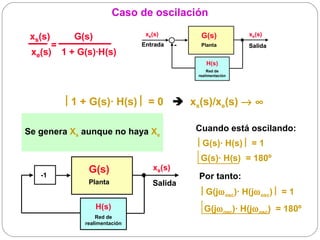
42. Cristales piezoeléctricos (III)
Modelo simplificado (alrededor de una de las frecuencias
en las que se produce comportamiento inductivo)
Ejemplo: cristal de µP de 10
MHz
R R = 20 Ω L = 15 mH
L C = 0,017 pF CO = 3,5 pF
CO
XL(10 MHz)= 2π·107·15·10-3 = 942 kΩ
C
Z(f)
Im(Z) [MΩ]
1
0
200 Hz
-1
10,0236 10,024 10,0244
f [MHz]

43. Cristales piezoeléctricos (IV)
Ejemplo: cristal de µP de 10 MHz
En otra escala
R = 20 Ω L = 15 mH C = 0,017 pF CO = 3,5 pF
Im(Z) [kΩ]
600
Margen de R
comportamiento inductivo
L
≈25 kHz CO
C
0
-600
10 10,01 10,02 10,03
f [MHz]

44. Cristales piezoeléctricos (V)
Calculamos la impedancia del modelo del cristal
L 1 1
(L·s + )
CO·s C·s 1 (L·C·s2 + 1)
Z(s) = = ·
1 1 CP·s (L·CS·s2 + 1)
C CO + L·s +
CO·s C·s
C·CO
siendo: CS = CP = C+CO
C+CO
Análisis senoidal: s = jω
-j (1 - L·C·ω2 ) -j(ω1/ω2)2 (1 – (ω/ω1)2)
Z(jω) = ·
= ·
CP·ω (1 - L·CS·ω2) CO·ω (1 – (ω/ω2)2)
1 1
siendo: ω1 = ω2 =
L·C L·CS

45. Cristales piezoeléctricos (VI)
L
-j(ω1/ω2)2 (1 – (ω/ω1)2) 1 1
Z(jω) = · ω1 = ω2 =
CO CO·ω (1 – (ω/ω2)2) L·C L·CS
C
Como CS < C, entonces: ω 2 > ω 1
• Si ω < ω 1, entonces también ω < ω 2 y entonces:
Z(jω) = -j·(cantidad positiva) < 0, es decir, comportamiento capacitivo.
• Si ω 1 < ω < ω 2, entonces:
Z(jω) = -j·(cantidad negativa) > 0, es decir, comportamiento inductivo.
• Si ω 2 < ω, entonces también ω 1 < ω y entonces:
Z(jω) = -j·(cantidad positiva) < 0, es decir, comportamiento capacitivo.
Solo se comporta de modo inductivo si ω 1 < ω < ω 2

46. Cristales piezoeléctricos (VII)
L 1 C·CO 1
Resumen: ω1 = CS = ω2 =
L·C C+CO L·CS
C CO
-(ω1/ω2)2 (1 – (ω/ω1)2)
Z(jω) = jX(ω) X(ω) = ·
CO·ω (1 – (ω/ω2)2)
X(ω) Comp.
inductivo
0
ω1 ω2
Comportamiento
capacitivo

47. Hojas de características de cristales de cuarzo

48. Osciladores a cristal
Se basan en el uso de una red de realimentación que incluye un
dispositivo piezoeléctrico (típicamente un cristal de cuarzo).
Tipos:
• Basados en la sustitución de una bobina por un cristal de cuarzo
en un oscilador clásico (Colpitts, Clapp, Hartley, etc.) ⇒ El cristal
de cuarzo trabaja el su zona inductiva.
• Basados en el uso del cristal de cuarzo en resonancia serie.
Basados en la sustitución de una bobina por un cristal (I)
+ Vcc + Vcc
G D D
G
RG S CS RG CS
C3 S
L2 C3
+ +
Xtal
C1 LCH vs osc LCH vs osc
C1
C2
- -
R1 R1

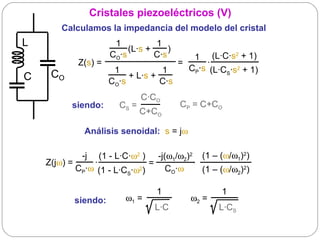
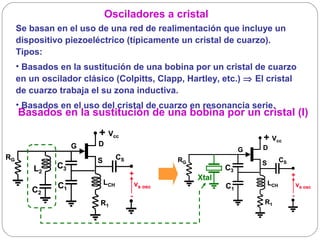
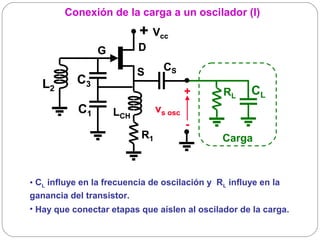
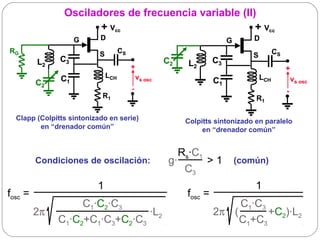
49. Osciladores basados en la sustitución de una bobina
por un cristal (II)
+ Vcc Condiciones de oscilación:
G D
CS
Rs·C1
RG
C3
S g· > 1 (no depende del cristal)
+
C3
Xtal
C1 LCH vs osc Cálculo de la frecuencia de oscilación :
-
R1 XC1(ωosc)+XC3(ωosc)+XXtal(ωosc) = 0
Cristal de 10 MHz
Gráficamente:
L = 15 mH R = 20 Ω
C = 0,017 pF CO = 3,5 pF 1000
-(XC1(ω)+XC3(ω)), XXtal(ω)
XXtal(ω)
C1 = C3 = 50pF
500
C1 = C3 = 100pF
[Ω]
C1 = C3 = 500pF
0
f [MHz]
10 10,002 10,004

50. Osciladores basados en la sustitución de una bobina
por un cristal (III)
Analíticamente:
XC1(ωosc)+XC3(ωosc)+XXtal(ωosc) = 0
-(ω1/ω2)2 (1 – (ωosc /ω1)2)
XXtal(ωosc) = ·
CO·ωosc (1 – (ωosc /ω2)2)
-1 -1
XC1(ωosc) + XC3(ωosc) = +
C1·ωosc C3·ωosc
Despejando ωosc se obtiene:
C
ωosc = ω1 1 +
C1·C3
+ CO
C1+C3
Nótese que ω 1 < ωosc < ω 2 ya que:
C
ω2 = ω1 1 +
CO

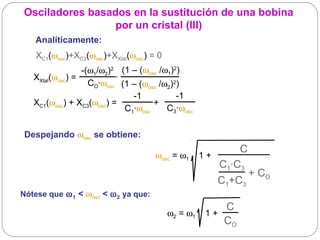
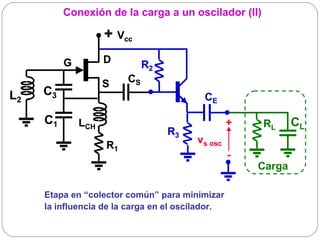
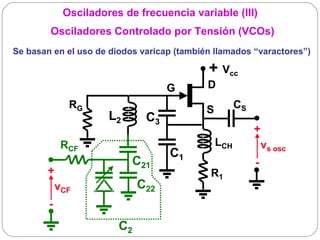
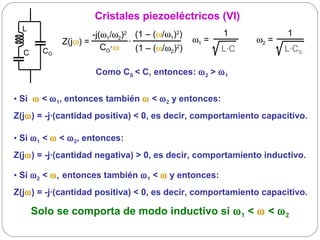
51. Osciladores basados en la sustitución de una bobina
por un cristal (IV)
Ajuste de la frecuencia de oscilación: modificar el valor de C O
externamente poniendo un condensador Cext en paralelo con el cristal
+ Vcc
C G D
ωosc = ω1 1 + CS
RG
C1·C3 C3
S
+ CO + Cext Cext Xtal +
C1+C3 C1 LCH vs osc
10 MHz -
R1
XXtal, -(XC1 + XC3) [Ω]
1500
Cext = 15pF 10pF
1000
-(XC1 + XC3) 5pF fosc(Cext= 0pF) = 10.002,9622 kHz
500 C1 = C3 = 50pF xXtal fosc(Cext= 5pF) = 10.002,5201 kHz
0pF fosc(Cext= 10pF) = 10.002,1929 kHz
0 fosc(Cext= 15pF) = 10.001,9408 kHz
9,999 10 10,001 10,002 10,003
f [MHz]

52. Osciladores basados en el uso del cristal de cuarzo
en resonancia serie (I)
G D G D
+ + + + + +
ve vgs g·vgs Rs vs ve vgs g·vgs Rs vs
- - - - - -
S S
CO
+ + + +
Xtal L C
vsr R1 ver vsr ver
- - - R1 ZXtal = jXxtal -
Rs·R1
En este caso: A(jω)·β(jω) = -g·
+ R1 + RS
jXXtal

53. Osciladores basados en el uso del cristal de cuarzo
en resonancia serie (II)
G D
+ + +
En oscilación:
ve vgs g·vgs Rs vs • XXta = 0 ya que A(jωosc)·β(jωosc) = 0º
- - -
S
jXxtal • 0 > -(R1+RS)/(R1·RS) > g ya que |
A(jωosc)·β(jωosc)| > 1
+ +
Xtal
vsr R1 ver Amplificador
con g’ > 0
- -
+ Rs +
ve g’·ve vs
- -
Xtal
R1

54. Conexión de la carga a un oscilador (I)
+ Vcc
G D
S CS
L2 C3
+ RL CL
C1 LCH vs osc
-
R1 Carga
• CL influye en la frecuencia de oscilación y RL influye en la
ganancia del transistor.
• Hay que conectar etapas que aíslen al oscilador de la carga.

55. Conexión de la carga a un oscilador (II)
+ Vcc
G D R2
S CS
L2 C3 CE
C1 LCH + RL CL
R3
vs osc
R1
-
Carga
Etapa en “colector común” para minimizar
la influencia de la carga en el oscilador.

56. Osciladores con transistores bipolares (I)
ib
B C
Estudio y resultados
Re β·ib
prácticamente idénticos
al caso de transistores
de efecto de campo.
E
Z2 Z1 = j·X1
Z1 Z2 = j·X2
Z3
Z3 = j·X3
-X3·X1
En este caso: A(jωosc)·β(jωosc) = -β·
j·Re·(X1+X2+X3)-X3·(X1+X2)
= 0
X1(ωosc)
queda: A(jωosc)·β(jωosc) = β·
X3(ωosc)

57. Osciladores con transistores bipolares (II)
• Como: A(jωosc)·β(jωosc) = 0º (es decir, POSITIVO), X1 y X3 deben
ser del mismo tipo (dos bobinas o dos condensadores).
• Como para que el circuito oscile debe cumplirse que |
A(jωosc)·β(jωosc)| > 1, entonces queda: X1(ωosc)
β· >
+ Vcc 1 X3(ωosc)
R1
CB R3 Colpitts en colector
común con transistor
CE1 bipolar + seguidor de
L2 C3 CE2 tensión.
C1 LCH
+
R4 vs osc
R2 -

58. Circuitos para limitar automáticamente la ganancia en
el transistor (ejemplo con JFET) (I)
+ Vcc
G D
RG D1 C2 C3 S CS
L2 C1 +
LCH vs osc
Resistencia de -
arranque
Diodo para polarizar negativamente la
puerta con relación a la fuente

59. Circuitos para limitar automáticamente la ganancia en
el transistor (ejemplo con JFET) (II)
G Circuito equivalente
RG C2 C3 S
D1
L2 C1 ids
RS
LCH
G Thévenin
RG C2 C3 S
D1
L2 C1 +
RS
LCH ids·RS

60. Circuitos para limitar automáticamente la ganancia en
el transistor (ejemplo con JFET) (III)
Corriente despreciable
(resistencia muy grande) Corriente media nula (por
ser condensadores)
G
RG C2 C3 S
D1
L2 C1 +
RS
LCH vSO
Luego: la corriente media por el Tensión media nula
diodo debe ser nula. Para ello, C3 (por ser una bobina)
debe cargarse de tal forma que no
conduzca el diodo.

61. Circuitos para limitar automáticamente la ganancia en
el transistor (ejemplo con JFET) (IV)
G
RG D1 + C3 + S
vC3 i
+ -
vG C2 C1 + RS +
vC1
- L2 LCH
vC1 - vSO
0
i = 0 (resonancia)
0 vC1 ≈ vSO (ZLCH >> RS)
vC3 nivel de cc
vC3 = vC1·C1/C3 + nivel de cc
0 vG = vC1+ vC3
vG nivel de cc

62. Circuitos para limitar automáticamente la ganancia en
el transistor (ejemplo con JFET) (V)
G
RG D1 + C3 + S
vC3 i=0
+ -
vG C2 C1 + RS +
vC1
- L2 LCH
- vSO
0 nivel
vC3 de cc
vC3 (=vGS) tiene un nivel de cc negativo
proporcional al nivel de las señales
0 que supone una polarización negativa
nivel
vG de cc de la puerta con respecto a la fuente
que disminuye la ganancia al crecer el
nivel de las señales

63. Condensadores adecuados para osciladores
de alta frecuencia
Deben ser condensadores cuya capacidad varíe muy poco
con la frecuencia. Ejemplos:
• Condensadores cerámicos NP0.
• Condensadores de aire (los variables)
• Condensadores de mica.
• Condensadores de plásticos de tipo Styroflex.
Cerámicos NP0 Styroflex.
Mica

64. Ejemplos de esquemas reales de osciladores (I)
(obtenidos del ARRL Handbook)

65. Ejemplos de esquemas reales de osciladores (II)
(obtenidos del ARRL Handbook)
Hartley
Alimentación estabilizada
Diodo para polarizar
negativamente la puerta
Separador basado en MOSFET de doble puerta Transformador para
adaptación de impedancias

66. Ejemplos de esquemas reales de osciladores (III)
(obtenidos en http://www.qrp.pops.net/VFO.htm)
Colpitts

67. Ejemplos de esquemas reales de osciladores (IV)
(obtenidos del ARRL Handbook y de notas de aplicación de National
Semiconductor)

68. Parámetros características de los osciladores
• Margen de frecuencia.
• Estabilidad ⇒ Mayor cuanto mayor es el factor de calidad “Q” de la
red de realimentación.
• Potencias (absoluta de salida sobre 50Ω ) y rendimientos
(Potencia de señal / potencia de alimentación).
• Nivel de armónicos y espurias ⇒ potencias relativas de uno o
varios armónicos con relación al fundamental.
• “Pulling” o estabilidad frente a la carga ⇒ uso de separadores.
• “Pushing” o estabilidad frente a la alimentación ⇒ uso de
estabilizadores de tensión (zeners, 78LXX, etc.).
•Deriva con la temperatura ⇒ Condensadores NP0, de mica, etc.
•Espectro de ruido ⇒ Se debe fundamentalmente a ruido de fase.