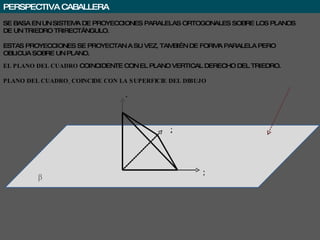
El documento describe diferentes sistemas de proyección y representación del espacio, incluyendo proyección paralela, central, oblicua y perspectiva caballera. Explica que la proyección paralela proyecta rayos paralelos desde el origen hacia el plano de proyección, mientras que la proyección central usa un punto de fuga finito. También define la perspectiva caballera como un sistema de proyecciones paralelas ortogonales sobre un triedro, proyectadas luego de forma oblicua sobre un plano de cuadro.

1. LA REPRESENTACIÓN DEL ESPACIO

2. LA REPRESENTACIÓN DEL ESPACIO

3. SISTEMAS DE PROYECCIÓN A B C A 1 B 1 C 1 PROYECCIÓN PARALELA O CILÍNDRICA: ORIGEN PUNTO INFINITO o PUNTO IMPROPIO β β A B C A 1 B 1 C 1 A B C A 1 B 1 C 1 PROYECCIÓN CENTRAL O CÓNICA: ORIGEN PUNTO FINITO o PUNTO PROPIO β V PROYECCIÓN PARALELA OBLICUA SISTEMAS DE REPRESENTACIÓN _PROYECCIÓN MEDIANTE RAYOS PROYECTANTES (LINEAS IMAGINARIAS) PROYECCIÓN PARALELA ORTOGONAL

4. SISTEMAS DE REPRESENTACIÓN A B C A 1 B 1 C 1 PROYECCIÓN PARALELA O CILÍNDRICA PROYECCIÓN PARALELA ORTOGONAL β 1. SISTEMA DIÉDRICO 2. SISTEMA DE PLANOS ACOTADOS 3. SISTEMA AXONOMÉTRICO

5. SISTEMAS DE REPRESENTACIÓN β A B C A 1 B 1 C 1 PROYECCIÓN PARALELA O CILÍNDRICA PROYECCIÓN PARALELA OBLICUA 1. SISTEMA DE PERSPECTIVA CABALLERA

6. SISTEMAS DE REPRESENTACIÓN A B C A 1 B 1 C 1 PROYECCIÓN CENTRAL O CÓNICA β 1. PERSPECTIVA CÓNICA V

7. REPRESENTACIÓN DEL ESPACIO 2D A 3D

8. REPRESENTACIÓN DEL ESPACIO 2D A 3D

9. REPRESENTACIÓN DEL ESPACIO 3D A 2D Y X Z Z Z Y X X X 0 0 0

10. PERSPECTIVA CABALLERA Y Z X β SE BASA EN UN SISTEMA DE PROYECCIONES PARALELAS ORTOGONALES SOBRE LOS PLANOS DE UN TRIEDRO TRIRECTÁNGULO. ESTAS PROYECCIONES SE PROYECTAN A SU VEZ, TAMBIÉN DE FORMA PARALELA PERO OBLICUA SOBRE UN PLANO. EL PLANO DEL CUADRO COINCIDENTE CON EL PLANO VERTICAL DERECHO DEL TRIEDRO. PLANO DEL CUADRO_COINCIDE CON LA SUPERFICIE DEL DIBUJO

11. PERSPECTIVA CABALLERA (Y) Z-(Z) X-(X) P γ α β Z X Y LOS EJES Y EL COEFICIENTE DE REDUCCIÓN 90º LOS EJES XZ SIEMPRE FORMAN 90º EL EJE Y DEPENDE DEL ANGULO DE INCLINACIÓN γ β γ α Y

12. PERSPECTIVA CABALLERA Z X Y LOS EJES Y EL COEFICIENTE DE REDUCCIÓN 90º α = 30º 45º 60º 120º 135º 150º X=z=1 ESTÁN CONTENIDOS EN EL PLANO Y DEPENDE DEL ÁNGULO DE INCLINACIÓN, VENDRÁ FIJADO POR CONDICIONES DE PROPORCIONALIDAD DE LA PERSPECTIVA SE LE APLICA UN COEFICIENTE DE REDUCCIÓN β α α = 30º 150º CR=0.6 α = 45º 135º CR=0.5 α = 60º 120º CR=0.8

13. PERSPECTIVA CABALLERA Z Z Y X y X 0 0 0 3 cm 4 cm 2 cm