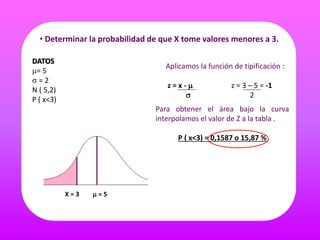
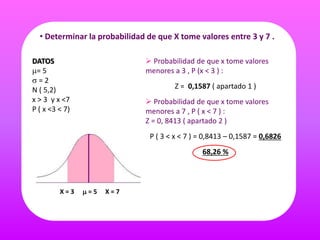
El documento describe cómo calcular diferentes probabilidades para una variable aleatoria X que sigue una distribución normal con parámetros μ=5 y σ=2. Se pide determinar la probabilidad de que X tome valores menores a 3, mayor a 7, y entre 3 y 7. También se pide determinar un intervalo centrado en la media tal que la probabilidad de que X pertenezca a ese intervalo sea 0.62.