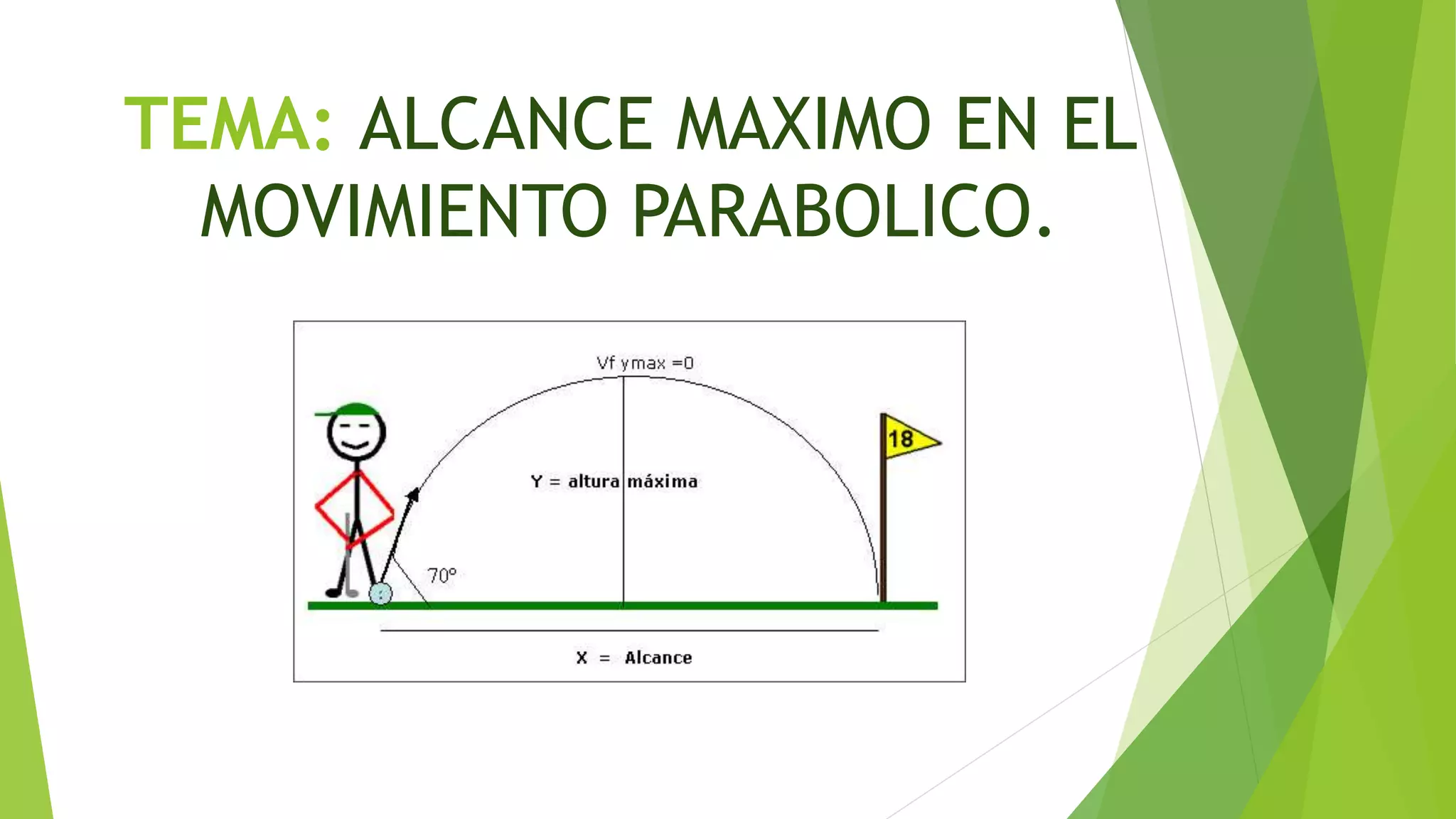
El documento explica la ecuación para calcular el alcance máximo horizontal de un proyectil en movimiento parabólico. La ecuación es Xmax=vo2sen(2α)/g, donde vo es la velocidad inicial, α es el ángulo de lanzamiento y g es la gravedad. El documento calcula el alcance máximo para diferentes ángulos de lanzamiento entre 20° y 90° para mostrar cómo varía el alcance con el ángulo.

1. TEMA: ALCANCE MAXIMO EN EL
MOVIMIENTO PARABOLICO.

3. ALCANCE MAXIMO HORIZONTAL
yf=yₒ+v₀Senαt-gt²/2
0=0+v₀Senαt-gt²/2
t=2vₒsenα/g
El tiempo que obtenemos es el tiempo que el proyectil estará en el aire
Reemplazo en la ecuación del alcance horizontal:(x=vₒ . Cos(α). t)
x=vₒ²sen.cos (2α)/g
Nota: 2Sen α Cos α =sen2 α
Xmax=vₒ²sen(2α)/g

4. ECUACION: Xmax=vₒ²sen(2α)/g
Sen(2 α)
 A UN ANGULO DE 70°
:Sen(2 α)
:Sen(2)(45)°
:1
 A UN ANGULO DE 20°
:Sen(2 α)
:Sen(2)(20)°
:0.64
 A UN ANGULO DE 70°
:Sen(2 α)
:Sen(2)(70)°
:0.64
 A UN ANGULO DE 90
:Sen(2 α)
:Sen(2)(90)°
:0

5. A UN ANGULO DE 45°
 DATOS:
Ɵ: 45°
Dx:0.7m
Vo: ?
Vo=
𝑑𝑥.𝑔
𝑆𝑒𝑛 2Ɵ
=
0.7𝑚.(
9.8𝑚
𝑠2 )
𝑆𝑒𝑛 2(𝟒𝟓°)
= 2.61 m/s
 Xmax=vₒ²sen(2α)/g
Xmax= (2.61)2
m/s . Sen(2)(45)/9.8m/𝑠2
Xmax=6.8m/s . 1/9.8m/𝑠2
Xmax=0.69m

6. CONCLUCION:
 A UN ANGULO DE 45°: 0.7m
 A UN ANGULO DE 20°: 0.63m
 A UN ANGULO DE 70 °: 0.26m
 A UN ANGULO DE 90°: 0m