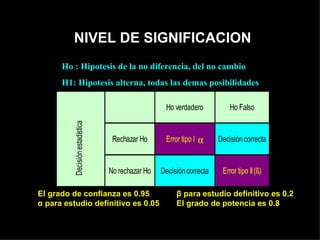
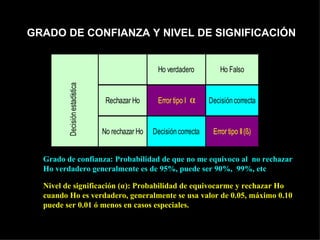
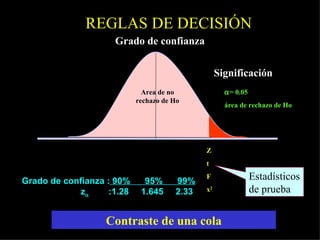
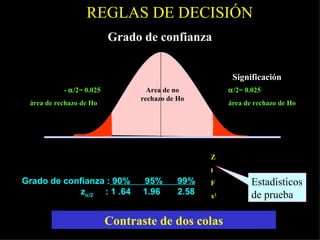
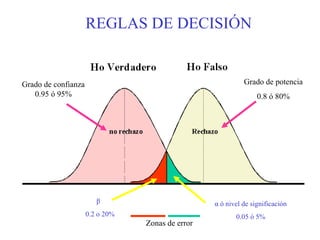
Este documento describe los pasos para realizar una prueba de hipótesis estadística, incluyendo plantear hipótesis nula y alternativa, establecer el nivel de significación, aplicar un estadístico de prueba, establecer una regla de decisión y sacar una conclusión. También explica conceptos como grado de confianza, nivel de significación, grado de potencia y zonas de error. Finalmente, detalla cómo realizar pruebas de hipótesis para medias, proporciones y comparaciones múltiples.

1. PRUEBA DE
HIPOTESIS
UNIVERSIDAD LA SALLE

2. DECISIONES ESTADÌSTICAS
En la practica con frecuencia tenemos que tomar
decisiones relativas a una población sobre la base
de la información proveniente de una muestra
Para ello es útil plantear hipótesis estadìsticas
(conjeturas) sobre la poblaciòn implicada y estas
pueden o no ser ciertas

3. Hipótesis estadística
Afirmación de lo que creemos sobre
una población. Por lo general se
refiere a los parámetros de la
población acerca de la cual se quiere
hacer la afirmación.

4. Prueba de hipótesis
Prueba, test o contraste de hipotesis es una
técnica estadística que se sigue para decidir
si rechazamos o no una hipótesis estadística
en base a la información de una muestra.
El propósito de la prueba o de hipótesis es
ayudar al investigador a tomar decisiones
referentes a una población considerando la
información de una muestra de dicha
población.

5. PASOS PARA LA PRUEBA DE HIPOTESIS
•Plantear las hipótesis
•Ho : μ1 - μ2 = 0
•H1 : μ1 - μ2 ≠ 0
•Establecer el nivel de significación α = 0.05
•Aplicar el estadístico de prueba, previo comprobación
de supuestos como la distribución de la población,
igualdad de varianzas, etc
•Establecer regla de decisión
•Sacar la conclusión

6. Plantear hipótesis
Para este fin se plantea:
Una hipótesis Nula (H0): Formulada con el unico
proposito de rechazarla o invalidarla, de la no
diferencia, del no cambio, de que no es bueno, de la
no asociaciòn (independencia), etc.
Una hipótesis alternativa (H1): Es la hipotesis que
difiere de la hipotesis nula, si H0 plantea =, H1
plantearà >, <, ò ≠

7. Contrastes de hipótesis
Planteadas H0 y H1 se procederá a contrastarlas pero
para ello debe fijarse las reglas de decisión
Suponiendo que una hipótesis particular es cierta
pero los resultados hallados en una muestra
aleatoria difieren notablemente de lo esperado
entonces diremos que las diferencias observadas son
significativas y nos veremos inclinados a rechazar la
hipótesis o al menos a no aceptarla pero cabe la
posibilidad de equivocarnos

8. NIVEL DE SIGNIFICACION
Ho : Hipotesis de la no diferencia, del no cambio
H1: Hipotesis alterna, todas las demas posibilidades
Ho verdadero Ho Falso
Decisión estadística
Rechazar Ho α
Error tipo I (a) Decisión correcta
No rechazar Ho Decisión correcta Error tipo II (ß)
El grado de confianza es 0.95 β para estudio definitivo es 0.2
α para estudio definitivo es 0.05 El grado de potencia es 0.8

9. GRADO DE CONFIANZA Y NIVEL DE SIGNIFICACIÓN
Decisión estadística Ho verdadero Ho Falso
Rechazar Ho α
Error tipo I (a) Decisión correcta
No rechazar Ho Decisión correcta Error tipo II (ß)
Grado de confianza: Probabilidad de que no me equivoco al no rechazar
Ho verdadero generalmente es de 95%, puede ser 90%, 99%, etc
Nivel de significación (α): Probabilidad de equivocarme y rechazar Ho
cuando Ho es verdadero, generalmente se usa valor de 0.05, máximo 0.10
puede ser 0.01 ó menos en casos especiales.

10. GRADO DE POTENCIAY β
Decisión estadística Ho verdadero Ho Falso
Rechazar Ho α
Error tipo I (a) Decisión correcta
No rechazar Ho Decisión correcta Error tipo II (ß)
Grado de potencia o valor predictivo: Probabilidad de que no me
equivoco al rechazar Ho falso generalmente es de 80%
β : Probabilidad de equivocarme al no al rechazar Ho que es falso
generalmente se usa valor de 0.2

11. REGLAS DE DECISIÓN
Grado de confianza
Significación
Area de no α= 0.05
rechazo de Ho
área de rechazo de Ho
Z
t
Grado de confianza : 90% 95% 99%
F Estadísticos
zα :1.28 1.645 2.33 x2 de prueba
Contraste de una cola

12. REGLAS DE DECISIÓN
Grado de confianza
Significación
- α/2= 0.025 Area de no α/2= 0.025
rechazo de Ho
área de rechazo de Ho área de rechazo de Ho
Z
t
Grado de confianza : 90% 95% 99% F Estadísticos
zα/2 : 1 .64 1.96 2.58 x2 de prueba
Contraste de dos colas

13. REGLAS DE DECISIÓN
Grado de confianza Grado de potencia
0.95 ó 95% 0.8 ó 80%
β α ó nivel de significación
0.2 o 20% 0.05 ó 5%
Zonas de error

14. PRUEBA DE HIPOTESIS PARA MEDIA DE
UNA SOLA POBLACION
Ho : μ1 = 30
H1 : μ1 ≠ 30
Supuesto distribución normal
varianza poblacional
conocida desconocida
x−µ x−µ
z= t=
σ S
n n
Puede darse Ho : μ1 ≥ 30 ó Ho : μ1 ≤ 30
SPSS: Analyze/compare means/ One sample t test (dos colas)

15. COMPARACIÓN DE DOS MEDIAS
INDEPENDIENTES
Ho : μ 1 - μ 2 = 0
H1 : μ1 - μ2 ≠ 0
En la práctica el valor de varianzas poblacionales se desconoce y
las varianzas muestrales siempre tienen pequeñas diferencias por
ello se saca la varianza mancomunada
2 2
( n − 1) S1 + (n2 − 1) S 2 Sm 2 Sm 2
Sm2 = 1 ESE1 -E 2 = +
n1 + n2 − 2 n1 n2
x1 − x 2 − ( µ1 − µ 2 )
t( n1 + n2 −2 ) =
ESX1 -X 2
SPSS: Analyze/compare means/ Independent sample t test

16. COMPARACIÓN DE DOS MEDIAS
RELACIONADAS
Ho : μ1 - μ2 = 0
H1 : μ1 - μ2 ≠ 0
En la práctica el valor de varianzas poblacionales se desconoce y
las varianzas muestrales siempre tienen pequeñas diferencias por
ello se saca la varianza mancomunada
Sd
∑ di =∑
2 (d i − d ) 2 ESd =
d= Sd
n −1 n
n
d − µ do d − µ do
Z= t=
σd Sd
n n
SPSS: Analyze/compare means/ Paired sample t test

17. PRUEBA DE HIPOTESIS PARA UNA
SOLA PROPORCION
Ho : p de aciertos igual a proporcion de desaciertos
H1 : p de aciertos diferente a proporcion de desaciertos
pq (p− p )
ESp = Z =
n ESp
Minitab: Stat / basic statistics / proportion

18. PRUEBA DE HIPOTESIS PARA
DIFERENCIA DE DOS PROPORCIONES
Ho : p 1 - p 2 = 0
H1 : p1 - p2 ≠ 0
se saca la proporción mancomunada
n1 p1 + n2 p 2 pm qm pm qm
Pm = ESp1 - p 2 = +
n1 + n2 n1 n2
p1 − p 2 − ( p1 − p2 )
Z =
ESp1 -p 2
Minitab: Stat / basic statistics /
proportions

19. COMPARACIÓN DE K MEDIAS
Ho : μ1 = μ2 = μ3 = μ4
H1 : Al menos dos medias son diferentes
Y  y.12 y.2 2 y.k  Y .....
2
SCT = ( y11 + y12 + ..... + yik ) − SCEG = 
 n + n + ..... + n  − N
N  
SCDG = SCT + SCEG
SCEG
CMEG =
K −1 CMEG
F( K −1, N − K ) =
SCDG CMDG
CMDG =
N −K
SPSS: Analyze/compare means/ one way ANOVA

20. Le agradeceremos nos haga llegar
sus observaciones y comentarios
Escribanos a freddy_g_o@yahoo.es