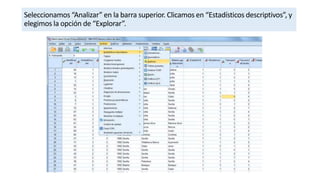
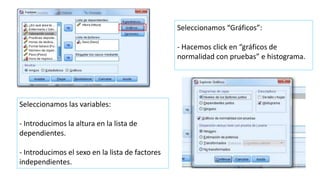
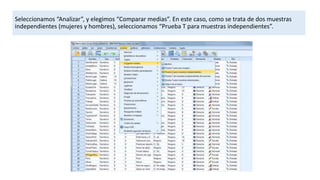
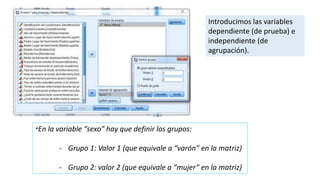
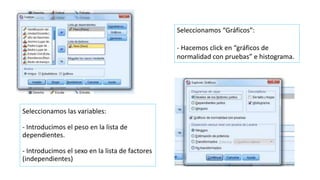
Este documento describe cómo realizar dos contrastes de hipótesis mediante la prueba T de Student en SPSS. El primer contraste examina la relación entre el sexo y la altura, mientras que el segundo analiza la relación entre el sexo y el peso. Ambos contrastes siguen los mismos pasos: comprobar la normalidad de las variables dependientes, seleccionar la prueba T para muestras independientes e interpretar los resultados.

1. SPSS: Test de T-STUDENT
Mª del Mar Torres Vilches
Grupo 1, subgrupo 5

2. Tarea del seminario 8
• Establecer dos contrastes de hipótesis mediante el test de T-Student
en SPSS.
• Utilizar en cada una de esas hipótesis dos variables de la matriz de
datos trabajada en clase:
 Una variable independiente cualitativa dicotómica.
 Una variable dependiente cuantitativa continua.

3. PRIMERA HIPÓTESIS
• RELACIÓN DEL SEXO CON LA ALTURA
Hipótesis nula: El sexo no condiciona la altura de los sujetos
Hipótesis alternativa: El sexo sí condiciona la altura de los sujetos.

4. Seleccionamos “Analizar” en la barra superior. Clicamos en “Estadísticos descriptivos”, y
elegimos la opción de “Explorar”.

5. Seleccionamos “Gráficos”:
- Hacemos click en “gráficos de
normalidad con pruebas” e histograma.
Seleccionamos las variables:
- Introducimos la altura en la lista de
dependientes.
- Introducimos el sexo en la lista de factores
independientes.

6.  El test de T-Student sólo puede usarse con variables dependientes que siguen
una distribución normal.
• Usamos estas pruebas de normalidad para comprobar si la variable elegida
(altura) sigue una distribución normal o no.
• Para muestras de un tamaño menor o de 50 individuos
como esta, elegimos la prueba de Shapiro-Wilk:
• Partimos de una hipótesis nula (H0): Los datos
siguen una distribución normal.
• Como el error al rechazar H0 es mayor de 0,05
tanto en hombres como en mujeres, la
aceptamos:
Los datos siguen una distribución normal,
luego podemos usar T-Student.

7. Seleccionamos “Analizar”, y elegimos “Comparar medias”. En este caso, como se trata de dos muestras
independientes (mujeres y hombres), seleccionamos “Prueba T para muestras independientes”.

8. Introducimos las variables
dependiente (de prueba) e
independiente (de
agrupación).
*En la variable “sexo” hay que definir los grupos:
- Grupo 1: Valor 1 (que equivale a “varón” en la matriz)
- Grupo 2: valor 2 (que equivale a “mujer” en la matriz)

9. • Miramos la significación bilateral, es decir, el error que se
comete al rechazar la hipótesis nula (p).
• Al ser p menor de 0,05 rechazamos la H0 y por tanto,
aceptamos la hipótesis alternativa:
La altura sí depende del sexo.

10. SEGUNDA HIPÓTESIS
• RELACIÓN DEL SEXO CON EL PESO
Hipótesis nula: El sexo no condiciona el peso de los sujetos
Hipótesis alternativa: El sexo sí condiciona el peso de los sujetos.

11. Seleccionamos las variables:
- Introducimos el peso en la lista de
dependientes.
- Introducimos el sexo en la lista de factores
(independientes)
Seleccionamos “Gráficos”:
- Hacemos click en “gráficos de
normalidad con pruebas” e histograma.

12. • Usamos estas pruebas de normalidad para comprobar si la variable elegida
(peso) sigue una distribución normal o no.
• De nuevo, elegimos la prueba de Shapiro-Wilk:
• Partimos de una hipótesis nula (H0): Los
datos siguen una distribución normal.
• Como el error al rechazar H0 es mayor de
0,05 tanto en hombres como en mujeres, la
aceptamos:
Los datos siguen una distribución normal,
luego podemos usar T-Student.

13. • Miramos la significación bilateral, es decir, el error que se
comete al rechazar la hipótesis nula (p).
• Al ser p menor de 0,05 rechazamos la H0 y por tanto,
aceptamos la hipótesis alternativa:
El peso sí depende del sexo.