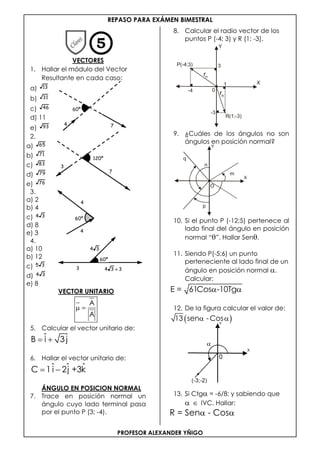
Este documento proporciona un repaso para un examen bimestral sobre vectores y ángulos en posición normal. Contiene 13 problemas de práctica que cubren temas como hallar el módulo de un vector resultante, calcular vectores unitarios, trazar ángulos en posición normal, calcular senos y cosenos de ángulos, y resolver ecuaciones con senos y cosenos. El documento proporciona ejercicios de práctica sobre conceptos clave de vectores y ángulos para prepararse para un examen.

1. REPASO PARA EXÁMEN BIMESTRAL
PROFESOR ALEXANDER YÑIGO
0
Y
X
r
r
P
R
P(-4;3)
R(1;-3)
3
1
-3
-4
Y
X
O
q
n
p
m
VECTORES
1. Hallar el módulo del Vector
Resultante en cada caso:
a) 13
b) 31
c) 46
d) 11
e) 93
2.
a) 65
b) 71
c) 83
d) 79
e) 76
3.
a) 2
b) 4
c) 3
4
d) 8
e) 3
4.
a) 10
b) 12
c) 3
5
d) 3
4
e) 8
VECTOR UNITARIO
A
A
 
5. Calcular el vector unitario de:
B i 3j
 
6. Hallar el vector unitario de:
C 1i 2j +3k
 
ÁNGULO EN POSICION NORMAL
7. Trace en posición normal un
ángulo cuyo lado terminal pasa
por el punto P (3; -4).
8. Calcular el radio vector de los
puntos P (-4; 3) y R (1; -3).
9. ¿Cuáles de los ángulos no son
ángulos en posición normal?
10. Si el punto P (-12;5) pertenece al
lado final del ángulo en posición
normal “”. Hallar Sen.
11. Siendo P(-5;6) un punto
perteneciente al lado final de un
ángulo en posición normal .
Calcular:
E = 61Cos -10Tg
 
12. De la figura calcular el valor de:
 
13 sen - Cos
 
13. Si Ctg = -6/8; y sabiendo que
  IVC. Hallar:
R = Sen - Cos
60º
4 7
120º
3
7
4
4
60º
3
4
3
3
4 
60º
3