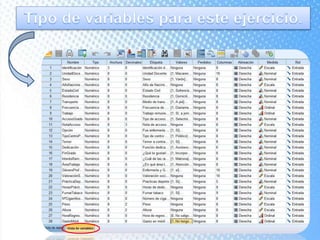
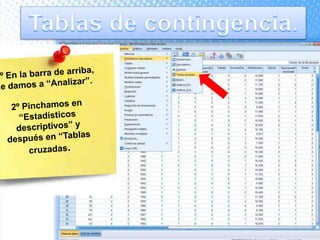
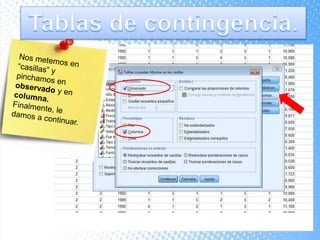
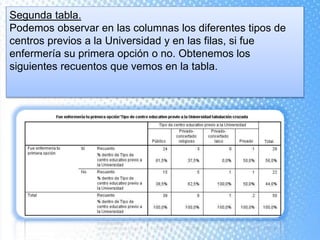
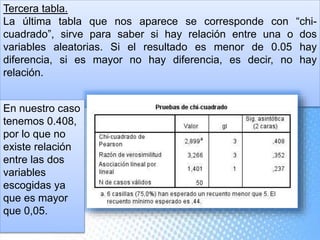
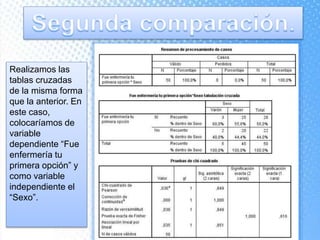
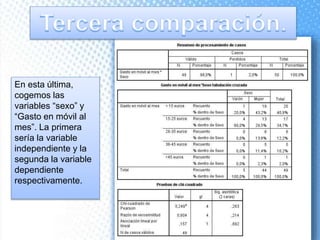
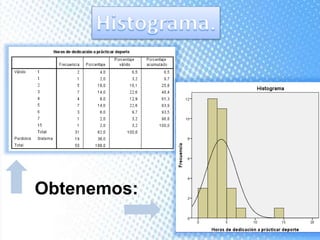
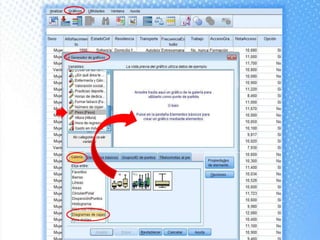
Este documento explica cómo realizar tablas de contingencia y representaciones gráficas para analizar la relación entre variables. Se crean tablas cruzadas y se usa la prueba chi-cuadrado para determinar si existe una relación entre dos variables, como el tipo de centro educativo y la elección de enfermería. Los gráficos incluyen diagramas de sectores, barras, histograma con curva normal y diagrama de cajas para visualizar variables nominales, ordinales y de escala.

1. Tablas de contingencia y
representaciones gráficas.
Sonia Fuentes Graciano.

4. ¿En qué consiste?
Tenemos que realizar las tablas de contingencia para
obtener información acerca de:
¿Existe relación entre el tipo de centro educativo de
donde proviene el alumnado y la opción de elegir
enfermería como primera opción?
¿Existe relación entre elegir enfermería como primera
opción y el sexo del alumnado?
¿Existe relación entre el gasto de móvil mensual y el
sexo?

6. Nos aparece este
cuadro con las distintas
variables para escoger
las dos que nos
interesan. En las
columnas siempre
colocamos las
variables
“independientes”, las
que influyen sobre
otras, y en las filas, las
variables
“dependientes”.
Para desplazar la variable a la fila o a la
columna, tenemos que seleccionarla y
pulsar una de las flechas, dependiendo de
donde queramos colocarla.

8. Nos metemos en
“Estadísticos” y clicamos
en “chi-cuadrado” para que
nos aparezca en las
tablas. Pulsamos
continuar.

9. Primera tabla.
Podemos observar el “resumen de procesamientos de
casos”, es decir, el número de casos y los porcentajes
válidos, perdidos y el recuento total.
¿Existe relación entre el tipo de centro educativo de donde
proviene el alumnado y la opción de elegir enfermería
como primera opción?

10. Primera comparación.
Segunda tabla.
Podemos observar en las columnas los diferentes tipos de
centros previos a la Universidad y en las filas, si fue
enfermería su primera opción o no. Obtenemos los
siguientes recuentos que vemos en la tabla.

11. Tercera tabla.
La última tabla que nos aparece se corresponde con “chi-
cuadrado”, sirve para saber si hay relación entre una o dos
variables aleatorias. Si el resultado es menor de 0.05 hay
diferencia, si es mayor no hay diferencia, es decir, no hay
relación.
En nuestro caso
tenemos 0.408,
por lo que no
existe relación
entre las dos
variables
escogidas ya
que es mayor
que 0,05.

12. Realizamos las
tablas cruzadas
de la misma forma
que la anterior. En
este caso,
colocaríamos de
variable
dependiente “Fue
enfermería tu
primera opción” y
como variable
independiente el
“Sexo”.

13. ¿Existe relación entre elegir enfermería como primera
opción y el sexo del alumnado?
Como vemos en la primera tabla de la diapositiva
anterior, han contestado las 50 personas a las
que se ha realizado el estudio, por lo tanto, no
hay casos perdidos.
En la segunda, vemos el recuento de los datos.
Hay más mujeres que eligieron enfermería de
primera opción que hombres, pero también
ganan las mujeres en el caso contrario ya que
en el estudio sólo hay cinco hombres.
En la tercera, que se corresponde con el chi-
cuadrado, vemos que el resultado es 0,616
(mayor que 0,05) por lo que no hay relación
entre elegir enfermería como primera opción y el
sexo.

14. En esta última,
cogemos las
variables “sexo” y
“Gasto en móvil al
mes”. La primera
sería la variable
independiente y la
segunda la variable
dependiente
respectivamente.

15. ¿Existe relación entre el gasto de móvil mensual y el
sexo?
En el resumen de procedimientos
de casos, vemos que sólo hay un
caso perdido.
En la segunda tabla observamos
que las mujeres suelen gastar más
que los hombres en el móvil. Muy
pocos sobrepasan los 35 euros.
El chi-cuadrado en este caso
también es mayor de 0,05, por lo
que no existe relación entre el
gasto en móvil al mes y el sexo.

16. ¿En qué consiste?
Representar gráficamente:
 Dos variables nominales. Una en diagrama de sector
y otra en barras.
Una variable ordinal en diagramas de barras.
Una variable en escala en histograma y con curva de
normalidad.
Una variable de escala en diagrama de caja.

17. Para realizar esta
actividad, 1º
pinchamos en
“analizar”,
“Estadísticos
descriptivos” y
“Frecuencias”.
2º Escogemos la
variable que
queramos, en este
caso, hemos elegido
la variable “Sexo”.
3º pinchamos en
gráficos (elegimos el
que queramos
realizar), frecuencias
y le damos a
continuar.

19. Con los mismos
pasos que realizamos
anteriormente para
hacer el diagrama de
sectores, hacemos el
de barras. Hemos
escogido otra
variable nominal,
“Ciudad de
residencia” y se
representa
gráficamente así:

20. Variable “Hora de regreso a casa después de la fiesta”.
Representación en diagrama de barras.

21. I. Escogemos una
variable de escala,
“Hora de dedicación a
practicar deporte”.
II. Pinchamos en
“Gráficos” y
escogemos el tipo de
gráfico que queramos
realizar en este caso,
histograma.
 Mostrar curva
normal en el
histograma.
III. Le damos a continuar.

22. Obtenemos:

23. Para realizar un diagrama de cajas nos metemos en
“Gráficos”.
“Generador de gráficos” Seleccionamos el tipo
de gráfico que queremos en galería (Diagrama de cajas)
Elegimos la variable que queremos representar como por
ejemplo el peso, ya que tiene que ser de tipo escala
Arrastramos el gráfico hacia arriba, y colocamos en el eje Y
la variable dependiente (Peso) y el eje X la variable
independiente (Sexo).

27. Interpretación de la gráfica.
Como nos muestra el diagrama, el peso máximo de los
hombres de este estudio se encuentra en los 100Kg, y el
mínimo sobre los 70Kg. El peso medio de los hombres
se encuentra entre los 75Kg.
En el caso de las mujeres, el peso máximo está casi en
los 60Kg y el mínimo en 38Kg aproximadamente. El
peso medio en mujeres está sobre los 58Kg.