El documento presenta un análisis estadístico de variables cualitativas y cuantitativas de una muestra de 286 madres y 283 padres. Se analizan variables como el nivel de estudios, horas de deporte, peso y altura. Los resultados muestran que aproximadamente el 50% de las madres y el 40% de los padres no tienen estudios o solo estudios primarios, y que la mayoría de la muestra practica entre 0 y 4 horas de deporte a la semana y pesa entre 40 y 70 kg.

1. Seminario 6

2. ACTIVIDAD 1 :
Analizar variables cualitativas.

3. La primera variable que he escogido es el grado de estudio de las madres, en ella
podemos observar cómo el total de participantes de 286 madres de las que
aproximadamente el 50% de ellas no tienen ningún estudio o sólo los primarios; por
otro lado, vemos cómo predomina las madres que han cursado bachillerato frente a
las universitarias , quedando en el último lugar los estudios universitarios.
counts:
estudiosmadre
Ninguno o primarios Bachiller Universitarios
135 82 69
percentages:
estudiosmadre
Ninguno o primarios Bachiller Universitarios
47.20 28.67 24.13

4. En segundo lugar, he escogido la variable de estudios de los padres.
El total de la muestra estudiada es de 283 padres en el que alrededor del 40% no tienen
ningún estudio o sólo los primarios mucho menor al de las madres; también , predomina el
bachiller frente a los estudios universitarios el cual se vuelve a quedar en último lugar.
En definitiva, en comparación con la anterior variable podemos decir que existe un mayor
número de hombres con estudios superiores y primarios que mujeres.
Counts:
estudiospadre
Ninguno o primarios Bachiller Universitarios
108 93 82
percentages:
estudiospadre
Ninguno o primarios Bachiller Universitarios
38.16 32.86 28.98

5. ACTIVIDAD 2:
Variables cuantitativas.

6. En primer lugar, he elegido las horas en las que
se práctica deporte así: vemos cómo la Media
es de 2 horas y media y la Mediana de 2 horas,
son números muy cercanos por lo que
podemos decir que es un estudio bastante
simétrico.
Por otro lado, podemos observar cómo la
diferencia entre el primer cuartil y el segundo
; y , a su vez entre el segundo y el tercero es
prácticamente similar por lo que al mismo
tiempo de ser simétrica es homogénea.
Para finalizar, vemos que la desviación
estándar es mayor que la media por lo que
podemos concluir que cifras más extremas
influyen en la media por lo que no sería muy
representativa.
horapracticadeportiva escalaas
Min. : 0.000 Min. :28.00
1st Qu.: 0.000 1st Qu.:46.00
Median : 2.000 Median :51.00
Mean : 2.483 Mean :50.71
3rd Qu.: 4.000 3rd Qu.:56.00
Max. :16.000 Max. :72.00
NA's :1 NA's :110
> library(abind, pos=18)
> library(e1071, pos=19)
> numSummary(Datos[,"horapracticadeportiva"],
statistics=c("mean", "sd", "IQR", "quantiles"),
+ quantiles=c(0,.25,.5,.75,1))
mean sd IQR 0% 25% 50% 75% 100% n NA
2.482759 3.138616 4 0 0 2 4 16 290 1

7. En segundo lugar, he escogido la altura:
En ella podemos ver cómo la media es de 1,667 y la mediana de 1,61 no
existe una gran diferencia por lo que podemos decir que el estadístico es
probablemente simétrico; por otro lado, la desviación típica es pequeña
cosa que nos índica que la Media es bastante representativa por lo que en
general respecta y por lo tanto los valores extremos no la influencia.
La diferencia entre el primer cuartil y el segundo y este y el tercero es un
poco mayor en el primero por lo que podemos decir que se encuentra más
homogeneizado entre el 50% y el 75%.
Para finalizar, observamos que la desviación típica es pequeña por lo que
podemos decir que la media es bastante representativa.
> numSummary(Datos[,"altura"], statistics=c("mean",
"sd", "IQR", "quantiles"), quantiles=c(0,
+ .25,.5,.75,1))
mean sd IQR 0% 25% 50% 75% 100% n NA
1.667 0.08078101 0.12 1.46 1.6 1.655 1.72 2 290

8. ACTIVIDAD 3:
Gráficos.

9. En este gráfico vemos
representado la variable
sexo(variable cualitativa) en
la que podemos ver cómo la
gran mayoría de la muestra
son mujeres ; mientras que
los hombres se encuentran
en menor proporción.
GRÁFICO DE SECTORES.

10. DIAGRAMA DE BARRAS:
En el diagrama de barrar se encuentra
expuesto el consumo de dulces(variable
cualitativa), el cual podemos ver cómo la
mayoría de la muestra consume dulces
menos de una vez a la semana, detrás le
sigue 1 o 2 veces a la semana; por otro
lado, el consumo diario de dulce se
produce en menor frecuencia que nunca
y que el consumo de dulce de 3 o más
veces a la semana.

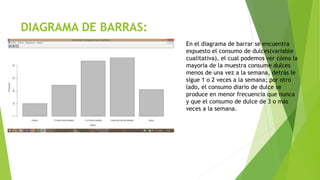
11. HISTOGRAMA:
>numSummary(Datos[,"escalaas"],
statistics=c("mean", "sd", "IQR", "quantiles"),
+ quantiles=c(0,.25,.5,.75,1))
mean sd IQR 0% 25% 50% 75% 100% n NA
50.70994 8.469233 10 28 46 51 56 72 181 110
 En este histograma hemos representado la variable Escalas (variable cuantitativa) en la que se
representa la suma de otras variables como por ejemplo cerveza, dulces,verduras.. Cuanto mayor
sea la puntuación más saludable es la vida de la persona.
 En él podemos ver cómo la media de la muestra tiene una puntuación media por lo que podemos
decir que la gran mayoría lleva una vida saludable generalmente y, además la mediana es
parecida a la media así que la muestra se podría decir que es simétrica.

12. DIAGRAMA DE CAJAS:En este gráfico vemos expuesta la
variable peso(variable cuantitativa) en el
que el rango de peso estudiado se
encuentra entre 90kg y 40kg
respectivamente.
La mediana se encuentra entorno a 60kg
y también observamos que el 50% de la
muestra pesa entre 70 -55 kg.
Por otro lado, vemos como en el primer
cuartil la muestra está más concentrada
que en el tercer cuartil.
Otros datos interesantes son :
- 25% entre 40-55kg.
- 50% entre 40-60kg.
-25% entre 70-90kg.
- 75% entre 40-70kg.
Tras ello, podemos decir que la gran
mayoría se encuentra comprendido entre
los 40 y los 70kg.
Por último, existen valores extremos que
influencia en la muestra.