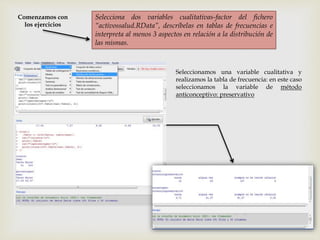
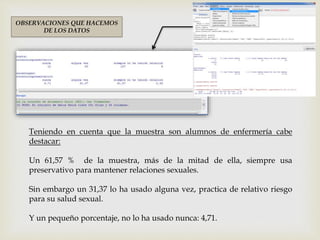
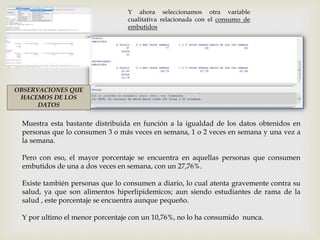
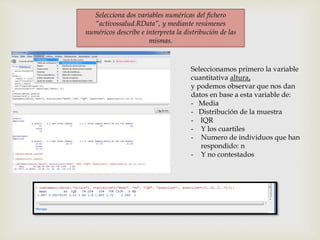
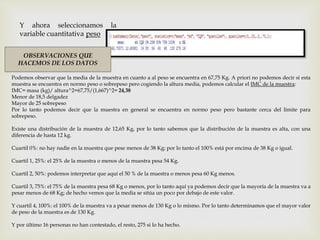
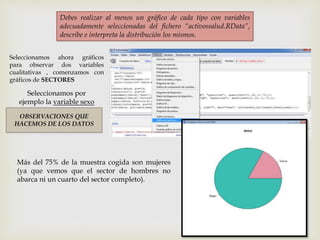
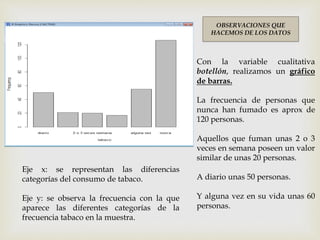
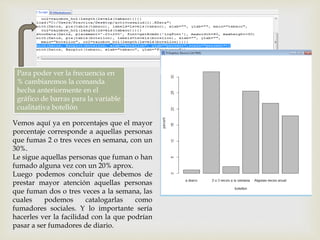
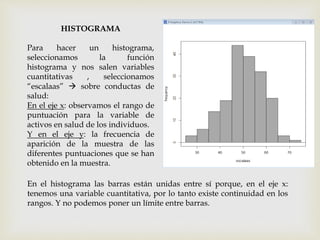
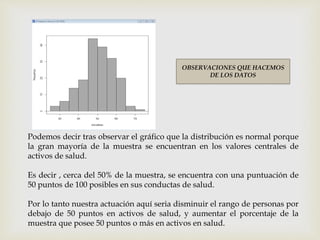
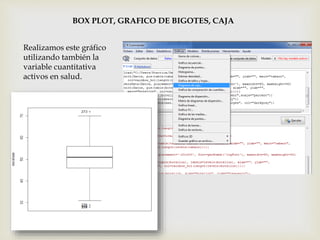
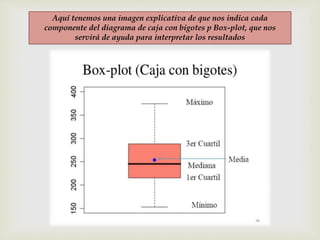
Este documento presenta los pasos para analizar variables cualitativas y cuantitativas de un conjunto de datos usando tablas de frecuencia, resúmenes numéricos, gráficos de sectores, barras e histograma. Se analizan variables como método anticonceptivo, consumo de embutidos, altura, peso y conductas de salud. La mayoría de la muestra usa preservativo y consume embutidos 1-2 veces por semana. La altura promedio es 1.667m y el peso promedio es 67.75kg. Los gráficos muestran

1. 
SEMINARIO 6

2. Seleccionamos una variable cualitativa y
realizamos la tabla de frecuencia: en este caso
seleccionamos la variable de método
anticonceptivo: preservativo
Selecciona dos variables cualitativas-factor del fichero
“activossalud.RData”, descríbelas en tablas de frecuencias e
interpreta al menos 3 aspectos en relación a la distribución de
las mismas.
Comenzamos con
los ejercicios

3. Teniendo en cuenta que la muestra son alumnos de enfermería cabe
destacar:
Un 61,57 % de la muestra, más de la mitad de ella, siempre usa
preservativo para mantener relaciones sexuales.
Sin embargo un 31,37 lo ha usado alguna vez, practica de relativo riesgo
para su salud sexual.
Y un pequeño porcentaje, no lo ha usado nunca: 4,71.
OBSERVACIONES QUE HACEMOS
DE LOS DATOS

4. Y ahora seleccionamos otra variable
cualitativa relacionada con el consumo de
embutidos
OBSERVACIONES QUE
HACEMOS DE LOS
DATOS
Muestra esta bastante distribuida en función a la igualdad de los datos obtenidos en
personas que lo consumen 3 o más veces en semana, 1 o 2 veces en semana y una vez a
la semana.
Pero con eso, el mayor porcentaje se encuentra en aquellas personas que consumen
embutidos de una a dos veces en semana, con un 27,76%.
Existe también personas que lo consumen a diario, lo cual atenta gravemente contra su
salud, ya que son alimentos hiperlipidemicos; aun siendo estudiantes de rama de la
salud , este porcentaje se encuentra aunque pequeño.
Y por ultimo el menor porcentaje con un 10,76%, no lo ha consumido nunca.

5. Selecciona dos variables numéricas del fichero
“activossalud.RData”, y mediante resúmenes
numéricos describe e interpreta la distribución de las
mismas.
Seleccionamos primero la variable
cuantitativa altura,
y podemos observar que nos dan
datos en base a esta variable de:
- Media
- Distribución de la muestra
- IQR
- Y los cuartiles
- Numero de individuos que han
respondido: n
- Y no contestados

6. OBSERVACIONES QUE
HACEMOS DE LOS DATOS
Podemos observar que la media de la muestra en cuanto a la altura es de 1,667 m , así aquí agrupamos
todos los valores de medida y al ver que la distribución de la muestra es pequeñas, podemos decir que
la mayoría de la muestra medirá más o menos 1,667m.
Existe una distribución de la muestra de 0.080 m, que es muy pequeña, por lo tanto los valores de la
muestra en cuanto a la altura no difieren mucho uno de otros.
Cuartil 0%: no hay nadie en la muestra que mida menos de 1,46 m ; por lo tanto el 100% está por
encima de 1,46 m o igual.
Cuartil 1, 25%: el 25% de la muestra o menos de la muestra mide 1,60 m.
Cuartil 2, 50%: podemos interpretar que aquí el 50 % de la muestra o menos mide 1.655 m o menos.
Cuartil 3, 75%: el 75% de la muestra mide 1,72 m o menos, por lo tanto aquí ya podemos decir que la
mayoría de la muestra va a medir menos de 1,72 m ; de hecho vemos que la media se sitúa en 1,667m .
Y cuartil 4, 100%: el 100% de la muestra va a medir menos de dos metros. Por lo tanto concluimos que
nadie de la muestra mide dos metros.
Y solo una persona no nos ha contestado al respecto de su altura.

7. Y ahora seleccionamos la
variable cuantitativa peso
OBSERVACIONES QUE
HACEMOS DE LOS DATOS
Podemos observar que la media de la muestra en cuanto a al peso se encuentra en 67,75 Kg. A priori no podemos decir si esta
muestra se encuentra en normo peso o sobrepeso pero cogiendo la altura media, podemos calcular el IMC de la muestra:
IMC= masa (kg)/ altura^2=67,75/(1,667)^2= 24,38
Menor de 18,5 delgadez
Mayor de 25 sobrepeso
Por lo tanto podemos decir que la muestra en general se encuentra en normo peso pero bastante cerca del límite para
sobrepeso.
Existe una distribución de la muestra de 12,65 Kg, por lo tanto sabemos que la distribución de la muestra es alta, con una
diferencia de hasta 12 kg.
Cuartil 0%: no hay nadie en la muestra que pese menos de 38 Kg; por lo tanto el 100% está por encima de 38 Kg o igual.
Cuartil 1, 25%: el 25% de la muestra o menos de la muestra pesa 54 Kg.
Cuartil 2, 50%: podemos interpretar que aquí el 50 % de la muestra o menos pesa 60 Kg menos.
Cuartil 3, 75%: el 75% de la muestra pesa 68 Kg o menos, por lo tanto aquí ya podemos decir que la mayoría de la muestra va a
pesar menos de 68 Kg; de hecho vemos que la media se sitúa un poco por debajo de este valor.
Y cuartil 4, 100%: el 100% de la muestra va a pesar menos de 130 Kg o lo mismo. Por lo tanto determinamos que el mayor valor
de peso de la muestra es de 130 Kg.
Y por último 16 personas no han contestado, el resto, 275 si lo ha hecho.

8. Debes realizar al menos un gráfico de cada tipo con variables
adecuadamente seleccionadas del fichero “activossalud.RData”,
describe e interpreta la distribución los mismos.
Seleccionamos ahora gráficos
para observar dos variables
cualitativas , comenzamos con
gráficos de SECTORES
Seleccionamos por
ejemplo la variable sexo
OBSERVACIONES QUE
HACEMOS DE LOS DATOS
Más del 75% de la muestra cogida son mujeres
(ya que vemos que el sector de hombres no
abarca ni un cuarto del sector completo).

9. Cogemos ahora la variable
cualitativa tabaco:
Casi la mitad de la muestra no ha
fumado nunca, sin embargo el
gráfico es muy similar para 2 o 3
veces en semana, 2 o 3 veces al mes y
fines de semana; luego observamos
que aquí el grafico pierde utilidad
porque dicha variable posee muchas
categorías y dichos valores obtenidos
son muy similares.
¡Por lo tanto para variables de más
de dos categorías no es recomendable
usar gráficos de sectores!

10. Con la variable cualitativa
botellón, realizamos un gráfico
de barras.
La frecuencia de personas que
nunca han fumado es aprox de
120 personas.
Aquellos que fuman unas 2 o 3
veces en semana poseen un valor
similar de unas 20 personas.
A diario unas 50 personas.
Y alguna vez en su vida unas 60
personas.
Eje x: se representan las diferencias
categorías del consumo de tabaco.
Eje y: se observa la frecuencia con la que
aparece las diferentes categorías de la
frecuencia tabaco en la muestra.
OBSERVACIONES QUE
HACEMOS DE LOS DATOS

11. Para poder ver la frecuencia en
% cambiaremos la comanda
hecha anteriormente en el
gráfico de barras para la variable
cualitativa botellón
Vemos aquí ya en porcentajes que el mayor
porcentaje corresponde a aquellas personas
que fumas 2 o tres veces en semana, con un
30%.
Le sigue aquellas personas que fuman o han
fumado alguna vez con un 20% aprox.
Luego podemos concluir que debemos de
prestar mayor atención aquellas personas
que fuman dos o tres veces a la semana, las
cuales podemos catalogarlas como
fumadores sociales. Y lo importante sería
hacerles ver la facilidad con la que podrían
pasar a ser fumadores de diario.

12. HISTOGRAMA
Para hacer un histograma,
seleccionamos la función
histograma y nos salen variables
cuantitativas , seleccionamos
“escalaas”  sobre conductas de
salud:
En el eje x: observamos el rango de
puntuación para la variable de
activos en salud de los individuos.
Y en el eje y: la frecuencia de
aparición de la muestra de las
diferentes puntuaciones que se han
obtenido en la muestra.
En el histograma las barras están unidas entre sí porque, en el eje x:
tenemos una variable cuantitativa, por lo tanto existe continuidad en los
rangos. Y no podemos poner un límite entre barras.

13. OBSERVACIONES QUE HACEMOS
DE LOS DATOS
Podemos decir tras observar el gráfico que la distribución es normal porque
la gran mayoría de la muestra se encuentran en los valores centrales de
activos de salud.
Es decir , cerca del 50% de la muestra, se encuentra con una puntuación de
50 puntos de 100 posibles en sus conductas de salud.
Por lo tanto nuestra actuación aquí seria disminuir el rango de personas por
debajo de 50 puntos en activos de salud, y aumentar el porcentaje de la
muestra que posee 50 puntos o más en activos en salud.

14. BOX PLOT, GRAFICO DE BIGOTES, CAJA
Realizamos este gráfico
utilizando también la
variable cuantitativa
activos en salud.

15. Aquí tenemos una imagen explicativa de que nos indica cada
componente del diagrama de caja con bigotes p Box-plot, que nos
servirá de ayuda para interpretar los resultados

16. OBSERVACIONES QUE HACEMOS
DE LOS DATOS
La caja representa el 50% de la muestra;
es decir, la distribución que presentan
los valores del 50% de la muestra. Que
como vemos aquí se encuentran entre
una puntuación de 45-55 de activos en
salud.
El otro 50% de la muestra queda
distribuido de la siguiente forma:
- El 25% desde el borde superior de la
caja hasta el valor máximo de activos
en salud (70).
- El otro 25% desde el borde inferior
de la caja hasta el valor mínimo de
activos en salud recogidos (28
aprox).
El rango intercuartílico se representa
desde la línea inferior de la caja a la
línea superior.
La mediana se encuentra también
alrededor del valor 50 en activos en
salud.
La media se encuentra alrededor del
valor 50 de los activos en salud.
Hay dos valores atípicos que son 226 y 288
por debajo y un valor atípico por encima que
es de 273.
Pero en general la muestra es normal porque
la media y la mediana de la muestra se
encuentran alrededor del valor 50 de los
activos en salud.