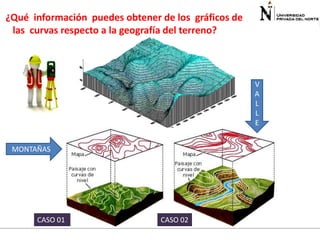
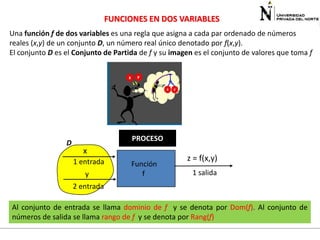
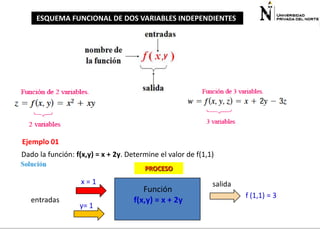
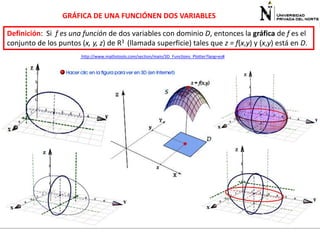
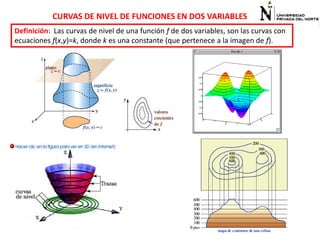
El documento presenta información sobre funciones de varias variables en el contexto de cálculo 3. Explica cómo las curvas de nivel en gráficos topográficos pueden proporcionar información sobre la geografía del terreno. Luego define funciones de dos variables, sus dominios y rangos, y presenta ejemplos para ilustrar conceptos como álgebra y gráficas de funciones de varias variables. Finalmente, introduce curvas de nivel y cómo calcular el dominio de una función.

1. CÁLCULO 3
Departamento de Ciencias
Juan Carlos Broncano Torres

2. ¿Qué información puedes obtener de los gráficos de
las curvas respecto a la geografía del terreno?
V
A
L
L
E
MONTAÑAS
CASO 01
CASO 02

3. Modelos matemáticos para explicar patrones
topográficos
Un levantaminto topográfico es um conjunto de operaciones con a finalidad de determinar
la posición relativa de puntos en una superfície terrestre.
Existen Muchas formas de realizar un
levantamiento topográfico . Una de estas
formas se llama método de intersección
directa y lateral, el cual presenta un
problema; que consiste en saber
determinar apropiadamente las
coordenadas de un punto después de
triangularizar el terreno.
Se ha concluido Matemáticamente que las
coordenadas de dicho se puede
determinar mediante las relaciones:

4. Logros de la sesión:
Al finalizar la sesión, el estudiante resuelve problemas vinculados a
gestión e ingeniería a partir de funciones de varias variables,
usando el cálculo de su dominio en forma
analítica, e
interpretando sus curvas de nivel en forma gráfica.

5. FUNCIONES EN DOS VARIABLES
Una función f de dos variables es una regla que asigna a cada par ordenado de números
reales (x,y) de un conjunto D, un número real único denotado por f(x,y).
El conjunto D es el Conjunto de Partida de f y su imagen es el conjunto de valores que toma f
D
PROCESO
x
1 entrada
y
Función
f
z = f(x,y)
1 salida
2 entrada
Al conjunto de entrada se llama dominio de f y se denota por Dom(f). Al conjunto de
números de salida se llama rango de f y se denota por Rang(f)

6. ESQUEMA FUNCIONAL DE DOS VARIABLES INDEPENDIENTES
Ejemplo 01
Dado la función: f(x,y) = x + 2y. Determine el valor de f(1,1)
PROCESO
x=1
entradas
y= 1
Función
f(x,y) = x + 2y
salida
f (1,1) = 3

7. Ejemplo 02
¿Indique la expresión matemática que represente el área de un rectángulo?
Variables
independientes
A(x,y) = x.y
Variable
dependiente
Ejemplo 03:
La niebla de un aeropuerto se puede despejar si se calienta el aire. Si la cantidad de calor requerido,
es: H = T/w + w/T (en calorías por metro cúbico de niebla),
donde T (en °C) representa la temperatura del aire, y, w la humedad de la niebla (en gramos por
metro cúbico de niebla).
• ¿H es una función de T y w ?
•¿Indique la (o las) variable dependiente?
•¿Indique la (o las) variables independientes?

8. ÁLGEBRA DE FUNCIONES EN DOS VARIABLES

9. GRÁFICA DE UNA FUNCIÓNEN DOS VARIABLES
Definición: Si f es una función de dos variables con dominio D, entonces la gráfica de f es el
conjunto de los puntos (x, y, z) de R3 (llamada superficie) tales que z = f(x,y) y (x,y) está en D.
http://www.mathstools.com/section/main/3D_Functions_Plotter?lang=es#

10. CÁLCULO DE DOMINIO DE UNA FUNCIÓN EN DOS VARIABLES
Es un procedimiento algebraico que consiste en determinar analíticamente
el conjunto de pares ordenados para los cuales la función esta definida

11. A PRACTICAR
1.-
2.- Halle en cada caso lo pedido:
3.- Halle el dominio de cada una de las siguientes funciones:
a) f ( x, y)
4.-
x
xy
b) f ( x, y) ln( x / y)
c) f ( x, y)
x
25 x 2
y2

12. CURVAS DE NIVEL DE FUNCIONES EN DOS VARIABLES
Definición: Las curvas de nivel de una función f de dos variables, son las curvas con
ecuaciones f(x,y)=k, donde k es una constante (que pertenece a la imagen de f).

13. Ejemplo
Ejemplo

14. A PRACTICAR
1.-
Recuerda… :

15. Mercado de Capitales
La tabla muestra las ventas netas x (en miles de millones de dólares), los activos totales y
(en miles de millones de dólares) y los derechos de los accionistas z (en miles de millones de
dólares) de Wal-Mart desde 2002 hasta el 2007.
(Fuente: 2007 Annual Report for Wal-Mart)
Un modelo para estos datos es:
a) Utilizar una herramienta de graficación y el modelo para aproximar z para los valores
dados de x y y.
b) ¿Cuál de las dos variables en este modelo tiene mayor influencia sobre los derechos de
los accionistas?
c) Simplificar la expresión de f (x, 95) e interpretar su significado en el contexto del
problema.

16. BIBLIOGRAFÍA
#
CÓDIGO
AUTOR
TÍTULO
EDITORIAL
1
515.33
PURC
PURCELL,
EDWIN J.
Cálculo Diferencial E
Integral
Pearson
Educación
2
515
STEW/M
2002
STEWART,
JAMES
Cálculo
Multivariable
Cuarta edición,
Mexico 2001,
Edit. Thomson
Cálculo Aplicado Para
Administración,
Economía Y Ciencias
Sociales
Octava edición,
México
2007,.Mcgrawhill
3
515 HOFF/C HOFFMANN,
2006
LAURENCE D.