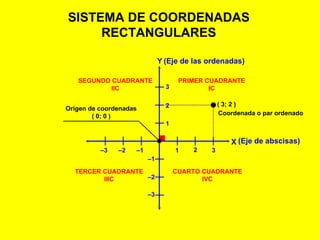
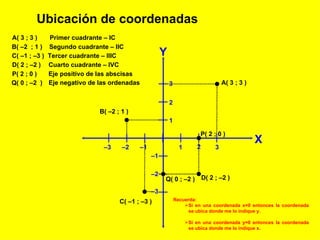
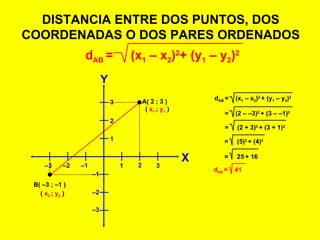
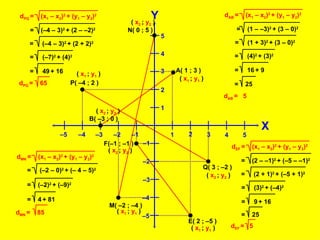
El documento describe el sistema de coordenadas rectangulares, incluyendo sus cuatro cuadrantes, ejes y cómo ubicar puntos usando coordenadas. Explica cómo calcular la distancia entre dos puntos usando la fórmula que involucra restar las coordenadas x e y de los puntos y elevar los resultados al cuadrado y sumarlos.

1. SISTEMA DE COORDENADAS RECTANGULARES PRIMER CUADRANTE IC SEGUNDO CUADRANTE IIC TERCER CUADRANTE IIIC CUARTO CUADRANTE IVC X Y (Eje de abscisas) (Eje de las ordenadas) ( 3; 2 ) Coordenada o par ordenado 1 2 – 3 – 2 – 1 3 1 2 3 – 1 – 2 – 3 Origen de coordenadas ( 0; 0 )

2. ¿QUÉ ES UN SISTEMA DE COORDENADAS RECTANGULARES? PARTES DE UN PLANO CARTESIANO O PLANO DE COORDENADAS Es un sistema formado por dos rectas numéricas que se cortan perpendicularmente en su origen(una horizontal y otra vertical, además ambas rectas tienen la misma unidad de distancia) Ejes Eje de abscisas (X) Eje de ordenadas (Y) Cuadrantes Primer cuadrante ( IC ) Segundo cuadrante ( IIC ) Tercer cuadrante ( IIIC ) Cuarto cuadrante ( IVC ) Par ordenado o coordenada

3. Ubicación de coordenadas P( 2 ; 0 ) Q( 0 ; –2 ) B( –2 ; 1 ) A( 3 ; 3 ) B( –2 ; 1 ) C( –1 ; –3 ) P( 2 ; 0 ) Q( 0 ; –2 ) A( 3 ; 3 ) C( –1 ; –3 ) Recuerda: Si en una coordenada x=0 entonces la coordenada se ubica donde me lo indique y. Si en una coordenada y=0 entonces la coordenada se ubica donde me lo indique x. Primer cuadrante – IC Segundo cuadrante – IIC Tercer cuadrante – IIIC D( 2 ; –2 ) Cuarto cuadrante – IVC D( 2 ; –2 ) Eje positivo de las abscisas Eje negativo de las ordenadas 1 2 3 – 1 – 2 – 3 1 2 – 3 – 2 – 1 3 X Y

4. DISTANCIA ENTRE DOS PUNTOS, DOS COORDENADAS O DOS PARES ORDENADOS A( 2 ; 3 ) B( –3 ; –1 ) ( x 1 ; y 1 ) ( x 2 ; y 2 ) X Y 1 2 – 3 – 2 – 1 3 1 2 3 – 1 – 2 – 3 d AB = (x 1 – x 2 ) 2 + (y 1 – y 2 ) 2 d AB = (x 1 – x 2 ) 2 + (y 1 – y 2 ) 2 = (2 – –3) 2 + (3 – –1) 2 = (2 + 3) 2 + (3 + 1) 2 = (5) 2 + (4) 2 = 25 + 16 d AB = 41

5. F(–1 ; –1 ) A( 1 ; 3 ) B( –3 ; 0 ) ( x 1 ; y 1 ) ( x 2 ; y 2 ) d AB = 5 P( –4 ; 2 ) N( 0 ; 5 ) ( x 2 ; y 2 ) M( –2 ; –4 ) ( x 1 ; y 1 ) ( x 1 ; y 1 ) Q( 3 ; –2 ) ( x 2 ; y 2 ) E( 2 ; –5 ) ( x 1 ; y 1 ) ( x 2 ; y 2 ) – 1 X 1 2 3 – 1 – 2 – 3 4 5 – 4 – 5 Y – 3 – 2 1 2 3 – 4 – 5 4 5 d AB = (x 1 – x 2 ) 2 + (y 1 – y 2 ) 2 = (1 – –3) 2 + (3 – 0) 2 = (1 + 3) 2 + (3 – 0) 2 = (4) 2 + (3) 2 = 16 + 9 = 25 d EF = (x 1 – x 2 ) 2 + (y 1 – y 2 ) 2 = (2 – –1) 2 + (–5 – –1) 2 = (2 + 1) 2 + (–5 + 1) 2 = (3) 2 + (–4) 2 = 9 + 16 d EF = 5 = 25 d PQ = (x 1 – x 2 ) 2 + (y 1 – y 2 ) 2 = (–4 – 3) 2 + (2 – –2) 2 = (–4 – 3) 2 + (2 + 2) 2 = (–7) 2 + (4) 2 = 49 + 16 d PQ = 65 d MN = (x 1 – x 2 ) 2 + (y 1 – y 2 ) 2 = (–2 – 0) 2 + (– 4 – 5) 2 = (–2) 2 + (–9) 2 = 4 + 81 d MN = 85