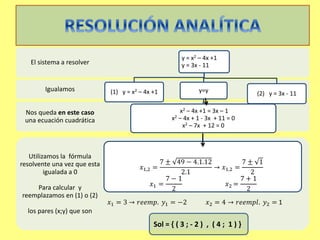
El documento presenta diferentes métodos para resolver sistemas de ecuaciones mixtos. Define un sistema mixto como aquel que contiene al menos una ecuación no lineal. Explica el método analítico, gráfico y por tablas para resolver sistemas. Incluye ejemplos y ejercicios de clasificación y resolución de sistemas mixtos.

1. • DEFINICIÓN
• EJEMPLO Nº1
• SOLUCIÓN POR TABLAS
• METODO ANÁLITICO
• METODO GRÁFICO
• EJERCICIOS
• POBLEMAS

2. Definición:
Se llama sistema mixto a todo
sistema de ecuaciones donde
por lo menos una de las
ecuaciones no es lineal
y= 3x + 7
ejemplo
y= x2 – 5

3. • Dada las funciones:
• f(x)= x2 – 4x +1 (cuadrática)
• g(x)= 3x – 11
• Se obtiene un sistema
y = x2 – 4x +1
•
y = 3x – 11
• Resolver el sistema consiste encontrar los
pares (x;y) que satisface a las dos ecuaciones

4. y = x2 – 4x +1
X Y (X ; Y )
-1 6 (-1;6)
0 1 (0;1)
1 -2 (1,-2)
2 -3 (2;-3)
3 -2 (3;-2)
4 1 (4;1)
5 6 (5;6)
6 13 (6;13)
y = 3x – 11
X Y (X ; Y )
-1 - 14 (-1;-14)
0 - 11 (0;-11)
1 -8 (1;-8)
2 -5 (2;-5)
3 -2 (3;-2)
4 1 (4;1)
5 4 (5;4)
6 7 (6;7)
y = x2 – 4x +1
y = 3x - 11
Por tanto el conjunto solución esta formado por dos pare ordenados
Sol = { ( 3 ; - 2 ) , ( 4 ; 1 ) }

5. Utilizamos la fórmula
resolvente una vez que esta
igualada a 0
Para calcular y
reemplazamos en (1) o (2)
los pares (x;y) que son
Nos queda en este caso
una ecuación cuadrática
Igualamos
El sistema a resolver
y = x2 – 4x +1
y = 3x - 11
(1) y = x2 – 4x +1 y=y
x2 – 4x +1 = 3x – 1
x2 – 4x + 1 - 3x + 11 = 0
x2 – 7x + 12 = 0
(2) y = 3x - 11
𝑥1,2 =
7 ± 49 − 4.1.12
2.1
→ 𝑥1,2 =
7 ± 1
2
𝑥1 =
7 − 1
2
𝑥2 =
7 + 1
2
𝑥1 = 3 → 𝑟𝑒𝑒𝑚𝑝. 𝑦1 = −2 𝑥2 = 4 → 𝑟𝑒𝑒𝑚𝑝𝑙. 𝑦2 = 1
Sol = { ( 3 ; - 2 ) , ( 4 ; 1 ) }

6. Recordemos: la grafica una de
una cuadrática es una: Para representar la lineal lo
haremos por ORDENADA A
ORIGEN y PENDIENTE
• y=x2-4x+1
• Vértice 2; −3
• 𝑥 𝑣=
−𝑏
2𝑎
= 2
• 𝑦𝑣 = 𝑓 2 = −3
• Ordenada al origen
f(0)= 1
• Raíces
• 𝑥1,2 =
−𝑏± 𝑏2−4𝑎𝑐
2𝑎
• 𝑥1 = 𝑥2 =
• y =3x – 11
• Ord. Al Orig.
• b = -11
• Pendiente
• m = 3

7. Ejercicios
Clasifica los siguientes sistemas Resolver analíticamente





32
2
) 2
xxy
xy
e
 





22
22
) 2
2
xxy
xy
a





xy
xxy
b
1
)
2





xy
xxy
f
2
24
)
2





xxy
xxy
c
22
) 2
3





2
3
1
)
xy
xxy
h
Dados los siguientes sistemas mixtos se pide
Resolver el sistema por método analítico
Completar el grafico
Dar el conjunto solución
Clasifica los siguientes sistemas








4
1
2
)
2
xy
x
x
y
g








1
52
1
)
xy
x
x
y
d







1
2
1
)(
32)(
)
xxg
xxf
i

8. Problemas para interpretar plantear y resolver
• Lanzamos un proyectil. La altura alcanzada y (en Km) y
los kilómetros recorridos x están relacionados por la
ecuación y = -2x2 + 4x. A 1 Km del lugar de lanzamiento
se encuentra una montaña cuya ladera oeste sigue la recta
de ecuación y = 6x - 6. Halla el punto de la montaña
donde se producirá el impacto.
• El costo total de producción de “x” unidades de un determinado artículo está
dado por l función 𝐶 𝑥 = 𝑥2
+ 2𝑥 + 360 y los ingresos obtenidos por las venta
por 𝐼 𝑥 = −𝑥2
+ 74𝑥 Se solicita
Graficar las dos funciones en un mismo sistema de ejes cartesianos
¿Cuál son las restricciones que se deben realizar para para que la situación tenga sentido
¿A partir de que cantidad de unidades las costos igualan a las ganancias
Que pasa para cantidades inferiores y para las mayores a la obtenida en el ítem anterior
• Se lanza una pelota hacia arriba y simultáneamente un ave levanta vuelo. La
trayectoria de la pelota se describe mediante la función 𝑦 = −3𝑥2 + 12𝑥 y la de l
vuelo del ave, mediante 𝑦 = 1,5𝑥 + 7,5
Siendo (x;y) las coordenadas de la trayectoria
Graficar las dos funciones en un mismo sistema de ejes cartesianos
Obtener el o los puntos de encuentro de la pelota y el ave