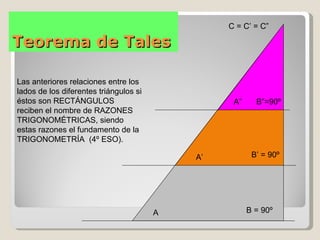
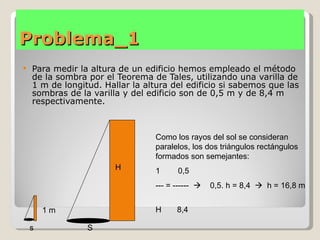
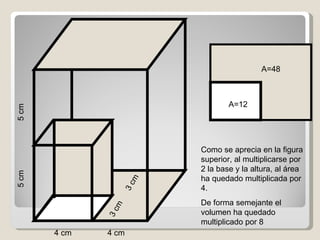
El documento explica el Teorema de Tales, que establece que si dos rectas son cortadas por paralelas, los segmentos resultantes son proporcionales. Como consecuencia, los triángulos formados son semejantes. También describe cómo este teorema se puede usar para medir alturas usando sombras, y presenta tres problemas de aplicación. Finalmente, explica las propiedades de perímetros, áreas y volúmenes bajo semejanza.

1. Teorema de Tales
SEMEJANZA DE TRIÁNGULOS
PERÍMETROS, ÁREAS y VOLÚMENES

2. Teorema de Tales
 Por el Teorema de Tales,
los segmentos resultantes
de cortar a dos rectas por
varias rectas paralelas, son
proporcionales.
 De igual manera los
triángulos que se originan
son semejantes, pues sus
lados son proporcionales y
sus ángulos iguales.
 Los triángulos ROJO, AZUL
y CRIS son semejantes.

3. Teorema de Tales
 Por el Teorema de Tales:
 a b c a+b
a+b+c
a  --- = --- = --- = ----- =
d ---------
 d e f d+e
g
d+e+f
 También, indirectamente:
b  a a+b a+b+c
e  --- = ------ = ---------
 g h i
h  Y también:
 d d+e d+e+f
c  --- = ------ = ---------
f  g h i
i

4. C = C’ = C”
Teorema de Tales
Las anteriores relaciones entre los
lados de los diferentes triángulos
no sería posible si los ángulos de A” B”
lados paralelos no fueran iguales:
A = A’ = A”
B = B’ = B”
A’ B’
A B

5. C = C’ = C”
Teorema de Tales
Las anteriores relaciones entre los
lados de los diferentes triángulos si
éstos son RECTÁNGULOS A” B”=90º
reciben el nombre de RAZONES
TRIGONOMÉTRICAS, siendo
estas razones el fundamento de la
TRIGONOMETRÍA (4º ESO).
A’ B’ = 90º
A B = 90º

6. Problema_1
 Para medir la altura de un edificio hemos empleado el método
de la sombra por el Teorema de Tales, utilizando una varilla de
1 m de longitud. Hallar la altura del edificio si sabemos que las
sombras de la varilla y del edificio son de 0,5 m y de 8,4 m
respectivamente.
Como los rayos del sol se consideran
paralelos, los dos triángulos rectángulos
formados son semejantes:
H 1 0,5
--- = ------  0,5. h = 8,4  h = 16,8 m
1m H 8,4
s S

7. Problema_2
 Para medir la altura de un edificio hemos empleado el método
de la sombra por el Teorema de Tales, utilizando una varilla de
1 m de longitud. Hallar la altura del edificio si sabemos que las
sombras de la varilla y del edificio suman 10 m y la sombra
del edifico, en ese instante, es la cuarta parte de su altura.
Como los rayos del sol se consideran
paralelos, los dos triángulos rectángulos
formados son semejantes:
1 s 1 10 - S
H
--- = ------  ------ = --------
H S 4.S S
1 = 40 – 4.S  4.S = 39  S = 9,75 m
1m
Luego H = 4.S = 4.9,75 = 39 m
s S

8. Problema_3
 Para medir la altura de un edificio hemos empleado el método
de la sombra por el Teorema de Tales, utilizando una varilla de
1 m de longitud. Hallar la altura del edificio si sabemos que la
sombra de la varilla, en ese instante, mide 35,4 m menos que
la altura del edificio; y que la sombra del edificio mide 1,57 m.
Como los rayos del sol se consideran
paralelos, los dos triángulos rectángulos
formados son semejantes:
1 s 1 H – 35,4
H
--- = ------  ------ = ------------
H S H 1,57
1,57 = H2 – 35,4.H  H2 – 35,4.H – 1,57 = 0
1m
Resolviendo la ecuación: H = 35,44 m
s S

9. PROPIEDADES
 Razón de PERÍMETROS, ÁREAS Y VOLÚMENES
 * Razón de los PERÍMETROS = Razón de
semejanza.
 * Razón de las ÁREAS = CUADRADO de la razón
de semejanza.
 * Razón de los VOLÚMENES = CUBO de la razón
de semejanza.

 Escalas.

 ESCALA es la razón de semejanza entre el original y
su representación. ESCALA 1: 200
 Escala gráfica es una recta graduada según la escala
numérica correspondiente.

10. Ejemplo:
 Razón de PERÍMETROS, ÁREAS Y
VOLÚMENES
 Un prisma recto presenta 3 m de largo, 4 m de
ancho y 5 m de alto.
 Se duplica el tamaño de sus dimensiones ( 6 m, 8
m y 10 m respectivamente).
 ¿Cuánto ha aumentado el perímetro de la base?.
 ¿Cuánto ha aumentado el área de la base?.
 ¿Cuánto ha aumentado su volumen?.
 Perímetro antiguo: P = 3+3+4+4 = 14 m
 Perímetro nuevo: P’ = 6+6+8+8 = 28 m
 Vemos que r = 6/3 = 2 es igual que P’ / P =
28/14 = 2

11. … Ejemplo:
 Área base antigua: A = 3.4 = 12 m2
 Área base nueva: A’ = 6.8 = 48 m2
 Vemos que A’/A = 48/12 = 4 es igual que r2 = 22 =
4
 Volumen prisma antiguo: V = 3.4.5 = 60 m3
 Volumen prisma nuevo: V’ = 6.8.10 = 480 m3
 Vemos que V’/V = 480/60 = 8 es igual que r3 = 23 =
8
 En general podemos decir que si en un cuerpo las
dimensiones aumentan (o disminuyen) r veces, las
superficies aumentan (o disminuyen) r2 veces, y los
volúmenes aumentan (o disminuyen) r3 veces.

12. A=48
A=12
5 cm
Como se aprecia en la figura
superior, al multiplicarse por
2 la base y la altura, al área
5 cm
ha quedado multiplicada por
m
3c
4.
De forma semejante el
m
volumen ha quedado
3c
multiplicado por 8
4 cm 4 cm