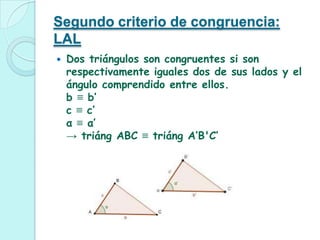
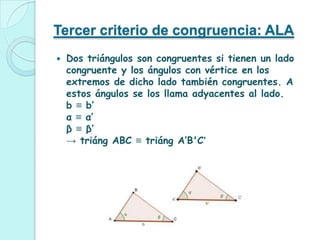
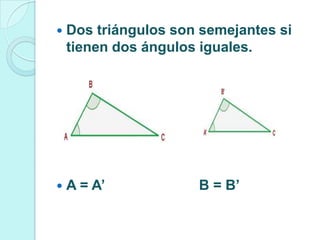
Los criterios de congruencia para triángulos son: 1) tres lados iguales, 2) dos lados y el ángulo entre ellos iguales, 3) un lado y los ángulos adyacentes a ese lado iguales. La congruencia implica que las figuras tienen la misma forma y tamaño aunque su posición sea diferente.

2.  En geometría, dos conjuntos
de puntos son congruentes (o también, están
relacionados por un movimiento) si existe una
isometría que los relaciona: una transformación
que es combinación
de translaciones, rotaciones y reflexiones. Por
así decirlo, dos figuras son congruentes si
tienen la misma forma y tamaño, aunque su
posición u orientación sean distintas. Las partes
coincidentes de las figuras congruentes se
llaman homólogas o correspondientes.

3. Primer criterio de congruencia: LLL
 Dos triángulos son congruentes si sus tres
lados son respectivamente iguales.
a ≡ a’
b ≡ b’
c ≡ c’
→ triáng ABC ≡ triáng A’B'C’

4. Segundo criterio de congruencia:
LAL
 Dos triángulos son congruentes si son
respectivamente iguales dos de sus lados y el
ángulo comprendido entre ellos.
b ≡ b’
c ≡ c’
α ≡ α’
→ triáng ABC ≡ triáng A’B'C’

5. Tercer criterio de congruencia: ALA
 Dos triángulos son congruentes si tienen un lado
congruente y los ángulos con vértice en los
extremos de dicho lado también congruentes. A
estos ángulos se los llama adyacentes al lado.
b ≡ b’
α ≡ α’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’

6.  Dado el triángulo rectángulo de lados a,b y c, se han
construido las figuras que están a sus lados
copiándolo varias veces y colocándolo en diferentes
posiciones.
 Analiza los ángulos que son congruentes en las
distintas posiciones. ¿Podrías deducir que el
cuadrado que se forma es congruente en ambas
figuras?

7.  En la figura, se ha superpuesto un
cuadrado sobre otro
congruente, formando un octógono
regular.
 Demuestra que los triángulos que se
forman son congruentes.

9.  Dos triángulos son semejantes si
tienen dos ángulos iguales.
 A = A’ B = B’

10.  Dos triángulos son semejantes si
tienen los lados proporcionales.
 a/a’=b/b’=c/c’

11.  Dos triángulos son semejantes si
tienen dos lados proporcionales y
el ángulo comprendido entre ellos
igual.
 B=B’ a/a’=c/c’