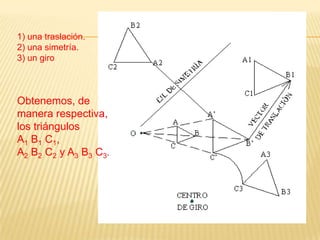
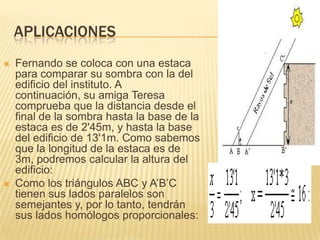
El documento describe cómo transformaciones como homotecias, traslaciones, simetrías y giros aplicadas a un triángulo ABC producen triángulos semejantes. Explica que para que dos triángulos sean semejantes deben tener ángulos iguales y lados correspondientes proporcionales, y provee ejemplos de cómo se puede usar la semejanza para calcular alturas usando sombras.

1. SEMEJANZA
En la figura tienes el resultado de aplicarle al
triángulo ABC las siguientes
transformaciones:
Le aplicamos la homotecia, y al resultado
A’B’C’ lo sometemos a:

2. 1) una traslación.
2) una simetría.
3) un giro
Obtenemos, de
manera respectiva,
los triángulos
A1 B1 C1,
A2 B2 C2 y A3 B3 C3.

3. OBSERVAMOS QUE EN CUALQUIERA DE LOS CASOS, LOS
LADOS CORRESPONDIENTES SON PROPORCIONALES Y LOS
ÁNGULOS NO HAN VARIADO. LA RAZÓN DE
PROPORCIONALIDAD ES LA DE LA HOMOTECIA.
DIREMOS QUE CUALQUIERA DE LOS TRIÁNGULOS
RESULTANTES ES SEMEJANTE AL ABC.
 Diremos que cualquiera de los
triángulos resultantes es
semejante al ABC.

4. EN CONCLUSIÓN…
 La semejanza es la transformación del
plano que resulta de componer un
movimiento y una homotecia.
Llamaremos razón de semejanza a la
razón de la homotecia correspondiente.

5. PROPIEDAD
La semejanza de triángulos equivale a cualquiera de las
siguientes propiedades:
 a) Tienen sus ángulos iguales.
 b) Tienen los lados correspondientes proporcionales.
 c) Tienen un ángulo igual y proporcionales los lados
que lo forman.
 En particular, de a) se deduce que:
 a1) si dos triángulos tienen sus lados paralelos o
perpendiculares, serán semejantes,
 a2) si dos triángulos rectángulos tienen un ángulo agudo
igual, serán semejantes.

6. APLICACIONES
 Fernando se coloca con una estaca
para comparar su sombra con la del
edificio del instituto. A
continuación, su amiga Teresa
comprueba que la distancia desde el
final de la sombra hasta la base de la
estaca es de 2'45m, y hasta la base
del edificio de 13'1m. Como sabemos
que la longitud de la estaca es de
3m, podremos calcular la altura del
edificio:
 Como los triángulos ABC y A’B’C
tienen sus lados paralelos son
semejantes y, por lo tanto, tendrán
sus lados homólogos proporcionales: