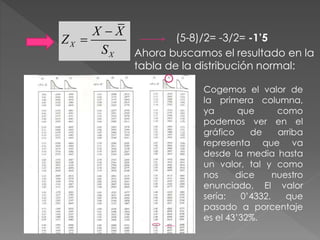
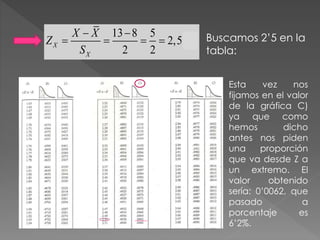
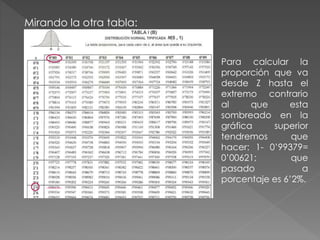
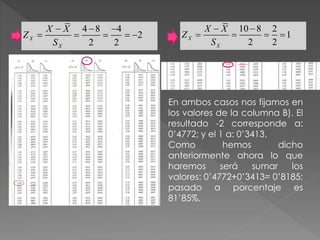
El documento resume los pasos para calcular las proporciones de mujeres destinatarias de asistencia que tienen diferentes puntuaciones en una escala de autoestima de 0 a 13. Se calcula que el 43.32% tienen puntuaciones entre 5-8, el 6.2% tienen puntuaciones mayores o iguales a 13, y el 81.82% tienen puntuaciones entre 4-10.

2. 1. En una muestra de 500 mujeres que reciben
asistencia queremos saber cómo la pobreza
afecta a su autoestima: -media autoestima=8
-deviación típica=2
¿Qué porcentaje de las destinatarias de la
asistencia tienen puntuaciones de autoestima
entre 5 y 8?
Hay que transformar las puntuaciones en
tipificadas (Z), para ello empleamos la siguiente
fórmula:

3. X
X
X X
Z
S

 (5-8)/2= -3/2= -1’5
Ahora buscamos el resultado en la
tabla de la distribución normal:
Cogemos el valor de
la primera columna,
ya que como
podemos ver en el
gráfico de arriba
representa que va
desde la media hasta
un valor, tal y como
nos dice nuestro
enunciado. El valor
sería: 0’4332, que
pasado a porcentaje
es el 43’32%.

4. Si lo miramos en la otra tabla sería:
Como podemos
observar en esta
tabla los valores
representan el
gráfico superior,
es decir, desde
un extremo hasta
Z. Por otro lado,
sabemos que
desde el extremo
a 0(media) está
el 50% de los
datos (0’5).
Por ello, al valor que nos da la tabla (0’93319) le tenemos que restar
0’5. De tal forma que: 0’93319-0’5= 0’43319. Que pasandolo a
porcentaje y redondeando tenemos el mismo resultado que
antes43’32%

5. -Diríamos que un poco más del 43% de las
destinatarias de asistencia están entre 5 y 8 de
autoestima.
-O si una persona se selecciona al azar, hay un
43’32% de posibilidades de que la persona tenga
una autoestima entre 5 y 8.
¿Qué proporción de mujeres destinatarias tiene
una puntuación igual o mayor de 13 en la escala
de autoestima?
En este caso nos preguntan por una proporción
que va de un valor situado por encima de la media
hasta el extremo.

6. 13 8 5
2,5
2 2
X
X
X X
Z DE
S
 
    Buscamos 2’5 en la
tabla:
Esta vez nos
fijamos en el valor
de la gráfica C)
ya que como
hemos dicho
antes nos piden
una proporción
que va desde Z a
un extremo. El
valor obtenido
sería: 0’0062, que
pasado a
porcentaje es
6’2%.

7. Mirando la otra tabla:
Para calcular la
proporción que va
desde Z hasta el
extremo contrario
al que esta
sombreado en la
gráfica superior
tendremos que
hacer: 1- 0’99379=
0’00621; que
pasado a
porcentaje es 6’2%.

8. -Diremos que, solo 62 de 10.000 destinatarios de
asistencia tienen una puntuación mayor de 13 de
autoestima.
-O si una persona selecciona un archivo donde se
alojan los casos al azar, hay menos de un 1% de
oportunidad de que saliera un caso con una
puntuación de mas de 13 de autoestima.
¿Qué proporción de las destinatarias tiene una
proporción entre 4 y 10 en la escala?
Si nos damos cuenta, nos preguntan de un valor
que está por debajo de la media hasta otro que está
por encima. Por lo que lo que haremos será tipificar
de 4 a la media y luego de la media a 10, y
sumaremos los resultados.

9. 4 8 4
2
2 2
X
X
X X
Z DE
S
  
    
10 8 2
1
2 2
X
X
X X
Z DE
S
 
   
En ambos casos nos fijamos en
los valores de la columna B). El
resultado -2 corresponde a:
0’4772; y el 1 a: 0’3413.
Como hemos dicho
anteriormente ahora lo que
haremos será sumar los
valores: 0’4772+0’3413= 0’8185;
pasado a porcentaje es
81’85%.

10. Con la otra tabla:
En este caso
haremos los
siguientes cálculos:
Para el resultado
1 0’84131 - 0’5=
0’34132
Para el resultado
2 0’97725 - 0’5=
0’47725.
Ahora sumamos
ambos resultados
obtenidos: 0’47725
+ 0’34132= 0’8182,
que pasado a
porcentajes es
81’82%.

11. -El 81’82% de las destinatarias de asistencia tienen
una puntuación entre 4 y 10 de autoestima.
-O si seleccionamos un nombre al azar del archivo de
casos hay el 81’82% de probabilidad de que la
persona seleccionada puntúe entre 4 y 10 de
autoestima.