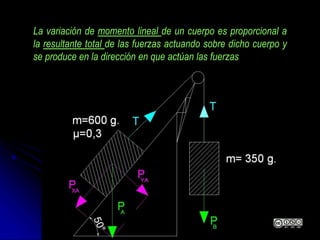
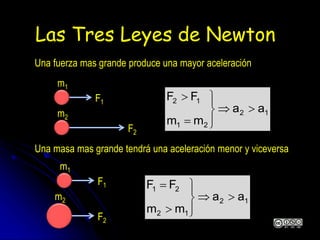
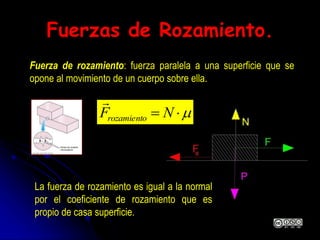
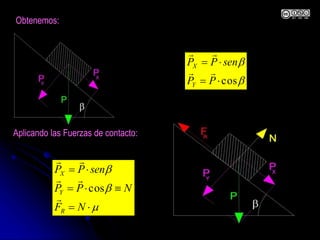
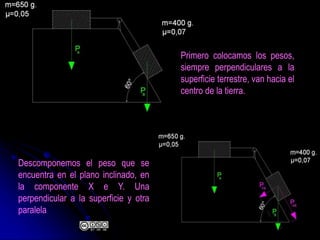
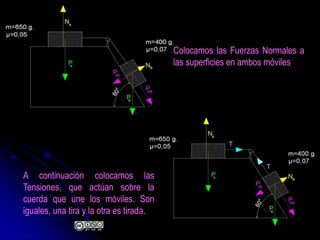
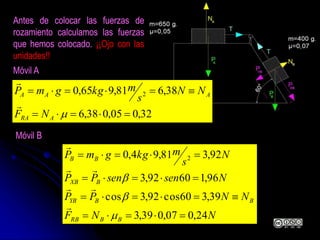
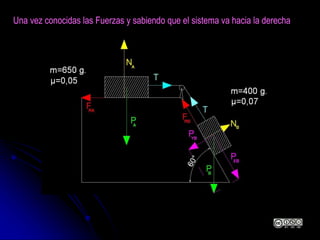
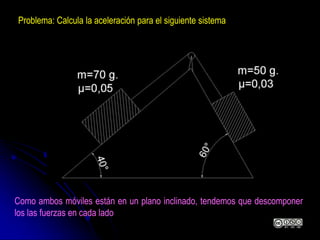
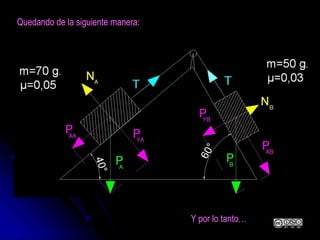
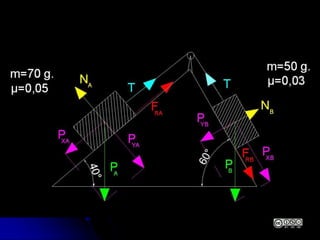
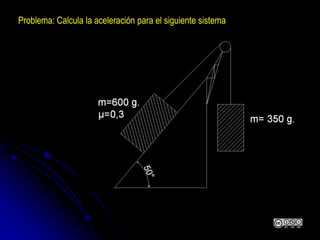
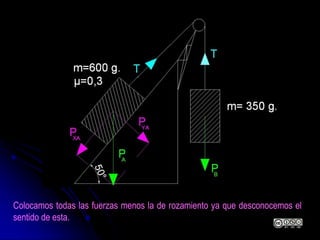
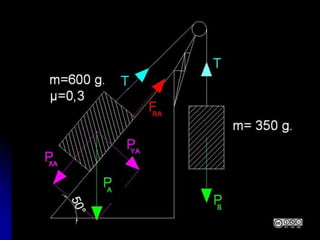
El documento aborda la dinámica en física y química, centrándose en las leyes de Newton y cómo la fuerza, la masa y la aceleración interactúan. Se discute la ley de inercia, la conservación del momento lineal y la acción y reacción entre cuerpos en movimiento. Además, se proporcionan ejemplos prácticos y problemas relacionados con las leyes de dinámica y sus aplicaciones.

1. Tema - Dinámica
Profesor.- Juan Sanmartín
Física y Química
Recursos subvencionados por el…

2. Fenomenología
La dinámica estudia la causa del movimiento.
Hechos observables
 El movimiento de un cuerpo es el resultado de su
interacción con otros.
 La masa inercial de un cuerpo es una propiedad que
determina cómo cambia su velocidad al interaccionar
con otros cuerpos.
 La interacción afecta por igual a los dos cuerpos
(acción-reacción)

3. Isaac Newton
1642 - 1727
Newton es uno de los mas grandes
científicos.
Profesor, Teólogo, Alquimista, Warde of
the Mint, Presidente de la Royal Society,
miembro del Parlamento. Coinventor del
cálculo. Descubridor de la ley de la
Gravitación Universal y de las tres leyes
de Newton del movimiento. Formuló la
teoría Corpuscular de la luz y la ley de
enfriamiento. Hizo la mayor parte de su
trabajo antes de los 25 años.
Visita con los alumnos de 4º a la tumba
de Sir Newton (Abadia Westminster)

4. Ley de Inercia y conservación
del momento lineal







...
0
0321
URMctev
v
FFFFi

Si la fuerza externa resultante que actúa en un objeto es cero,
entonces la velocidad del objeto no cambiará. Un objeto en reposo
permanecerá en reposo; un objeto en movimiento continuará
moviéndose con velocidad constante (M.R.U.). Un cuerpo se acelera
solamente si una fuerza actúa sobre él.

5. El cinturón de seguridad evita que
al frenar o chocar el coche
nuestro cuerpo vaya hacia
delante. Esto ocurre por la Ley de
Inercia, llevamos la velocidad que
posee el coche y al frenar, si no
existe una fuerza que nos
detenga (cinturón) nos vamos
hacia delante
Si no hay una fuerza en contra que nos detenga seguiremos avanzando
con la misma velocidad

6. Si pudiéramos eliminar totalmente la fricción, la aplicación de una fuerza provocaría
un movimiento perpetuo.
En la tierra no ocurre, pero en el espacio no existe rozamiento. La sonda Voyager
(imagen) viaja por el espacio a 17 km /s sin que nadie la detenga. Acaba de salir
del sistema solar. Es el primer objeto fabricado por el hombre que lo logra.
Imagen.- www.nasa.gov

7. Para que un cuerpo cambie la dirección de su
movimiento necesita que se le aplique una
fuerza. Las cadenas de la silla del Tiovivo
impiden que la silla salga despedida y hacen
que siga girando.
La Fuerza Gravitatoria
cambia la dirección de los
planetas provocando que
se muevan en órbitas
Imagen.- www.nasa.gov

8. Ley de la Fuerza y la Masa.
 2
. s
m
Kg
N
m
F
aamF 








Si sobre un cuerpo de masa (m) actúa una fuerza neta (F), el cuerpo
adquiere una aceleración (a) que es directamente proporcional al
módulo de la fuerza e inversamente proporcional a su masa, y tiene la
misma dirección y sentido que de la fuerza.
  amFFi

0

9. La fuerza ejercida es
directamente proporcional a la
masa del cuerpo
Mientras que la aceleración
obtenida es inversamente
proporcional a la masa.
La masa de un camión es
mucho mayor que la masa de
una moto. Por eso, aunque la
fuerza del motor del camión es
también mayor, la aceleración
es mayor en la moto.

10. La variación de momento lineal de un cuerpo es proporcional a
la resultante total de las fuerzas actuando sobre dicho cuerpo y
se produce en la dirección en que actúan las fuerzas

11. 1. Si vemos un objeto acelerándose o frenándose, debemos pensar
que una fuerza está siendo aplicada sobre él.
2. Si vemos un objeto que esta cambiando la dirección de su
movimiento, nuevamente debemos suponer que una fuerza está
siendo aplicada sobre él.
3. Si un cuerpo está en reposo o con velocidad constante, no quiere
decir que no haya fuerzas aplicadas sobre él. Lo que nos dice esta ley
es que la fuerza resultante es cero, esto es todas las fuerzas
aplicadas sobre el cuerpo están equilibradas.

12. Las Tres Leyes de Newton
Una fuerza mas grande produce una mayor aceleración
Una masa mas grande tendrá una aceleración menor y viceversa
12
21
12
aa
mm
FF






F1
m2
m1
F2
12
12
21
aa
mm
FF






F1
m2
m1
F2

13. Ley de acción y reacción
Si un cuerpo A ejerce una
fuerza sobre un cuerpo B,
entonces B ejerce sobre A una
fuerza de igual magnitud y
dirección opuesta. FA + FB = 0
Cuando un cuerpo ejerce una fuerza sobre otro, éste ejerce sobre
el primero una fuerza igual y de sentido opuesto
Las fuerzas siempre se presentan en pares de igual magnitud,
sentido opuesto y están situadas sobre la misma recta.
A
FB
B
FA

14. Cuando queremos dar un salto
hacia arriba, empujamos el suelo
para impulsarnos. La reacción del
suelo es la que nos hace saltar
hacia arriba.
Cuando estamos en una piscina y empujamos a alguien, nosotros también
nos movemos en sentido contrario. Esto se debe a la reacción que la otra
persona hace sobre nosotros, aunque no haga el intento de empujarnos a
nosotros.
El flyboard, es un nuevo
deporte acuático que permite
propulsarse por debajo del
agua y alcanzar hasta 12
metros de altura.
Al expulsar estos agua a presión en un sentido, la persona, debido a la
tercera ley de Newton, experimenta una fuerza en el sentido opuesto.

15. Un barco avanza cuando su hélice empuja agua hacia atrás, es decir, en
sentido contrario.

16. Cuando un cuerpo está apoyado sobre una superficie ejerce una
fuerza sobre ella cuya dirección es perpendicular a la de la
superficie. De acuerdo con la Tercera ley de Newton, la superficie
debe ejercer sobre el cuerpo una fuerza de la misma magnitud y
dirección, pero de sentido contrario. Esta fuerza es la que
denominamos Normal y la representamos con N.
Por este principio, ingenieros
y arquitectos calculan la
resistencia de una placa. La
fuerza de respuesta de la
placa SIEMPRE tiene que
ser mayor a la ejercida sobre
ella para que no ceda.

17. Fuerzas de Contacto
Son de origen electromagnético debidas a
interacciones entre las moléculas de cada objeto
Iñaki Perurena

18. Fuerzas de contacto.
Fuerza Normal : fuerza perpendicular a una superficie que se opone a su
deformación.
Objetos deslizándose sobre superficies

19. Fuerza de rozamiento: fuerza paralela a una superficie que se
opone al movimiento de un cuerpo sobre ella.
Fuerzas de Rozamiento.
La fuerza de rozamiento es igual a la normal
por el coeficiente de rozamiento que es
propio de casa superficie.
 NFrozamiento


20. Problemas
de
Dinámica

21. Problema: Un ciclista pesa, junto con su bicicleta, 75 kg. Y se desplaza con una
velocidad de 28,8 m/s. Si sobre el sistema actúa una fuerza de frenado
(rozamiento) de 15 N, calcula:
a. El tiempo que tardará en parar cuando deje de pedalear
b. El espacio que recorrerá a partir de ese instante
  0iF

El ciclista pedalea con velocidad constante, es decir, según
la Primera Ley de Newton.
Al dejar de pedalear la Fuerza de rozamiento detiene la bicicleta.
22,0
75
15
s
m
m
F
aamFrozamiento 



22. Entonces aplicando las fórmulas de M.R.U.A. (Tema I)
stttavv 144
2,0
8,28
2,08,2800 
Y en el apartado b)
mstatvss 6,20731442,0
2
1
1448,28
2
1 22
00 

23. En estos problemas tenemos uno o más cuerpos situados en un plano que
forma un cierto grado con la horizontal.
Para resolver este tipo de problemas
necesitamos descomponer las fuerzas
y para ello necesitamos unos
conocimientos de TRIGONOMETRÍA
Plano Inclinado

24. Trigonometría - Conceptos
222
opuestocontiguo cch 
Por Pitágoras sabemos
Definimos ahora seno, coseno y tangente del ángulo b :
hipotenusa
cateto
sen
opuesto
b
hipotenusa
catetocontiguo
bcos
contiguo
opuesto
cateto
cateto
tag b

25. En nuestro caso:
ó
Definimos:
bb
bb
coscos 

PP
P
P
senPP
P
P
sen
Y
Y
X
X







26. Obtenemos:

b
b



NF
NPP
senPP
R
Y
X



cos
Aplicando las Fuerzas de contacto:
b
b
cos

PP
senPP
Y
X



27. Problemas Planos
Inclinados

28. Problema: Calcula la aceleración para el siguiente sistema
Tenemos un móvil en un plano
inclinado y otro sobre una
horizontal
Primero vamos a colocar las
fuerzas.

29. Primero colocamos los pesos,
siempre perpendiculares a la
superficie terrestre, van hacia el
centro de la tierra.
Descomponemos el peso que se
encuentra en el plano inclinado, en
la componente X e Y. Una
perpendicular a la superficie y otra
paralela

30. Colocamos las Fuerzas Normales a
las superficies en ambos móviles
A continuación colocamos las
Tensiones, que actúan sobre la
cuerda que une los móviles. Son
iguales, una tira y la otra es tirada.

31. Antes de colocar las fuerzas de
rozamiento calculamos las fuerzas
que hemos colocado. ¡¡Ojo con las
unidades!!
32,005,038,6
38,681,965,0 2


ARA
AAA
NF
NN
s
mkggmP


Móvil A
Móvil B
NNF
NNPP
NsensenPP
N
s
mkggmP
BBRB
BBYB
BXB
BB
24,007,039,3
39,360cos92,3cos
96,16092,3
92,381,94,0 2





b
b





32. Una vez conocidas las Fuerzas y sabiendo que el sistema va hacia la derecha

33. Establecemos el sistema con los dos móviles y sumamos. Las tensiones son
iguales y de sentido contrario, se anulan.
  ammFFP
amFT
amTFP
BARARBXB
ARA
BRBXB






Sustituyendo valores
 
233,1
4,065,0
32,024,096,1
4,065,032,024,096,1
s
ma
a






34. Problema: Calcula la aceleración para el siguiente sistema
Como ambos móviles están en un plano inclinado, tendemos que descomponer
los las fuerzas en cada lado

35. Quedando de la siguiente manera:
Y por lo tanto…

36. NNF
NNPP
NsensenPP
N
s
mkggmP
BBRB
BBYB
BXB
BB
01,003,025,0
25,060cos49,0cos
42,06049,0
49,081,905,0 2





b
b




Obtenemos los siguientes valores
NNF
NNPP
NsensenPP
N
s
mkggmP
AARA
BAYA
AXA
AA
03,005,053,0
53,040cos69,0cos
44,04069,0
69,081,907,0 2





b
b





38. Establecemos el sistema con los dos móviles y sumamos. Las tensiones son
iguales y de sentido contrario, se anulan. PXA >PXB entonces establecemos las
fuerzas de rozamiento que siempre se oponen al movimiento.
  ammFPFP
amFPT
amTFP
BARBXBRAXA
BRBXB
ARAXA






Sustituyendo valores
 
217,0
05,007,0
01,042,003,044,0
05,007,001,042,003,044,0
s
ma
a





La aceleración negativa nos indica que el cuerpo no se mueve.
PERMANECE QUIETO.

39. Problema: Calcula la aceleración para el siguiente sistema

40. Colocamos todas las fuerzas menos la de rozamiento ya que desconocemos el
sentido de esta.

41. N
s
mkggmP
NNF
NNPP
NsensenPP
N
s
mkggmP
BB
AARA
AAYA
AXA
AA
43,381,935,0
14,13,079,3
79,350cos89,5cos
51,45089,5
89,581,96,0
2
2











b
b
Obtenemos los siguientes valores
Es mayor PXA que PB por lo que colocamos la Fuerza de Rozamiento en
sentido contraria a PXA . En B consideramos que no hay rozamiento
porque no hay contacto entre las superficies.

43. Establecemos el sistema con los dos móviles y sumamos. Las tensiones son
iguales y de sentido contrario, se anulan. PXA >PB entonces establecemos la
fuerza de rozamiento que siempre se oponen al movimiento.
  ammPFP
amPT
amTFP
BABRAXA
BB
ARAXA






Sustituyendo valores
 
206,0
35,06,0
43,314,151,4
35,06,043,314,151,4
s
ma
a





La aceleración negativa nos indica que el cuerpo no se mueve.
PERMANECE QUIETO.

44. Fin
Busca enlaces a otras páginas relacionadas con el
tema en…
www.juansanmartin.net