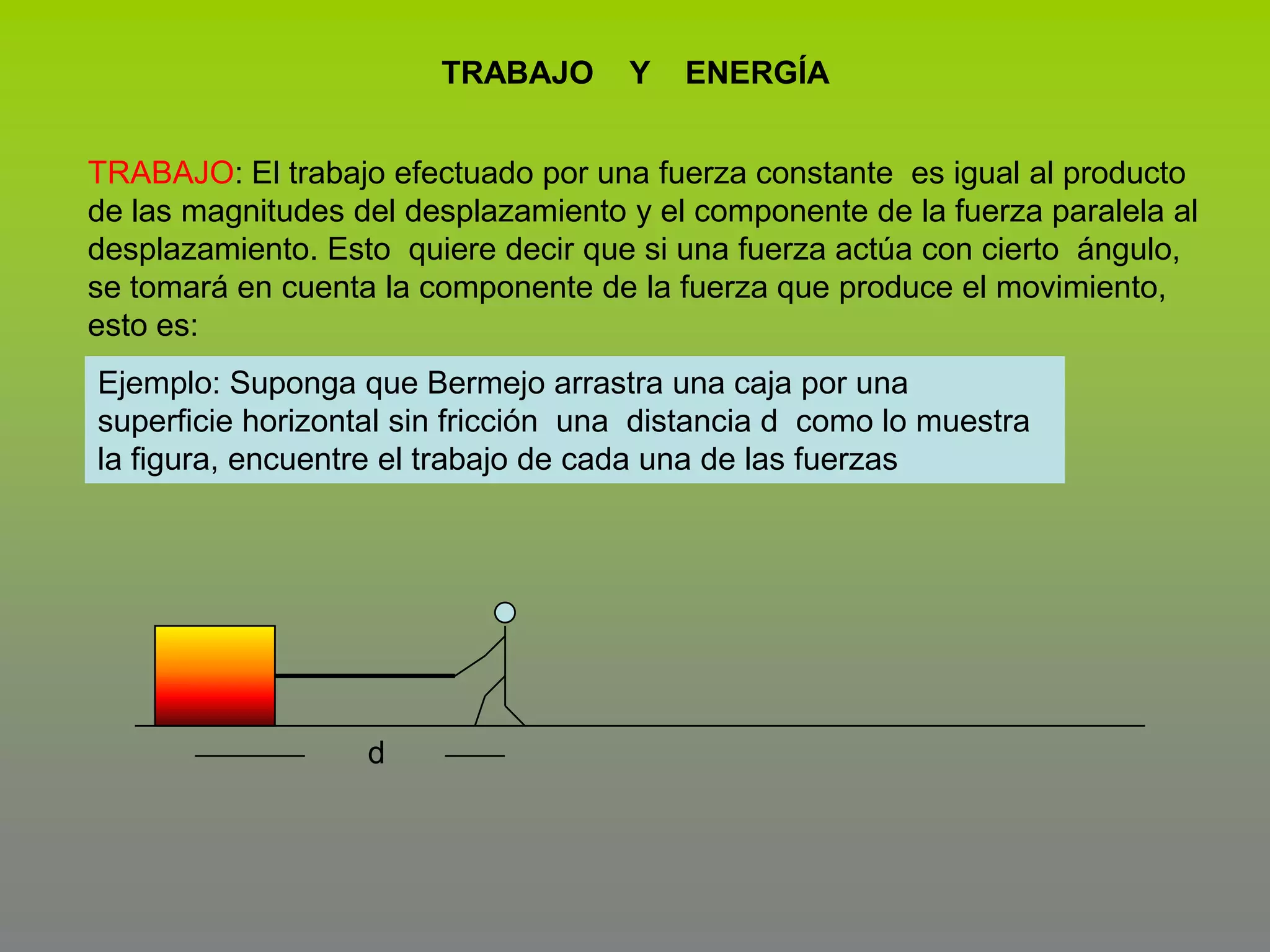
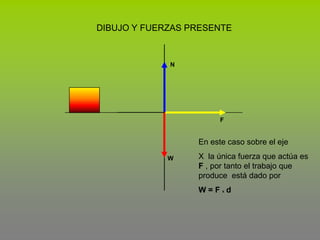
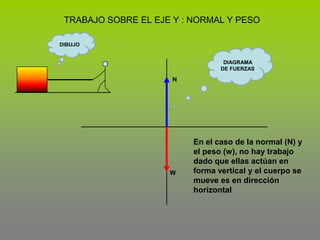
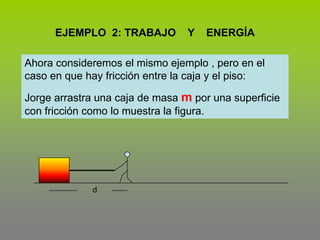
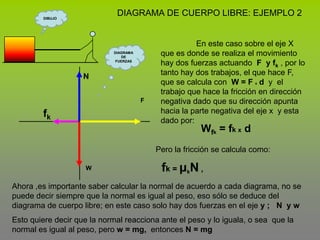
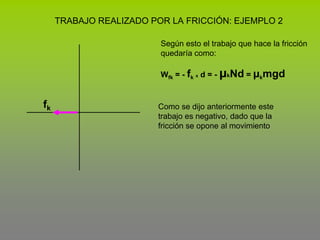
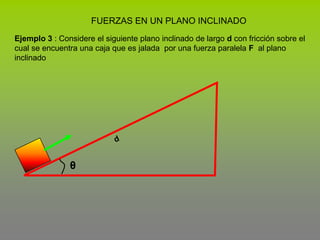
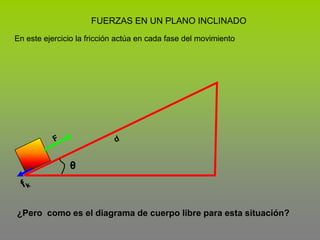
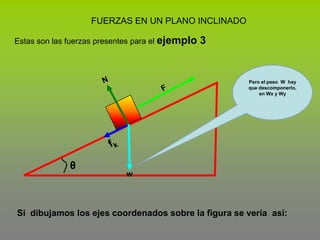
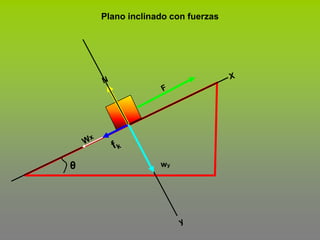
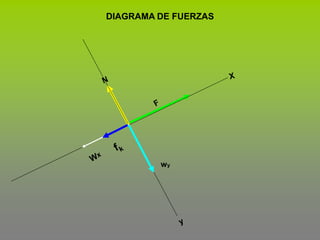
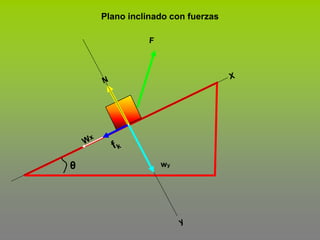
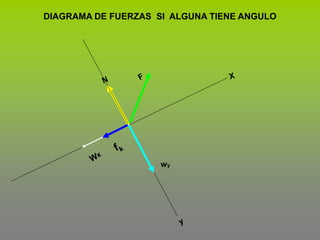
Este documento describe el concepto de trabajo y energía en mecánica. Explica que el trabajo realizado por una fuerza constante es igual al producto de la magnitud de la fuerza por la distancia de desplazamiento en la dirección de la fuerza. Luego presenta tres ejemplos para calcular el trabajo realizado por diferentes fuerzas como la fricción, incluyendo fuerzas en un plano inclinado.

1. TRABAJO Y ENERGÍATRABAJO: El trabajo efectuado por una fuerza constante es igual al producto de las magnitudes del desplazamiento y el componente de la fuerza paralela al desplazamiento. Esto quiere decir que si una fuerza actúa con cierto ángulo, se tomará en cuenta la componente de la fuerza que produce el movimiento, esto es:Ejemplo: Suponga que Bermejo arrastra una caja por una superficie horizontal sin fricción una distancia d como lo muestra la figura, encuentre el trabajo de cada una de las fuerzasd

2. DIBUJO Y FUERZAS PRESENTENFEn este caso sobre el ejeX la única fuerza que actúa es F , por tanto el trabajo que produce está dado por W = F x dW

3. TRABAJO SOBRE EL EJE Y : NORMAL Y PESODIBUJODIAGRAMA DE FUERZASNEn el caso de la normal (N) y el peso (w), no hay trabajo dado que ellas actúan en forma vertical y el cuerpo se mueve es en dirección horizontalW

4. EJEMPLO 2: TRABAJO Y ENERGÍAAhora consideremos el mismo ejemplo , pero en el caso en que hay fricción entre la caja y el piso:Jorge arrastra una caja de masa m por una superficie con fricción como lo muestra la figura.d

5. DIAGRAMA DE CUERPO LIBRE: EJEMPLO 2DIBUJO En este caso sobre el eje X que es donde se realiza el movimiento hay dos fuerzas actuando F y fk , por lo tanto hay dos trabajos, el que hace F, que se calcula con W = F x d y el trabajo que hace la fricción en dirección negativa dado que su dirección apunta hacia la parte negativa del eje x y esta dado por:DIAGRAMA DE FUERZASNFfkWfk = fk x dPero la fricción se calcula como: fk = μkN , WAhora ,es importante saber calcular la normal de acuerdo a cada diagrama, no se puede decir siempre que la normal es igual al peso, eso sólo se deduce del diagrama de cuerpo libre; en este caso solo hay dos fuerzas en el eje y ; N y wEsto quiere decir que la normal reacciona ante el peso y lo iguala, o sea que la normal es igual al peso, pero w = mg, entonces N = mg

6. TRABAJO REALIZADO POR LA FRICCIÓN: EJEMPLO 2Según esto el trabajo que hace la fricción quedaría como:Wfk = - fkx d = - μkNd = μkmgdfkComo se dijo anteriormente este trabajo es negativo, dado que la fricción se opone al movimiento

7. FUERZAS EN UN PLANO INCLINADOEjemplo 3 : Considere el siguiente plano inclinado de largo d con fricción sobre el cual se encuentra una caja que es jalada por una fuerza paralela F al plano inclinadodθ

8. FUERZAS EN UN PLANO INCLINADOEn este ejercicio la fricción actúa en cada fase del movimientodFθfk¿Pero como es el diagrama de cuerpo libre para esta situación?

9. FUERZAS EN UN PLANO INCLINADOEstas son las fuerzas presentes para el ejemplo 3Pero el peso W hay que descomponerlo, en Wx y WyNFfkθwSi dibujamos los ejes coordenados sobre la figura se vería así:

10. Plano inclinado con fuerzas XNFWxfkθwyy

11. DIAGRAMA DE FUERZAS XNFfkWxwyy

12. Plano inclinado con fuerzas FXNWxfkθwyy

13. DIAGRAMA DE FUERZAS SI ALGUNA TIENE ANGULO XFNfkWxwyy