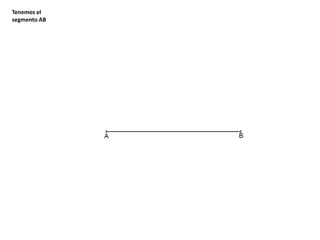
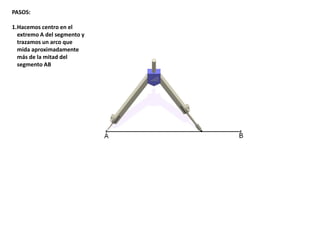
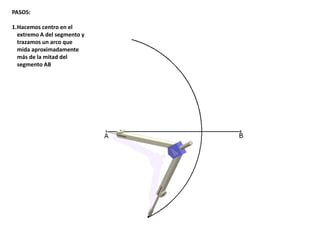
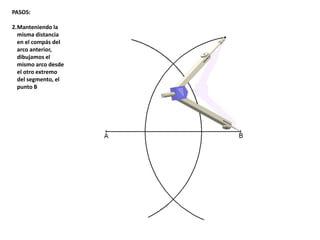
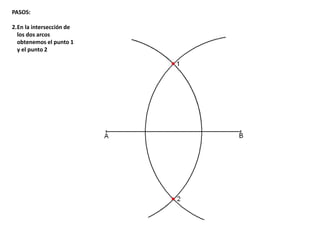
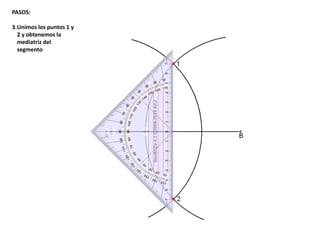
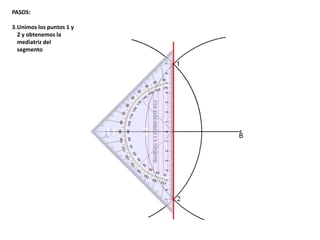
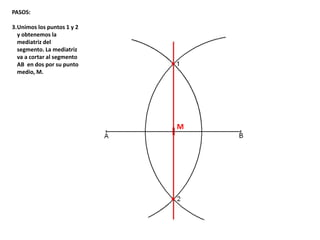
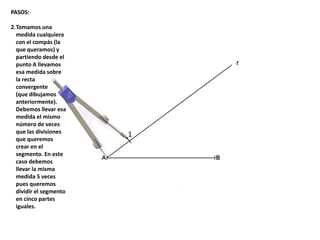
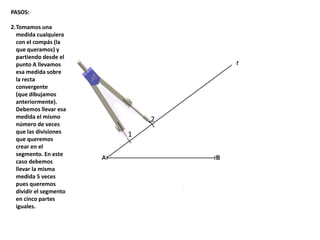
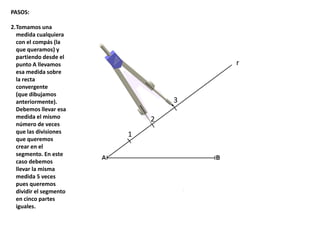
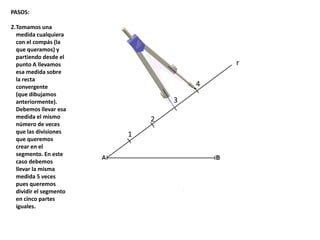
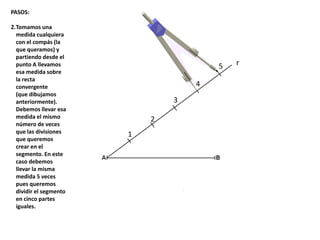
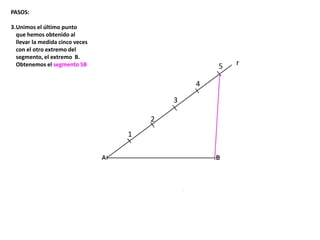
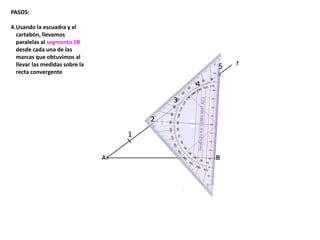
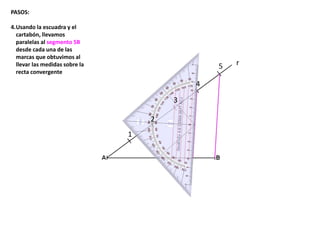
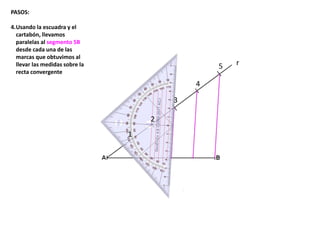
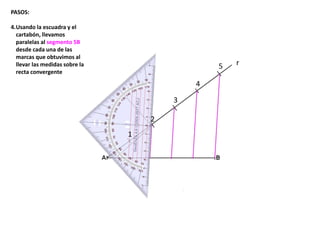
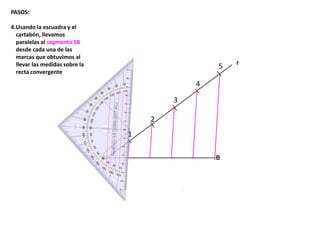
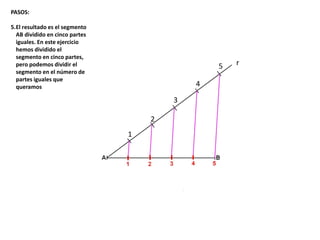
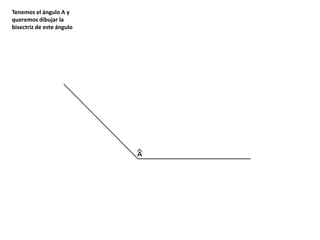
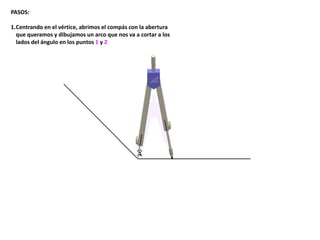
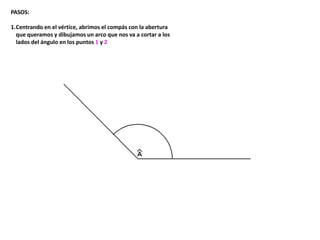
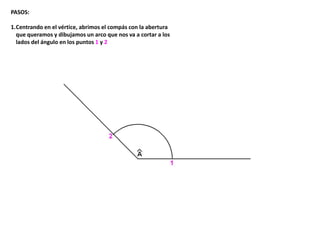
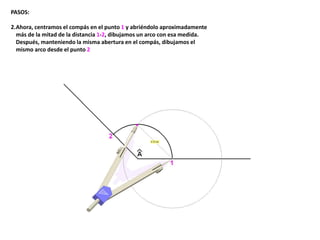
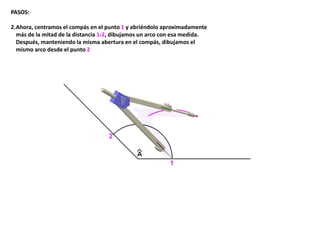
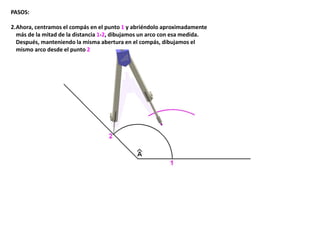
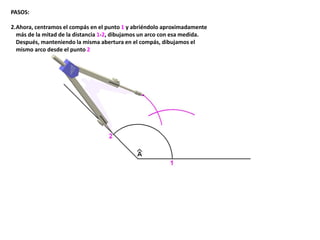
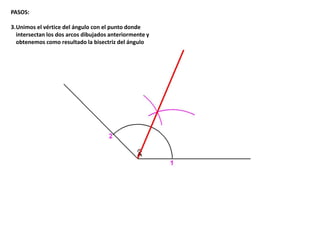
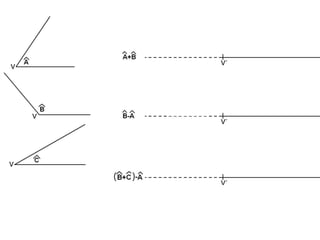
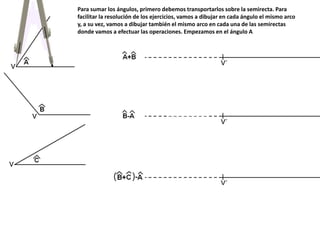
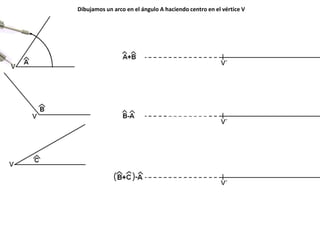
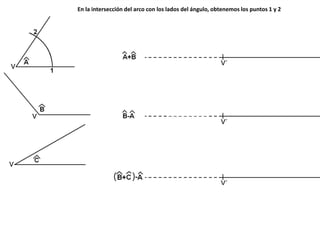
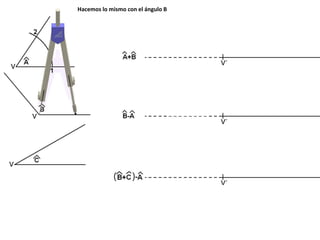
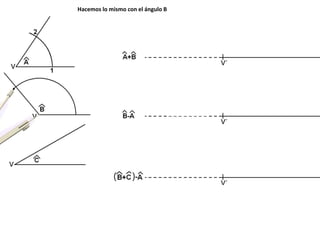
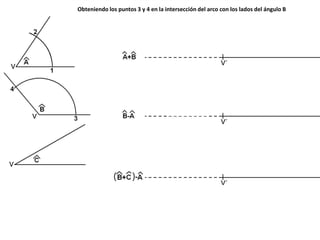
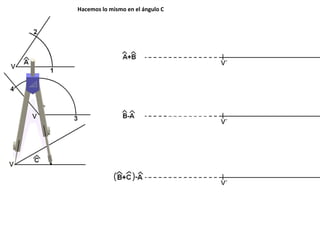
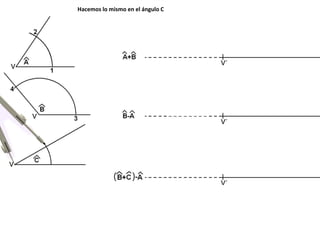
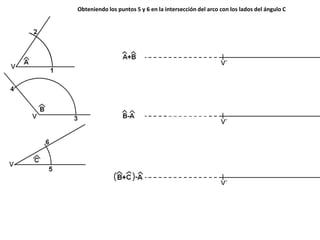
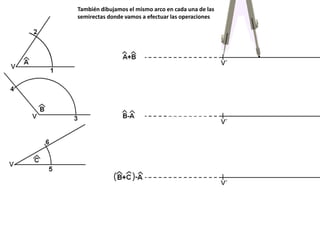
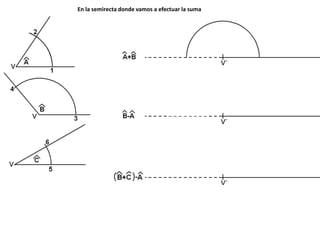
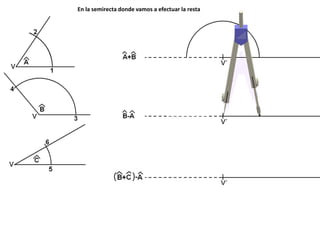
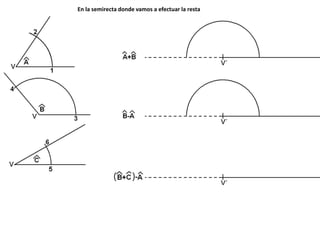
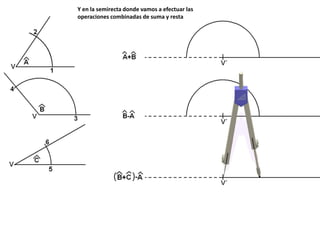
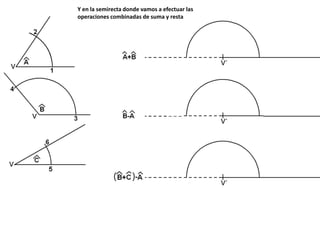
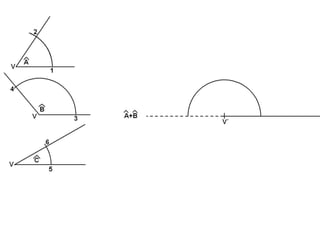
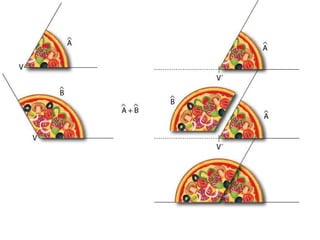
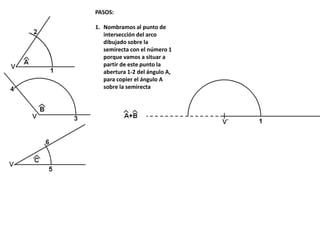
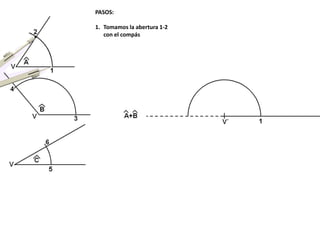
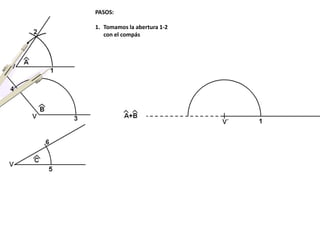
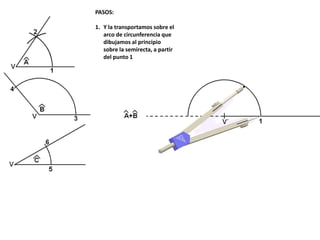
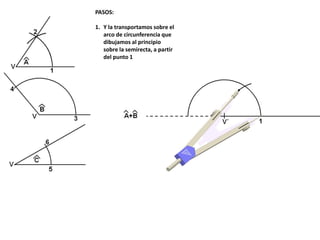
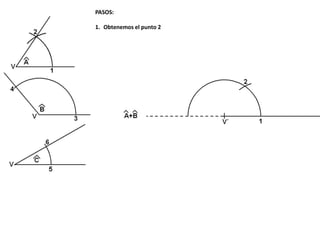
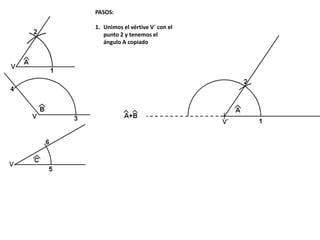
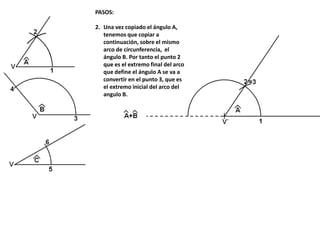
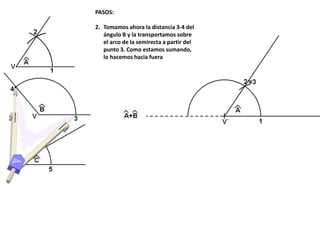
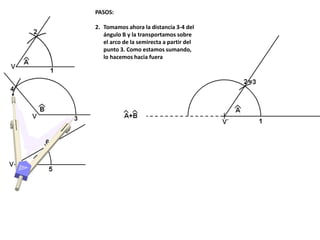
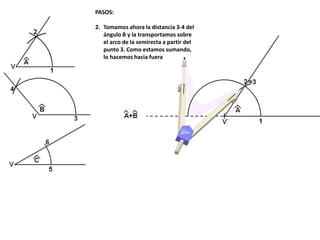
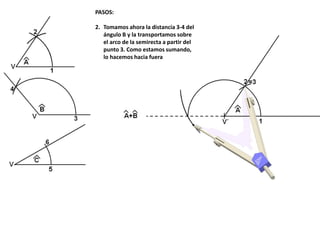
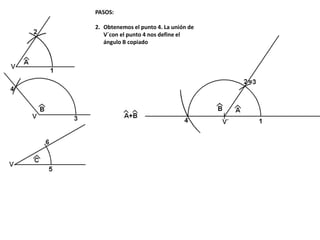
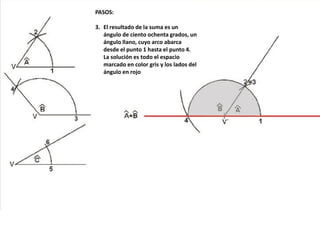
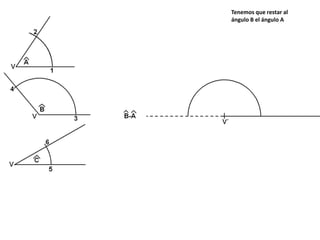
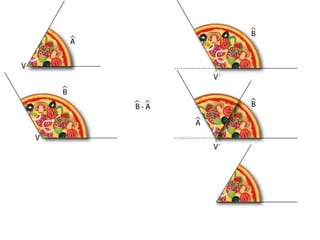
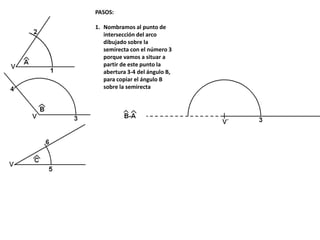
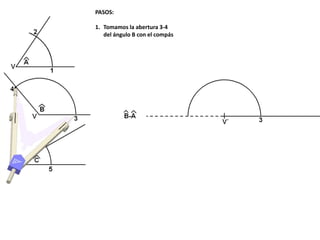
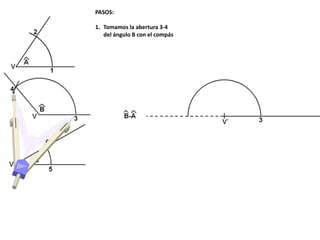
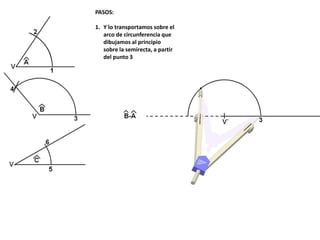
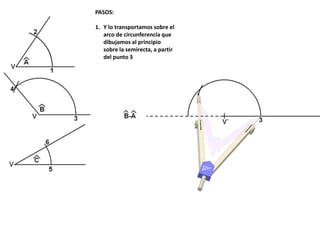
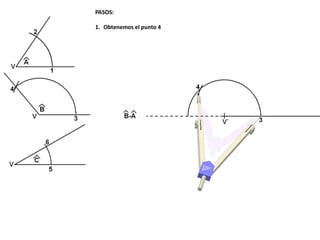
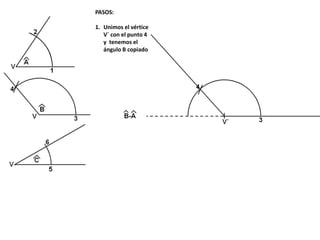
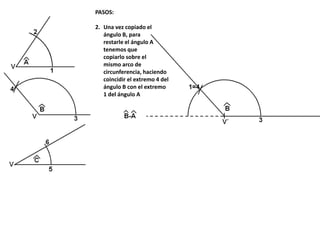
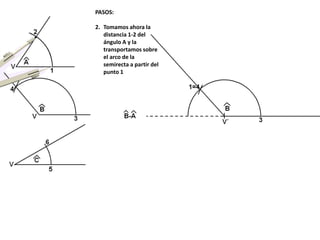
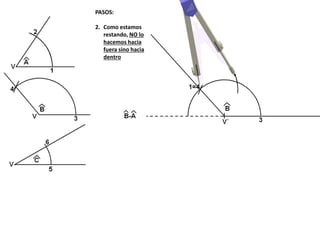
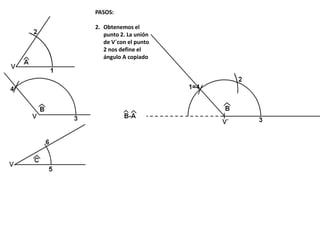
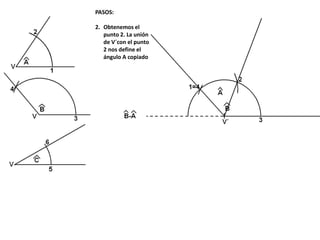
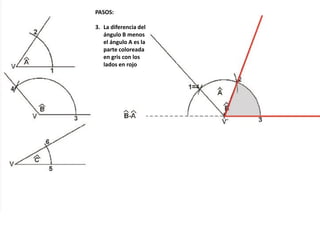
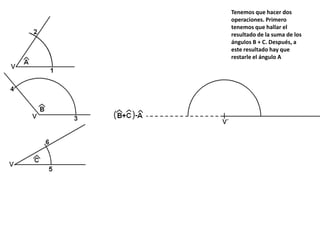
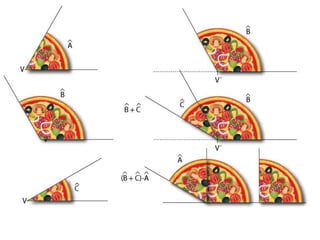
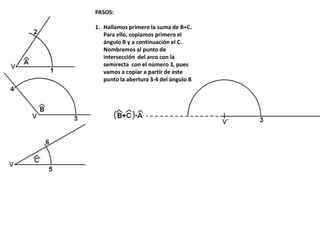
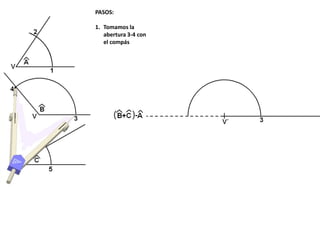
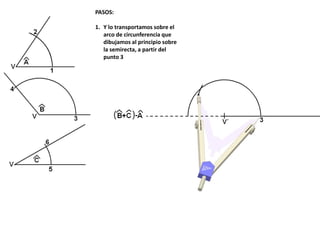
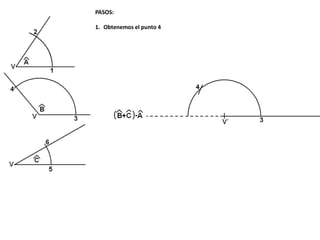
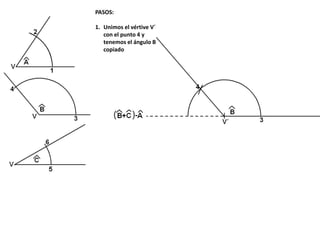
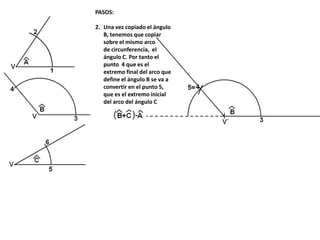
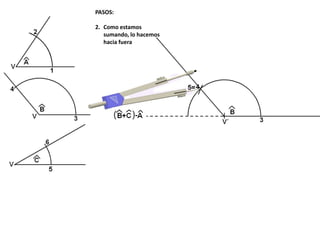
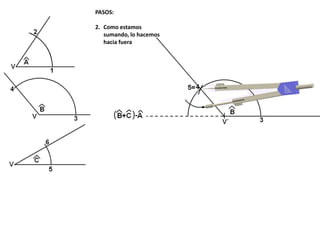
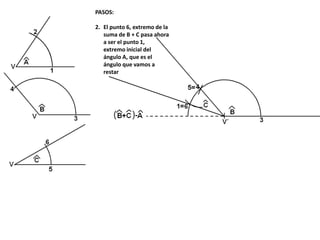
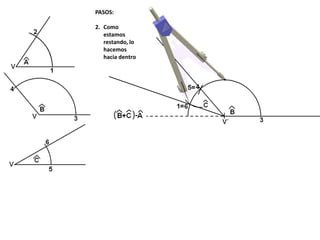
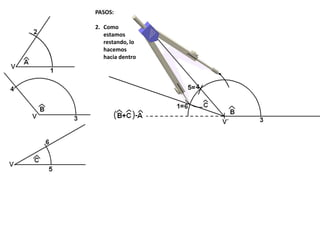
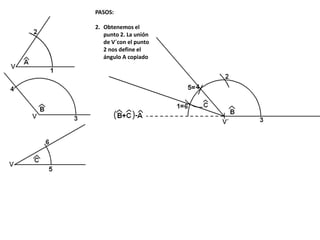
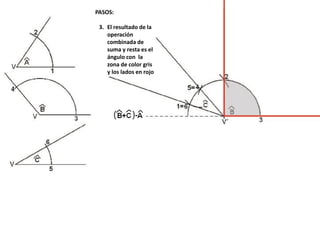
El documento describe los pasos para realizar diferentes operaciones geométricas como trazar la mediatriz de un segmento, dividir un segmento en partes iguales, trazar la bisectriz de un ángulo y sumar ángulos. Explica cómo transportar ángulos sobre una semirecta para facilitar la suma y resta de ángulos.