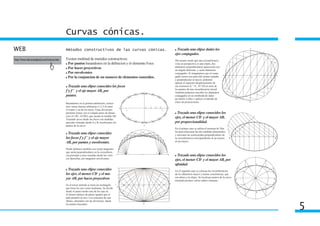
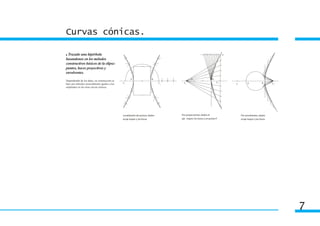
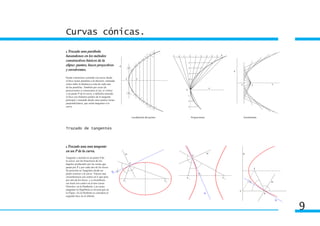
1) El documento describe las características y métodos de construcción de las curvas cónicas, incluyendo elipse, hipérbola y parábola. 2) Explica elementos como focos, ejes, vértices y cómo definir cada curva como el lugar geométrico de puntos que cumplen ciertas propiedades. 3) Detalla métodos para trazar cada curva dado diferentes datos, como focos, ejes o un punto, usando técnicas de puntos, haces o envolventes.

1. Unidad Didáctica 6
Curvas cónicas.

2. Curvas cónicas.
Curvas cónicas.
Elipse.
Hipérbola.
Parábola.
Trazado de las tangentes en un punto de las curvas cónicas.
2

3. Curvas cónicas.
Curvas cónicas Elementos básicos de las curvas cónicas.
Se conoce como curvas cónicas el conjunto de curvas obtenidas al · Focos: Son los puntos de contacto de la sección con las esferas tangentes
seccionar una superficie cónica con un plano; la inclinación de ese al plano que la produce e inscritas en el cono. Están relacionadas con el Tª de
plano con respecto al eje de la superficie cónica determina la curva Dandelin, y la excentricidad, que es la razón de proporción constante, distancia
concreta obtenida. entre un punto de una cónica y el foco , y entre aquel y la recta directriz.
Las curvas cónicas propiamente dichas son tres: Elipse, Parábola e · Diámetros: Rectas que pasan por el centro geométrico. Dos diámetros son
Hipérbola, aunque alterando el cono o la posición del plano pueden conjugados cuando cada uno pasa por la polar del otro. También es el lugar
buscarse otras figuras, entre ellas la circunferencia. geométrico de los puntos medios de todas las cuerdas paralelas al primero.
· Ejes: Mayor y menor. De todos los conjugados los ejes principales son los
únicos que son perpendiculares entre sí.
· Vértice: Cualquier punto del eje mayor sobre la curva.
· Circunferencia focal: De radio igual al eje mayor, y centro en uno de los
focos. En la Parábola el elemento correspondiente es la recta directriz.
· Circunferencia principal o circunscrita: Tiene como diámetro el eje ma-
yor. Una recta tangente a una elipse se corta en ella con las perpendiculares
que se tracen desde los focos.
· Radios vectores: Segmento que une un P de la curva con ambos focos.
3

4. Curvas cónicas.
Elipse. Características, elementos y métodos puede definir como el punto medio del segmento que se traza desde
de construcción. los focos a la circunferencia focal o como el lugar geométrico de los
pies de las perpendiculares trazadas desde los focos a las tangentes .
La elipse es la sección de un cono de revolución con un plano que Esta definición se usará para trazar las tangentes.
corta sólo una de sus ramas y que es oblicuo al eje y a las generatri-
ces. QX=QF1
Características y elementos
Sus elementos cumplen ciertas caracteristicas de tal modo que se la
puede definir tambien por ser el L.G. de los puntos que cumple dichas
caracteristicas.
Tambien podemos definirla como el lugar geométrico de los puntos
1
de un plano en el que se cumple que la suma de los radios vectores es
constante e igual al eje mayor.
F1P + PF2 = d1 + d1 =AB=K= constante
2 Los semiejes de una elipse tambien cumplen una característica que
parte del Tª de Pitagoras.
C
c2 + b2= a2 AB=2a
CD=2b
a
b F1F2=2c
O c
F2
Tambien es lugar geométrico de los centros de las circunferencias
3
tangentes a la circunferencia focal de un foco y que pasa por el otro.
CD= eje menor
4 La circunferencia principal cumple características importantes de AB= eje mayor
C1 circunferencia principal con centro en O de la elipse y de diametro AB, o radio 1/2 AB
relacion entre la focal y la tangente a la elipse. De tal modo que se la C2 circunferencia focal con centro en F1 o F2 y de radio AB
Ctg circunferencia con centro en O de la elipse, tangente a la focal y que pasa por F1 o F2
4

5. Curvas cónicas.
WEB Métodos constructivos de las curvas cónicas. Trazado una elipse dados los
ejes conjugados.
http://www.educacionplastica.net/conicas.htm Existen multitud de metodos constructivos: Del mismo modo que una circunferencia
Por puntos basandonos en la definicion y el elemento Foco. vista en perspectiva es una elipse, dos
Por haces proyectivos diámetros perpendiculares aparecerán con
un ángulo diferente, y serán diámetros
Por envolventes conjugados. Si imaginamos que el conju-
Por la conjuncion de un numero de elementos conocidos. gadel menor era antes del mismo tamaño
y perpendicular al mayor, podemos
aplicar el supuesto desplazamiento de
Trazado una elipse conocidos los focos sus extremos (C’ =C, D’=D) al resto de
los puntos de una circunferencia inicial.
f´y f´´ y el eje mayor AB, por También podemos inscribir los diámetros
puntos. conjugados en un romboide de lados
pa ralelos a ellos y aplicar el método de
Basándonos en la primera definición, coloca- cruce de proyecciones.
mos varias marcas arbitrarias (1,2,3,4) entre
el centro y un de los focos. Estas divisiones
permiten tomar con el compás pares de distan- Trazado una elipse conocidos los
cias (A1/B1, A2/B2), que suman la medida AB.
Trazando arcos desde los focos con medidas
ejes, el menor CD y el mayor AB,
parciales tomadas desde A y B, localizamos los por proporcionalidad.
puntos de la curva.
En el primer caso se utiliza el teorema de Tha-
les para relacionar las dos medidas diametrales,
Trazado una elipse conocidos y trasvasar las semicuerdas perpendiculares de
los focos f´y f´´ y el eje mayor la circunferencia correspondiente al eje menor,
AB, por puntos y envolventes. al eje mayor.
Puede definirse también con rectas tangentes
que serán perpendiculares en la circunferen-
cia principal a otras trazadas desde los vérti- Trazado una elipse conocidos los
ces (derecha), por tangentes envolventes.
ejes, el menor CD y el mayor AB, por
afinidad.
Trazado una elipse conocidos En el segundo caso se colocan las circunferencias
los ejes, el menor CD y el ma- de los diámetros mayor y menor concéntricas, que
yor AB, por haces proyectivos son afines a la elipse. Se localizan puntos de la curva
trazando primero varios radios comunes.
En el tercer método se traza un rectángulo
que tiene los ejes como medianas. Se divide
desde el punto medio uno de los ejes en
el mismo número de partes iguales que el
lado paralelo al otro. Los extremos de este
último, alineados con las divisiones, darán
los puntos buscados.
5

6. Curvas cónicas.
Hipérbola. Características, elementos y mé-
todos de construcción.
La hiperbola es la sección de un cono de revolución con un plano
cuando este es paralelo a dos de sus generatrices.
Características y elementos
r
r´
Sus elementos cumplen ciertas caracteristicas de tal modo que se la
puede definir tambien por ser el L.G. de los puntos que cumple dichas P
cracteristicas. T d1
1 Tambien podemos definirla como el lugar geométrico de los puntos de
d2
un plano en el que se cumple que la diferencia de los radios vectores es F´1
constante e igual a la distancia entre sus vertices del eje real.
2 Los semiejes de una hiperbola también cumplen una característica B
F1 A F2
que parte del Tª de Pitágoras, con una particularidad respecto de la
elipse.
C
a 2 + b2= c 2
AB= 2a
c CD=2b
b
F1F2=2c
O a
c2
3 Tambien es lugar geométrico de los centros de las circunferencias
tangentes a la circunferencia focal de un foco y que pasa por el otro.
4 La circunferencia principal cumple caracteristicas importantes de
relación entre la focal y la tangente a la hipérbola. De tal modo que AB=vertices y eje mayor
se la puede definir como el punto medio del segmento que se traza r y r´= asintotas
c1 circunferencia principal con centro en O y de diametro AB, o radio 1/2 AB
desde los focos a la circunferencia focal o como el lugar geométri- c2 circunferencia focal con centro en F2 y F2 y de diametro 2AB, o radio AB
co de los pies de las perpendiculares trazadas desde los focos a las ctg circunferencia tangente con centro en en P de la hiperbola, tangente a la focal y que pada por F2 o F2
tangentes . Esta definición se usara para trazar las tangentes.
6

7. Curvas cónicas.
Trazado una hipérbola
basandonos en los métodos
constructivos básicos de la elipse:
puntos, haces proyectivos y
envolventes.
Dependiendo de los datos, su construcción se
hace por métodos esencialmente iguales a los
empleados en las otras curvas cónicas.
7

8. Curvas cónicas.
Parabola. Caracteristicas, elementos y
metodos de construccion.
La parábola es la sección de un cono de revolución con un
plano cuando este es paralelo a una de sus generatrices.
F´
Caracteristicas y elementos d1 Q
D P
Sus elementos cumplen ciertas caracteristicas de tal modo
que se la puede definir tambien por ser el L.G. de los puntos
que cumple dichas cracteristicas. d2
1 Tambien podemos definirla como el lugar geométrico de
los puntos de un plano en el que se cumple que equidistan
de una recta llamada directriz y de su foco. V F e
La directriz de la parábola cumple funciones muy simila-
2
res a las de la circunferencia focal en la elipse o hiperbola.
Se la puede considerar una circunferencia focal de centro
D1
impropio ya que la parabola puede ser una elipse de foco
en el infinito, luego su circunferencia focal será de radio Tv
infinito.
3 Tambien es lugar geométrico de los centros de las circun-
ferencias tangentes a la directriz, (focal de radio infinito) y
que pasa por el F.
La tangente en el vértice tiene funciones similares a la
4
circunferencia principal de la elipse o la hipérbola. La
tangente en el vértice es el L.G. de los pies de las perpendi- AB=vertices y eje mayor
r y r´= asintotas
culares trazadas desde el F hasta las tangentes. D1 Directriz (circunferencia focal)
Tv Tangente en el vertice (circunferencia principal)
ctg circunferencia tangente con centro en en P de la parábola,
tangente a la directriz ( c.focal) y que pada por F
8

9. Curvas cónicas.
Trazado una parábola
basandonos en los métodos
constructivos básicos de la
elipse: puntos, haces proyectivos
y envolventes.
Puede construirse cortando con arcos desde
el foco rectas paralelas a la directriz, tomando
como radio la distancia a ésta de cada una
de las paralelas. También por cruce de
proyecciones si conocemos el eje, el vértice
y un punto P de la curva, o definirla uniendo
el foco con distintos puntos de la tangente
principal y trazando desde estos puntos rectas
perpendiculares, que serán tangentes a la
curva.
Trazado de tangentes
Trazado una una tangente
en un P de la curva.
Tangente y normal en un punto P de
la curva: son las bisectrices de los
ángulos producidos por las rectas que
pasan por P y por cada uno de los focos.
Su posición en Tangentes desde un
punto exterior a la curva: Trácese una
circunferencia con centro en E que pase
por uno de los focos, y a circunferen-
cia focal con centro en el otro (recta
Directriz, en la Parábola). Las rectas
tangentes la Hipérbola es inversa que en
la Elipse. En la Parábola se considera el
segundo foco en el infinito.
9