solucionario.

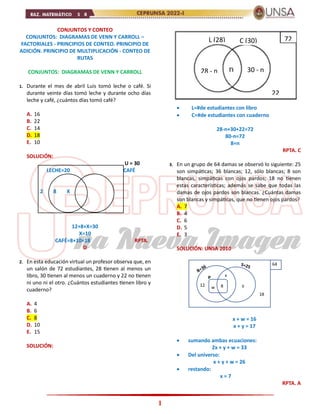
1. 1
CONJUNTOS Y CONTEO
CONJUNTOS: DIAGRAMAS DE VENN Y CARROLL –
FACTORIALES - PRINCIPIOS DE CONTEO. PRINCIPIO DE
ADICIÓN. PRINCIPIO DE MULTIPLICACIÓN - CONTEO DE
RUTAS
CONJUNTOS: DIAGRAMAS DE VENN Y CARROLL
1. Durante el mes de abril Luis tomó leche o café. Si
durante veinte días tomó leche y durante ocho días
leche y café, ¿cuántos días tomó café?
A. 16
B. 22
C. 14
D. 18
E. 10
SOLUCIÓN:
U = 30
LECHE=20 CAFÉ
2 8 X
12+8+X=30
X=10
CAFÉ=8+10=18 RPTA.
D
2. En esta educación virtual un profesor observa que, en
un salón de 72 estudiantes, 28 tienen al menos un
libro, 30 tienen al menos un cuaderno y 22 no tienen
ni uno ni el otro. ¿Cuántos estudiantes tienen libro y
cuaderno?
A. 4
B. 6
C. 8
D. 10
E. 15
SOLUCIÓN:
 L=#de estudiantes con libro
 C=#de estudiantes con cuaderno
28-n+30+22=72
80-n=72
8=n
RPTA. C
3. En un grupo de 64 damas se observó lo siguiente: 25
son simpáticas; 36 blancas; 12, sólo blancas; 8 son
blancas, simpáticas con ojos pardos; 18 no tienen
estas características; además se sabe que todas las
damas de ojos pardos son blancas. ¿Cuántas damas
son blancas y simpáticas, que no tienen ojos pardos?
A. 7
B. 4
C. 6
D. 5
E. 3
SOLUCIÓN: UNSA 2010
x + w = 16
x + y = 17
 sumando ambas ecuaciones:
2x + y + w = 33
 Del universo:
x + y + w = 26
 restando:
x = 7
RPTA. A
L (28) C (30)
22
72
28 - n 30 - n

2. 2
4. Según estadísticas del 2019, treinta millones de
personas visitaron dos de los parques de atracciones
más frecuentados de Disney en Orlando: el Magic
KIngdom y el Disney Hollywood Studios. Se sabe que,
de estos, 9 millones visitaron ambos parques y que el
número de personas que solo visitaron Hollywood
Studios es la novena parte de los que visitaron Magic
Kingdom. ¿Cuántos millones visitaron el parque
dedicado al cine?
A. 10
B. 20
C. 12
D. 16
E. 8
SOLUCIÓN:
𝒙 + 𝟗 +
𝒙 + 𝟗
𝟗
= 𝟑𝟎
𝟗𝒙 + 𝟖𝟏 + 𝒙 + 𝟗 = 𝟐𝟕𝟎
𝟏𝟎𝒙 = 𝟏𝟖𝟎
𝒙 = 𝟏𝟖
 Hollywood Studios fue visitado por: 𝟑𝟎 − 𝟏𝟖 =
𝟏𝟐 millones
RPTA. C
5. Pedro resolvió problemas de Razonamiento
Matemático o Física durante todas las tardes de los
días múltiplos de seis de cada mes del año 2020. Si
resolvió problemas de razonamiento matemático 33
tardes y de física durante 35 tardes, ¿cuántas tardes
resolvió problemas de los dos cursos en el 2020?
A. 7
B. 8
C. 2
D. 9
E. 10
SOLUCIÓN:
 Días de enero: 6, 12, 18, 24, 30
 U=5(12)-1 = 59
33+35 – x = 59
x= 9
RPTA. D
6. El diagrama de Venn muestra información sobre las
mascotas de 40 estudiantes.
 ξ = 40 estudiantes
 C = estudiantes que tienen un gato
 D = estudiantes que tienen un perro
¿Cuál será el cociente de los que no poseen
solamente gato con la diferencia de los que tienen
solamente gato y los que no poseen ni gato ni perro?
A. La raíz cuadrada de un primer compuesto de 2 cif.
B. Ni primo ni impar por tres
C. La diferencia de cifras de un último primo de 2 cif.
D. El producto de divisores de 4
E. Ni primo ni compuesto
SOLUCIÓN:
x(x+3) + 7 + 4x + 3x – 6 = 40
x2
+3x +7 + 4x + 3x – 6 = 40
x2
+ 10x – 39 = 0
 x1 = -13 y x2 = 3
Entonces solamente gato = 18

3. 3
solamente perro = 12
ni perro ni gato = 3
diferencia positiva = 18 – 3 = 15
Cociente = 15/15 = 1 RPTA. E
7. Se hizo una encuesta sobre 3 series al grupo 309-I y se
obtuvo la siguiente información:
- Los estudiantes que ven Naruto y Candy son la
mitad de los que miran Naruto.
- Todos los que ven Naruto, ven Dragonball.
- Los estudiantes que no ven Candy ni Dragonball,
son 10.
- A 60 estudiantes, no les gusta Naruto.
- Los que ven Dragonball o Candy, pero no Naruto,
son 4 veces más que los que ven Naruto.
¿Cuántos estudiantes ven las 3 series?
A. 4
B. 5
C. 8
D. 10
E. 20
SOLUCIÓN:
 A 60 estudiantes, no les gusta Naruto:
𝒂 + 𝒃 + 𝒄 + 𝟏𝟎 = 𝟔𝟎
𝒂 + 𝒃 + 𝒄 = 𝟓𝟎
 Los que ven Dragonball o Candy, pero no
Naruto, son 4 veces más que los que ven
Naruto:
𝟓𝟎 = 𝟓(𝟐𝒙)
𝒙 = 𝟓
RPTA. B
8. De 72 alumnos, 36 estudian en el día, 35 en la tarde y
25 en la noche. ¿Cuántos estudian en solo dos turnos,
si solo uno estudia en tres turnos?
A.21
B. 18
C. 20
D.23
E. 22
SOLUCIÓN:
 x+y+z+a+b+c+1=72
 x+y+z+a+b+c=71

71
:
1 36
1 35
1 25
3 96
93
71 93
22
por conjuntos
x a c
y a b
z b c
x y z a b c a b c
x y z a b c a b c
a b c
a b c
   
   
   
         
        
   
  
RPTA. E
9. De un grupo de personas en una reunión la tercera
parte de las mujeres bailan y la séptima parte de los
hombres están sentados. ¿Cuántas personas no
bailan si se contaron 24 personas en la pista de baile?
A. 26
B. 25
C. 30
D. 27
E. 28
SOLUCIÓN:

4. 4
 Tenemos: 6Q=12
K=12
 NO BAILAN =Q+2K=2+24=26
RPTA. A
10. Freddy como parte de su investigación de tesis sobre
dos antivirus en dos sistemas operativos, obtiene que
el 70% utilizan Windows 10, de ellos el 30% usan el
antivirus NOD32 y el resto utilizan el antivirus AVAST,
mientras los que usan el sistema operativo Mac, de
los cuales la mitad utilizan el NOD32, si se sabe que
224 usuarios utilizan el antivirus AVAST, el total de
encuestados es:
A. 300
B. 250
C. 350
D. 400
E. 320
SOLUCIÓN:
 Construyendo nuestro diagrama de Carroll.
Nod32 Avast
Windows
10
21% 49% 70%
Mac 15% 15% 30%
64% 100%
 Aplicando una regla de tres:
64% ---- 224
100% ---- 𝒙
𝒙 = 𝟑𝟓𝟎
RPTA. C
11. En un Congreso de Internacional de Metalurgia donde
asistieron 336 personas, se observa que las ingenieras
5/8 son solteras. De los ingenieros, se sabe que son
los 2/5 del total de ingenieras y 1/10 del número de
ingenieras casadas están embarazadas. ¿Cuántas
ingenieras casadas están embarazadas?
A. 8
B. 12
C. 9
D. 90
E. 18
SOLUCIÓN:
INGENIEROS INGENIERAS
x Casado
s
2𝑰𝑴/5 Soltero
s
Embarazadas No
embaraz
adas
 Total de asistentes: 336
𝑰𝑴 +
𝟐𝑰𝑴
𝟓
=
𝟕𝑰𝑴
𝟓
= 𝟑𝟑𝟔
𝑰𝑴 = 𝟐𝟒𝟎
 Ingenieras Solteras:
𝟓𝑰𝑴
𝟖
=
𝟓(𝟐𝟒𝟎)
𝟖
= 𝟏𝟓𝟎
 Ingenieras Casadas: 𝟗𝟎
 Ingenieras Casadas embarazas:
𝟏
𝟏𝟎
(𝟗𝟎) = 𝟗
RPTA. C
12. En la escuela profesional de Ing. Ambiental, después
del primer ciclo universitario de un grupo de
estudiantes, se tiene que 30 aprobaron Química
General, y de las 55 mujeres, 10 aprobaron Física
General, pero no Química General. De los varones, 25
aprobaron Química o Física y 15 desaprobaron los
dos cursos. Si 20 varones desaprobaron química,
¿cuántas mujeres desaprobaron los dos cursos?
A. 35
B. 45
C. 55
D. 65
E. 75

5. 5
SOLUCIÓN:
 Del gráfico, el total de mujeres es 55.
 x + 10 + 10 = 55  x = 35
RPTA. A
13. El aula 101-S del turno I cuenta con 60 estudiantes, de
los cuales:
 A 29 les gusta Matemática, pero no tienen 17
años.
 A 10 no les gusta Lenguaje ni Matemática y son
mayores de 20 años.
 De los que no son mayores de 20 años, a 6 no les
gusta ni Lenguaje ni Matemática.
¿Cuántos estudiantes de 17 años gustan de
Matemática, si son la mitad de todos los que gustan
de Lenguaje?
A. 7
B. 4
C. 3
D. 5
E. 6
SOLUCIÓN:
𝒙 + 𝟐𝟗 + 𝟏𝟎 + 𝟔 + 𝟐𝒙 = 𝟔𝟎
𝟑𝒙 = 𝟏𝟓
𝒙 = 𝟓
RPTA. D
14. En un local de votación hay en lista 120 ciudadanos se
sabe que:
- Doce son varones menores de 30 años.
- 36 varones no son iguales o mayores a 30, ni
menores a 40 años
Tantas mujeres tienen menos de 30 años como
hombres tienen más de 29 años, pero menos de 40
años, los hombres son 8 menos que las mujeres.
¿Cuántas mujeres no tienen menos de 30 años?
A. 44
B. 56
C. 64
D. 32
E. 20
SOLUCIÓN:
Menor
es de
30
Igual o
mayores
a 30, pero
menores
a 40
Igual o
mayore
s a 40
años
mujeres X = 20 44 Y = 64
varones 12 X = 20 24 y-4=56
 Y + y – 8 = 120 total 120
Y = 64
RPTA. A
15. Las secciones de 5to. de secundaria del colegio “LIFE”,
están escogiendo los colores que llevara su casaca de
promoción entre los colores Azul, Rojo, Verde y
Negro. El color más votado es el Negro y el menos
votado es el Azul. 13 solo quieren Azul o Rojo, 9
quieren solo Negro o Verde, 12 quieren más dos
colores; 7 quieren solo Rojo-Verdel o Negro-Azul, si al
final se cuenta 16 quieren que se utilice los colores
Rojo - Azul y 13 los colores Verde-Negro; ¿cuántos
estudiantes estaban en la reunión?
A. 35
B. 50
C. 69
D. 30
E. 48
SOLUCIÓN:
M L
x
29
10
6
U=60
2x
20
17
17-20

6. 6
 13 solo quieren Azul o Rojo =>
X+Y=13
 9 quieren solo Negro o Verde => W+Z=9
 12 quieren más 2 colores => M +N+ O+ P + k
=12
 7 quieren solo Rojo-Verdel o Negro-Azul =>
A+C =7
 16 se utilice los colores Rojo – Azul =>
X+B+Y=16
=> B=3
 13 los colores Verde-Negro => W + D
+ Z=16
=> D = 4
 X+Y +W +Z + A+C+D+B+ M +N+ O+ P + k
13 + 9 + 7 + 4 +3 + 12 = 48
RPTA. E
FACTORIALES
16. Una persona tenía “x” años en el año 2000.
Determine la edad que tendrá en el año bicentenario
de nuestra patria, si:
𝟓𝟎𝟒𝟎. (𝟕𝟐𝟎)𝟐𝟒!
= (𝟔!)(𝟒!)!
. (𝟑 + 𝒙)!
A. 25
B. 26
C. 21
D. 27
E. 30
SOLUCIÓN:
𝟓𝟎𝟒𝟎. (𝟕𝟐𝟎)𝟐𝟒!
= (𝟔!)𝟐𝟒!
. (𝟑 + 𝒙)!
𝟓𝟎𝟒𝟎 = (𝟑 + 𝒙)!
𝒙 = 𝟒
 Por tanto, en el 2021 tendrá 25 años.
RPTA. A
17. El número de formas en las que se puede ubicar una
cantidad de personas en una fila de sillas, es a la suma
del número de formas que pueden ubicarse en esta
fila quitando 1 y 2 sillas, como 12 es a 2, ¿cuántas
personas se querían ubicar a un inicio?
A. 7
B. 6
C. 5
D. 4
E. 3
SOLUCIÓN:
𝒏!
(𝒏 − 𝟏)! + (𝒏 − 𝟐)!
=
𝟏𝟐
𝟐
 Entonces: n=7
RPTA. A
18. La edad de Marcos es “x” años, ¿Cuántos años tendrá
dentro de 9 años?
(𝒙 + 𝟏)! (𝒙 − 𝟏)! = 𝟑𝟔𝒙 + (𝒙!)𝟐
A. 10
B. 11
C. 12
D. 13
E. 14
SOLUCIÓN:
(𝒙 + 𝟏)! (𝒙 − 𝟏)! = 𝟑𝟔𝒙 + (𝒙!)𝟐
(𝒙 + 𝟏). 𝒙. (𝒙 − 𝟏)! (𝒙 − 𝟏)! = 𝟑𝟔𝒙 + 𝒙!. 𝒙!
(𝒙 − 𝟏)!𝟐 (𝒙 + 𝟏 − 𝒙) = 𝟑𝟔
(𝒙 − 𝟏)! = 𝟔
𝒙 = 𝟒
4+9=13
RPTA. D
19. María vendedora de juguetes, ofreció un descuento
de “x” soles a uno de sus clientes. Si:
𝟏𝟐𝒙! + 𝟓(𝒙 + 𝟏)! = (𝒙 + 𝟐)!
¿de cuánto fue el descuento?
A. 4
B. 5
C. 6
Azul
Rojo Negro
Verde
X
Y
W
Z
K
B C
A D
M
N
O
P

7. 7
D. 7
E. 1
SOLUCIÓN:
𝟏𝟐𝒙! + 𝟓(𝒙 + 𝟏)𝒙! = (𝒙 + 𝟐)(𝒙 + 𝟏)𝒙!
𝟏𝟐 + 𝟓(𝒙 + 𝟏) = (𝒙 + 𝟐)(𝒙 + 𝟏)
𝒙 = 𝟓
RPTA. B
20. Katherine Julissa fue una estudiante del CEPRUNSA
QUINTOS, quien ingresó a Medicina el año 2019, cuya
edad en ese entonces estaba dada por la suma de
cifras del resultado de:
𝑺 =
𝟏𝟎! − 𝟗!
𝟖!
+
𝟗! − 𝟖!
𝟕!
+ ⋯ + 𝟏!
¿A qué edad ingresó?
A. 17 años
B. 16 años
C. 14 años
D. 15 años
E. 18 años
SOLUCIÓN:
𝑺 =
𝟏𝟎! − 𝟗!
𝟖!
+
𝟗! − 𝟖!
𝟕!
+ ⋯ + 𝟏!
𝑺 =
𝟏𝟎. 𝟗. 𝟖! − 𝟗. 𝟖!
𝟖!
+
𝟗. 𝟖. 𝟕! − 𝟖. 𝟕!
𝟕!
+ ⋯ + 𝟏!
𝑺 = 𝟖𝟏 + 𝟔𝟒 + 𝟒𝟗 + ⋯ + 𝟏
𝑺 = 𝟐𝟖𝟓
𝑬𝒅𝒂𝒅 = 𝑺𝒖𝒎𝒂 = 𝟏𝟓 𝒂ñ𝒐𝒔
RPTA. D
21. Señale el valor entero positivo de "n" que verifica:
(𝒏 + 𝟏)! (𝒏 − 𝟏)! = 𝟑𝟔𝒏 + (𝒏!)𝟐
A. 3
B. 6
C. 4
D. 8
E. 9
SOLUCIÓN:
(𝒏 + 𝟏)! (𝒏 − 𝟏)! = 𝟑𝟔𝒏 + (𝒏!)𝟐
(𝒏 + 𝟏)(𝒏)(𝒏 − 𝟏)! (𝒏 − 𝟏)!
= 𝟑𝟔𝒏 + ((𝒏)(𝒏 − 𝟏)!)𝟐
(𝒏𝟐
+ 𝒏)[(𝒏 − 𝟏)!]𝟐
= 𝟑𝟔𝒏 + 𝒏𝟐[(𝒏 − 𝟏)!]𝟐
𝒏[(𝒏 − 𝟏)!]𝟐
= 𝟑𝟔𝒏
[(𝒏 − 𝟏)!]𝟐
= 𝟑𝟔
(𝒏 − 𝟏)! = 𝟔 = 𝟑!
n = 4
RPTA. C
22. Facto gasta 3𝐴 + 4𝑛 soles para comprar la camiseta
de la selección peruana que usa Lapadula, si:
𝑨 =
𝒏! + (𝒏 + 𝟏)!
𝒏! − (𝒏 − 𝟏)!
=
𝟓!
𝟑𝟐
¿Cuánto cuesta la camiseta de Lapadula?
A. S/ 70
B. S/ 80
C. S/ 75
D. S/ 90
E. S/ 81
SOLUCIÓN:
(𝒏 + 𝟐) ∙ 𝒏!
(𝒏 − 𝟏) ∙ (𝒏 − 𝟏)!
=
𝟏𝟐𝟎
𝟗
(𝒏 + 𝟐) ∙ 𝒏 ∙ (𝒏 − 𝟏)!
(𝒏 − 𝟏) ∙ (𝒏 − 𝟏)!
=
𝟏𝟎 ∙ 𝟏𝟐
𝟗
𝒏 ∙ (𝒏 + 𝟐)
𝒏 − 𝟏
=
𝟏𝟎 ∙ (𝟏𝟎 + 𝟐)
𝟏𝟎 − 𝟏
𝒏 = 𝟏𝟎
 Costo de la camiseta.
𝟑 (
𝟏𝟐𝟎
𝟗
) + 𝟒(𝟏𝟎) = 𝟖𝟎 𝐬𝐨𝐥𝐞𝐬
RPTA. B
23. El número de hermanos que tiene Pedro es “y – x”, si:
 “x” representa el número total de ceros en que
termina 50!
 “y” representa el mayor exponente del único factor
“7” resultante en 100!
¿cuántos hermanos tiene Pedro?
A. 1
B. 2
C. 3
D. 4

8. 8
E. 5
SOLUCIÓN:
 El número de ceros en que termina 50!
 x = # de ceros=10 + 2 = 12
 números múltiplos de 7 menores que 100: 7; 14;
21; 28; 35; 42; 7x7; 56; 63; 70; 77; 84; 91;
7x7x2
 único factor 7 resultante en 100!: 716
=7y
,
entonces y=16
y – x = 16 – 12 = 4
 Pedro tiene 4 hermanos.
RPTA. D
24. Alejandro, formador pedagógico se presentará para la
convocatoria del servicio de tutoría en modalidad
virtual para la ejecución del Programa Formativo con
el objetivo de fortalecer la competencia digital de
docentes y coordinadores pedagógicos de 375
Instituciones Educativas con Jornada Escolar, para
ello, practica su desempeño disciplinar y se propone
a resolver lo siguiente:
(𝒏 + 𝟐)! (𝒏 + 𝟒)!
(𝒏 + 𝟐)! + (𝒏 + 𝟑)!
= 𝟏𝟐𝟎
Hallar el complemento aritmético del valor de” n”
A. 9
B. 5
C. 6
D. 7
E. 8
SOLUCIÓN:
(𝒏 + 𝟐)! (𝒏 + 𝟒)(𝒏 + 𝟑)(𝒏 + 𝟐)!
(𝒏 + 𝟐)! + (𝒏 + 𝟑)(𝒏 + 𝟐)!
= 𝟏𝟐𝟎
(𝒏 + 𝟐)! (𝒏 + 𝟒)(𝒏 + 𝟑)(𝒏 + 𝟐)!
(𝒏 + 𝟐)! [𝟏 + 𝒏 + 𝟑]
= 𝟏𝟐𝟎
(𝒏 + 𝟒)(𝒏 + 𝟑)(𝒏 + 𝟐)!
(𝒏 + 𝟒)
= 𝟏𝟐𝟎
(𝒏 + 𝟑)(𝒏 + 𝟐)! = 𝟏𝟐𝟎
𝒏 = 𝟐
RPTA. E
25. Dadas las siguientes proposiciones sobre factoriales,
dar su valor de verdad.
I. Se puede demostrar que el 0! =1 a partir de su
definición.
II. El factorial de 6,7,8,9 ,10,11, y 12 es divisible por
9.
III. Existe factorial de los enteros negativos
A. VVV
B. FVF
C. VFF
D. FVV
E. VVF
SOLUCIÓN:
(1) Si n!= n (n-1)!→(n-1)!=n!/n
Reemplazando, n=1: (1-1)!=1!/1 =0 (V)
(2) Si l 6!=720 (divisible por 9)
Por propiedad los múltiplos de 720, también serán
divisibles por 9 (V)
(3) No existe factorial de los negativos, porque:
Si n!= n (n-1)! , al reemplazar n=0
0!=0x -1!
No se verifica y por inducción/contradicción
podemos inferir que no tiene solución para
ningún entero negativo. (V)
RPTA. A
26. Pascual dice: “Amor mío, dime cuantos días falta para
que llegue nuestro hijo de Francia”, a lo que ella
contesta: “es el valor de “d” que se muestra en la
siguiente ecuación factorial, joven que estás leyendo,
podrías ayudar a Pascual encontrar la respuesta
correcta?
A. 6
B. 7
C. 8
D. 12
E. 14

9. 9
SOLUCIÓN:
(𝒅 + 𝟖)! (𝒅 + 𝟔)!
(𝒅 + 𝟕)! + (𝒅 + 𝟔)!
= 𝟏𝟒!
(𝒅 + 𝟖)! (𝒅 + 𝟔)!
(𝒅 + 𝟔)! [(𝒅 + 𝟕) + 𝟏]
= 𝟏𝟒!
(𝒅 + 𝟕)! = 𝟏𝟒!
𝒅 = 𝟕
RPTA. B
27. En un nuevo gobierno el IGV será del 10 %, ¿a cuánto
asciende el IGV de “M”?
𝑴 =
𝟏𝟏! − 𝟏𝟎!
𝟗!
+
𝟏𝟎! − 𝟗!
𝟖!
+
𝟗! − 𝟖!
𝟕!
+ ⋯ +
𝟐! − 𝟏!
𝟎!
A. 36
B. 36,5
C. 38
D. 38,5
E. 39,9
SOLUCIÓN:
𝑴 =
𝟏𝟏! − 𝟏𝟎!
𝟗!
+
𝟏𝟎! − 𝟗!
𝟖!
+
𝟗! − 𝟖!
𝟕!
+ ⋯ +
𝟐! − 𝟏!
𝟎!
 Se observa que cada sumando tiene la forma:
(𝒏 + 𝟐)! − (𝒏 + 𝟏)!
𝒏!
=
(𝒏 + 𝟐)(𝒏 + 𝟏)𝒏! − (𝒏 + 𝟏)𝒏!
𝒏!
=
𝒏! [(𝒏 + 𝟐)(𝒏 + 𝟏) − (𝒏 + 𝟏)]
𝒏!
= (𝒏 + 𝟏)[(𝒏 + 𝟐) − 𝟏]
= (𝒏 + 𝟏)𝟐
 Aplicando en S:
𝑴 = 𝟏𝟎𝟐
+ 𝟗𝟐
+ 𝟖𝟐
+ 𝟕𝟐
+ ⋯ + 𝟏𝟐
𝑴 =
𝟏𝟎(𝟏𝟎 + 𝟏)(𝟐(𝟏𝟎) + 𝟏)
𝟔
𝑴 = 𝟑𝟖𝟓
 𝑬𝒍 𝟏𝟎% 𝒆𝒔: 𝟑𝟖, 𝟓
RPTA. D
28. Escrito en la pizarra se tiene:
A+B+C= 𝑨𝑩𝑪
̅̅̅̅̅̅
¿Cuándo se cumple la igualdad?
 Juana dice con cuadrados: 𝑨𝟐
+ 𝑩𝟐
+ 𝑪𝟐
=
𝑨𝑩𝑪
̅̅̅̅̅̅
𝟏𝟐
+ 𝟑𝟐
+ 𝟏𝟏𝟐
= 𝟏𝟑𝟏
̅̅̅̅̅̅
 Rocío dice con cubos : 𝑨𝟑
+ 𝑩𝟑
+ 𝑪𝟑
= 𝑨𝑩𝑪
̅̅̅̅̅̅
𝟏𝟑
+ 𝟓𝟑
+ 𝟑𝟑
= 𝟏𝟓𝟑
Si Juana está errada, pero Rocío no. ¿Cuál sería la
suma de los valores que cumplen la ecuación
factorial?
A. 10
B. 9
C. 30
D. 25
E. 80
SOLUCIÓN:
 Los valores son de A, B y C son una cifra:
A+B+C= 𝑨𝑩𝑪
̅̅̅̅̅̅
1!+4!+5!= 𝑨𝑩𝑪
̅̅̅̅̅̅
1+24+120= 145
RPTA. A
29. ¡Encuentre la factorización prima de 12! y escríbalo
en forma estándar.
I. ¿Cuántos ceros habrá al final de la forma numérica
de 12!?
II. ¿Cuál es el valor más grande que es una potencia
de 2 y es factor de 12!?
III. ¿Cuál es el valor más grande que es una potencia
de 6 que sea un factor de 12! ?
A. Tres, 512, 7776
B. Dos, 1024, 1676
C. Uno, 512, 1775
D. Dos, 1024, 1776
E. Uno, 2048, 1176

10. 10
SOLUCIÓN:
I. Dado que 22
· 52
es un factor de 12! = 210
· 35
· 52
· 7 · 11, 100 es un factor de 12! ¡Entonces, hay dos
ceros al final de la forma numérica de 12!
II. ¡El valor más grande que es una potencia de 2
es un factor de 12! = 210
· 35
· 52 · 7 · 11 es 210
= 1,024
III. Dado que 25
· 35
= (2 · 3) 5
= 65
= 7,776, el valor
más grande que es una potencia de 6 que es un
factor de 12! = 210
· 35
· 52
· 7 · 11 es 7.776.
RPTA. D
PRINCIPIOS DE CONTEO - PRINCIPIO DE ADICIÓN -
PRINCIPIO DE MULTIPLICACIÓN
30. Pamelita se presentará para el Concurso Público
de ingreso a la Carrera Pública Magisterial, ella está
estudiando muy animada y se propone a resolver el
siguiente desafío: ¿cuántos números impares de tres
cifras diferentes pueden formarse con los dígitos 3, 4,
5, 6, 7, 8 y 9?
A. 120
B. 130
C. 125
D. 126
E. 137
SOLUCIÓN:
6 5 4
5. 6. 4 = 120
RPTA. A
31. La casaca de Pedro costó tantos soles como números
de la siguiente forma existen:
𝒂 (
𝒃
𝟑
) (√𝒄 + 𝟒)(𝟐𝒂)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅
¿Cuánto costó la casaca de Pedro?
A. S/ 240
B. S/ 250
C. S/ 400
D. S/ 310
E. S/ 210
SOLUCIÓN:
𝒂 𝒃
𝟑
√𝒄
+ 𝟒
𝟐𝒂
4 10 6
 a = 1; 2, 3,4
 b = 0;3; 6;9;12;15;18;21;24;27
 c = 0;1;4;9;16;25
4x10x6 = 240
RPTA. A
32. Mateo tiene una contraseña que consta de dos letras
seguidas de tres dígitos diferentes o viceversa.
¿Cuántas posibles contraseñas diferentes se podrían
formar?, brindar la suma de cifras compuestas de la
respuesta.
A. 15
B. 16
C. 17
D. 18
E. 19
SOLUCIÓN:
LETRAS DÍGITOS
26 26 10 9 8
𝟔𝟕𝟔 𝒙 𝟕𝟐𝟎 = 𝟒𝟖𝟔𝟕𝟐𝟎
486720 x 2 = 973440
 Suma = 9 + 4 + 4 = 17
RPTA. C
33. ¿Cuántos números de 5 cifras contienen uno o dos
ceros juntos y están formados únicamente de cuatros
y doces?
A. 100
B. 32
C. 15
D. 352
E. 88
SOLUCIÓN:
Número de 5 cifras => 𝑨𝑩𝑪𝑫𝑬
̅̅̅̅̅̅̅̅̅̅

11. 11
 Con un cero, cuatros y doses
El cero puede cuatro lugares los demás solo 2
valores
(𝟐)(𝟐)(𝟐)(𝟐)(𝟏)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=16
(𝟐)(𝟐)(𝟐)(𝟏)(𝟐)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=16
(𝟐)(𝟐)(𝟏)(𝟐)(𝟐)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=16
(𝟐)(𝟏)(𝟐)(𝟐)(𝟐)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=16
Total = 64
 Con dos ceros juntos, cuatros y doses
(𝟐)(𝟐)(𝟐)(𝟏)(𝟏)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=8
(𝟐)(𝟐)(𝟏)(𝟏)(𝟐)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=8
(𝟐)(𝟏)(𝟏)(𝟐)(𝟐)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅=8
Total = 24
Total, de números = 88
RPTA. E
34. Ricardo Pitufo tiene 4 polos y 7 pantalones, todas las
prendas de diferente color. ¿De cuántas maneras
diferentes se podrá vestir, sabiendo que el polo azul y
el pantalón blanco, siempre los usa juntos?
A. 28
B. 19
C. 21
D. 16
E. 18
SOLUCIÓN:
3 x 6 + 1 = 19
RPTA. B
35. La promoción de quinto de secundaria de un colegio
del distrito de Alto Selva Alegre desea viajar al Cusco
a fin de año. Si cuenta con 2 líneas aéreas,5 buses
interprovinciales y un tren. ¿De cuántas formas
pueden realizar ese viaje turístico?
A. 10
B. 8
C. 32
D. 7
E. 11
SOLUCIÓN:
 Aplicando el principio de adición o suma (Si
deciden realizar el viaje por cualquier medio de
transporte ya no pueden hacerlo por otro)
2+5+1=8
RPTA.B
36. Mario compra en la tienda “Entra con dinero” los
siguientes artículos: 2 camisas manga corta y 3 manga
larga, 3 pares de zapatillas, 2 pantalones, 2 celulares
y 4 bermudas. ¿De cuántas maneras se puede vestir
Mario con los artículos comprados?
A. 45
B. 90
C. 180
D. 108
E. 144
SOLUCIÓN:
zapatillas y pantalón o
bermuda
y camisa manga corta
o camisa manga
larga
3 ∙ (2 + 4) ∙ (2 + 3)
𝟑 ∙ 𝟔 ∙ 𝟓 = 𝟗𝟎
 Se puede vestir de 90 formas.
RPTA. B
37. Mirella consulta por Internet en tres tiendas
comerciales para comprar un televisor donde le
ofrecieron 5, 7 y 9 líneas de crédito respectivamente
todas diferentes. Una vez decidida en que tienda va a
comprar, ella se va cambiar de ropa, si tiene 3 pares
de zapatillas, 4 buzos (2 iguales), 6 pares de medias y
6 polos (3 iguales). ¿De cuántas maneras distintas
puede adquirir su TV escogiendo una de las líneas de
crédito? y ¿de cuántas maneras puede vestirse? (Dar
como respuesta la suma de ambas preguntas)
A. 212
B. 230
C. 216
D. 237
E. 453
SOLUCIÓN:
 # Maneras que puede adquirir su TV = 5+7+9 =
21
 Las maneras que se puede vestir serían:
Zap Buzos Medias
Polos
3 × 3 × 6 × 4
= 216
 Por tanto: 216 +21 = 237
RPTA. D

12. 12
38. Rafael ha sido contratado por una empresa muy
importante y debe renovar su guardarropa. Para ello,
compra 2 ternos, 3 camisas, 3 corbatas, 3 pares de
medias y un par de zapatos. Ahora cuenta con 4
ternos (2 iguales), 7 camisas (3 iguales), 6 corbatas (2
iguales), 8 pares de medias (3 pares iguales) y 3 pares
de zapatos, ¿de cuántas maneras diferentes se podrá
vestir?
A. 1080
B. 1350
C. 480
D. 960
E. 900
SOLUCIÓN:
Ahora cuenta con 4 ternos, pero 2 son iguales,
entonces solo habrá 3 ternos diferentes; del mismo
modo, serán 5 camisas diferentes, 5 corbatas
diferentes y 6 pares de medias diferentes.
 Por lo tanto: # de maneras diferentes de vestirse
será:
𝟑𝒙𝟓𝒙5x6x3=1350 RPTA. B
39. Si se eligen entre los hombres y las mujeres ò entre
las mujeres o los hombres ò entre los hombres o
mujeres para formar parejas de baile resultan 45
posibilidades. ¿Cuántos hombres bailarán?
A. 5
B. 6
C. 7
D. 8
E. 9
SOLUCIÓN:
 Sea n = número de hombres y es igual al número
de mujeres pues forman parejas.
 Según el texto tenemos: nxn + n+ n + n + n = 45
 Así tenemos n = 5
RPTA. A
40. Jaime, Edú y Lorenzo van a un snack, donde hay 3
variedades de salchipapa, 3 tipos de bebidas (gaseosa
negra, cerveza blanca y jugo de naranja) y tres tipos
cremas. A Jaime no le gusta la gaseosa ni la cerveza,
Edú no gusta de mayonesa ni de kétchup, A Lorenzo
no le gusta la salchipapa mixta y ningún de tipo de
crema. De cuántas maneras se pueden servir los
colegas. Si se sabe que cada uno pide solo una
salchipapa y una sola bebida.
A. 48
B. 2592
C. 1296
D. 1728
E. 288
SOLUCIÓN:
 Calculamos el número de maneras por
separado.
- Jaime:
Salchipapas (3), cremas (0, 1, 2 o 3), Bebidas (1)
𝟑 ∙ (𝟏 + 𝟑 + 𝟑 + 𝟏) ∙ 𝟏 = 𝟐𝟒.
- Edu:
Salchipapas (3), cremas (0 o 1*), Bebidas (3)
𝟑 ∙ (𝟐) ∙ 𝟑 = 𝟏𝟖.
*no pide kétchup ni mayonesa.
- Lorenzo:
Salchipapas (2), cremas (0), Bebidas (3)
𝟐 ∙ (𝟏) ∙ 𝟑 = 𝟔.
 Total de maneras:
𝟐𝟒 ∙ 𝟏𝟖 ∙ 𝟔 = 𝟐𝟓𝟗𝟐
RPTA. B
41. El padre de Duquito oculta sus dulces favoritos en una
caja fuerte de 5 dígitos, si Duquito recuerda que su
padre usaba los números primos que aparecen en su
DNI 29406371. ¿Cuál es el máximo número de
intentos fallidos que podría tener?
A. 1024
B. 242
C. 1023
D. 243
E. 1
SOLUCIÓN:
- Primero encontraremos los números primos del
DNI 29406371.
- Como 5 dígitos en la contraseña donde se usará
cualquiera de estos 3 números multiplicaremos
esas posibilidades (Principio de Multiplicación)
3x3x3x3x3=243
- Como de las 243 posibilidades 1 es la correcta
existirán 242 combinaciones erradas.
RPTA. B

13. 13
42. Le indican a Mónica que aliste a su hermano para
llevarlo a vacunar contra el COVID19 en la estación de
invierno, para ello tiene para escoger: 2 polos, 3
camisas, 4 pantalones, 3 buzos todos los
mencionados anteriormente de diferentes colores;
tiene 2 pares de guantes de color rojo, 3 pares de
guantes de color Azul y para terminar 5 pares de
medias blancas, cuatro pares de zapatos negros, tres
pares de zapatillas diferentes. ¿De cuantas formas
podrá vestir a Jeremías?
A. 60
B. 72
C. 74
D. 76
E. 78
SOLUCIÓN:
- 3 camisas diferentes = 3
- 4 pantalones diferentes = 4
- 2 pares guantes c/ Rojo o 3 c/ azul = 1 + 1 = 2
- 5 pares de medias blancas = 1
- 4 pares de zapatos negros = 1
- PRIMER RESULTADO: 3 x 4 x 2 x 1 x 1 = 24
- 2 polos diferentes = 2
- 3 buzos diferentes = 3
- 2 pares guantes c/ Rojo o 3 c/ azul = 1 + 1 = 2
- 5 pares de medias blancas = 1
- 3 pares de zapatillas diferentes = 3
- SEGUNDO RESULTADO: 2 x 3 x 2 x 1 x 3 = 36
- TOTAL, SERÍA: 24 + 36 = 60
RPTA. A
43. ¿Cuántos paralelogramos se forman cuando un
conjunto de 5 líneas paralelas se cruza con un
conjunto de 4 líneas paralelas?
Detalles y suposiciones: Todas las líneas paralelas se
extienden indefinidamente.
A. La raíz cuadrada de un primer compuesto x 52
B. El cuadrado de la suma de los 2 últimos
números primos de dos cifras
C. La suma de cifras de un penúltimo número
primo de dos cifras por cuatro
D.
Factorial de la suma de dos primos consecutivos
2!
E. El producto de los números primos consecutivos
de una cifra entre tres
SOLUCIÓN:
SOLUCIÓN 1:
 La imagen es engañosa, todas las líneas paralelas
se extienden indefinidamente.
 Se forma un paralelogramo a partir de cada
conjunto de dos líneas en una dirección con cada dos
líneas en la otra.
 Hay
𝒏 (𝒏−𝟏)
𝟐
pares de líneas en una y
𝒎 (𝒎−𝟏)
𝟐
pares
en la otra dirección (con n y m el número de líneas).
 Esto significa que hay
𝒏𝒎 (𝒏−𝟏)(𝒎−𝟏)
𝟒
paralelogramos.
 Entonces: n = 5 y m = 4, produciendo 60.
SOLUCIÓN 2:
 Este es mucho más sencillo. Hay 𝑪𝟐
𝟓
= 10 formas
de elegir dos líneas paralelas del conjunto de cinco.
 Hay 𝑪𝟐
𝟒
= 6 formas de elegir dos paralelogramos
de un conjunto de cuatro.
 Cualquier paralelogramo está determinado
únicamente por un par de líneas de los cinco y un par
de líneas de los cuatro.
 Por lo tanto, el número de posibles
paralelogramos es:
𝑪𝟐
𝟓
𝑪𝟐
𝟒
= (10) (6) = 60
SOLUCIÓN 3:
 La ecuación para encontrar paralelogramos
cuando hay m líneas que intersecan con n líneas, se
puede calcular como m C2
⋅n C2
donde n Cr
representa
n combinación r, o n elige r.
 O en otra forma, (𝒏
𝒓
) o
𝒏!
(𝒏 − 𝒓)! 𝒙 𝒓!
 Sustituyendo m y n como 5 y 4, obtenemos 60.
RPTA. D

14. 14
44. Continuamos en casa y un postulante no encontró
mejor manera que contar las formas de subir 3 pasos,
encontrará que hay 4 formas de subir 3 pasos.
Imagine que las piernas del postulante son tan largas
que tienen la capacidad de subir 11 pasos a la vez.
También se le permite al postulante solo subir hacia
arriba.
Luego, ¿encuentre la cantidad de formas en que
puede subir 11 pasos?
A. 211
B. 29
C. 35
D. 210
E. 45
SOLUCIÓN:
SOLUCIÓN 1:
 Una persona tiene que subir el nn paso
obligatorio. Pero la persona en el primer n – 1 paso
pisa o no pisa sobre este.
 Por lo tanto, hay 2 posibilidades para cada paso
del n− 1 paso.
 por regla del producto, formas totales = 2n − 1
 Aquí n = 11, por lo tanto, formas totales = 211−1
=
210
= 1024.
SOLUCIÓN 2:
 Aquí, hay 11 pasos.
 Ahora, pisar cualquiera de los primeros 10 pasos
no es obligatorio, pero es obligatorio para el 11°
paso, porque es donde tenemos que subir.
 Entonces, hay 2 opciones para los primeros 10
pasos, pero solo 1 para el 11°
 Por lo tanto, según la regla del producto, el
número de formas de subir el 11ª paso es:
2 ∗ 2 ∗ 2 ∗ 2 ∗ 2 ∗ 2 ∗ 2 ∗ 2 ∗ 2 ∗ 2 ∗ 1 = 210
= 1024.
Generalizando: Para n pasos el número de formas
de subir al enésimo paso es 2n – 1
RPTA.
D
CONTEO DE RUTAS
45. ¿De cuántas maneras se puede llegar del punto A al
punto B?
A. 8400
B. 576
C. 7000
D. 8000
E. 700
SOLUCIÓN:
# 𝒎𝒂𝒏𝒆𝒓𝒂𝒔 =
𝟓!
𝟐!. 𝟑!
𝒙
𝟓!
𝟑!. 𝟐!
𝒙
𝟖!
𝟒!. 𝟒!
# 𝒎𝒂𝒏𝒆𝒓𝒂𝒔 = 𝟕𝟎𝟎𝟎
RPTA. C
46. Jesúa y Rolo desean viajar desde la ciudad A hasta la
ciudad F. Halle las rutas que tienen a su disposición,
sin transitar dos veces por cualquier ciudad de la red
vial que a continuación se muestra:
A. 14
B. 15
C. 13
D. 12
E. 16
SOLUCIÓN:
 Considerando como referencia B:
ABEF-ABDF-ABEDF-ABDEF –ABCDF-ABCDEF

15. 15
 Tomando como referencia A-C:
ACDF-ACDEF-ACDBEF-ACBEF-ACBDF-ACBDEF-ACBEDF
 TOTAL = 13
RPTA. C
47. Señale el número de caminos que existen para llegar
a B, partiendo de A, realizando un recorrido mínimo.
Se indica “n” columnas
A. 𝑛2
B.
𝑛(𝑛+1)
2
C.
𝑛(𝑛−1)
2
D.
(𝑛−1)(𝑛+2)
2
E.
(𝑛+1)(𝑛+2)
2
SOLUCIÓN:
 Para 1 columna:
 Para 2 columnas:
 Para 3 columnas:
 𝑷𝒂𝒓𝒂 "n" columnas <>
(𝒏+𝟏)(𝒏+𝟐)
𝟐
RPTA. E
48. La figura mostrada representa una rejilla hecha de
alambre. Si una hormiguita se desplaza por dicha
rejilla, ¿cuántas maneras diferentes existen para
trasladarse si está en A y desea llegar a B, además solo
puede ir a la derecha y hacia abajo?
A. 12
B. 13
C. 15
D. 16
E. 11
SOLUCIÓN:
 Puede trasladarse de 12 maneras
RPTA. A
49. ¿De cuántas maneras puede ir Shrek hacia la princesa
Fiona (siempre avanzando), sin encontrarse con el
burro?
A. 10
B. 15
C. 20
D. 30
E. 35
𝟑 𝒄𝒂𝒎𝒊𝒏𝒐𝒔 <>
𝟐(𝟑)
𝟐
𝟔 𝒄𝒂𝒎𝒊𝒏𝒐𝒔 <>
𝟑(𝟒)
𝟐
𝟏𝟎 𝒄𝒂𝒎𝒊𝒏𝒐𝒔 <>
𝟒(𝟓)
𝟐
A
B
A
B
1
1 1 1
1
1
1
2
3
4
5
3
6
11
12

16. 16
SOLUCIÓN:
 Eliminamos todos los caminos que pasen por
donde está el burro.
RPTA. B
50. El insecto Aragomantispa lacerata camina de G a T
siempre avanzando, pero no debe pasar por R ni S del
siguiente alambrón.
A. 56
B. 57
C. 58
D. 52
E. 54
SOLUCIÓN:
RPTA. A
51. En la siguiente figura, recorriendo solo por los
segmentos, ¿cuántas rutas diferentes existen para ir
del punto A al punto B siguiendo las direcciones
indicadas?
A. 45
B. 50
C. 95
D. 100
E. 72
SOLUCIÓN:
RPTA. D
52. Sin retroceso, ¿De cuántas maneras se puede ir de “F”
a “G”?
A. 32
B. 25
C. 61
D. 75
E. 67
SOLUCIÓN:
 Aplicando la técnica de los nudos(PASCAL), se
tiene que:

17. 17
RPTA. D
53. Se muestra una estructura construida de metal en la
siguiente figura que está conformada por un sistema
de circunferencias tangentes. Un monito pigmeo está
ubicado en el punto A, se desplaza por la estructura
hasta el punto D. ¿De cuántas formas distintas, sin
repetir los puntos, puede realizar dicho recorrido?
A. 110
B. 136
C. 112
D. 135
E. 208
SOLUCIÓN:
RPTA. B
54. Curiosamente, Daniel dibuja segmentos de recta
formando la figura mostrada abajo. ¿De cuántas
maneras diferentes se puede ir del punto A hacia B,
siguiendo las trayectorias indicadas?
A. 32
B. 33
C. 34
D. 35
E. 36
SOLUCIÓN:
(CEPRUNSA 2021 SOCIALES)
RPTA. A
55. ¿Cuántos caminos hay de A hacia E siempre
avanzando?
A. 17
B. 20
C. 26
D. 25
E. 14

18. 18
SOLUCIÓN:
4x3+2x4+2x3
12+8+6
26
RPTA. C
56. Andrea desea viajar desde la Ciudad A, hasta la ciudad
D. ¿De cuántas maneras diferentes puede realizar el
viaje sin pasar ni regresar por el mismo camino?
A. 48
B. 72
C. 60
D. 20
E. 68
SOLUCIÓN: EXAMEN CEPRUNSA 2018
Primera : A B C D = 4 x 3 x 4 = 48
Segunda : A C D = 4 x 4
= 16
Tercera : A D = 4 = 4
Total = 68
RPTA. E
57. Britany construye una malla uniendo chapas con
alambres, como se muestra en la figura.
¿de cuántas formas diferentes una hormiga puede
trasladarse de la chapa A a la B sin pasar dos veces por
la misma chapa ni alambre?
A. 15
B. 40
C. 36
D. 28
E. 52
SOLUCIÓN: EXAMEN CEPRUNSA II FASE 2020
 Damos valores a las demás chapas
 APB= 3x2=6
 APNB= 3x2x3=18
 AMPB= 2x1x2=4
 AMPNB= 2x1x2x3= 12
 Sumamos=6+18+4+12=40
RPTA. B
58. ¿De cuántas maneras se puede llegar de A hasta B sin
retroceder?
A. 11
B. 14
C. 17
D. 20
E. 35
SOLUCIÓN: PERCY AGRAMONTE
RPTA. B
59. ¿Cuántos caminos de menor longitud hay de A hacia
B, viajando a lo largo de la cuadrícula que se muestra
en la figura? y calcular el número de factores positivos
de 11
22
33
44
55
66

19. 19
A. 7790; 1020 factores
B. 8070: 1020 factores
C. 7970: 850 factores
D. 7770; 610factores
E. 7970; 1020 factores
SOLUCIÓN:
 Si se rellenara el orificio central, habría 16 C8 =
12870 trayectos de A a B. Algunos de estos
trayectos pasan por el orificio central y el resto no.
 Determinamos el número de caminos que pasan
por el orificio central es como dos cuadrículas de 4
x 4 unidas en una esquina común.
 Por lo tanto, el número de caminos que pasan por
el orificio central es (8C4) (8C4) = (70) (70) = 4900.
 Por lo tanto, el número de caminos que no pasan
por el orificio central es 12870 - 4900 = 7970.
 La factorización prima del número es:
11
22
33
44
55
66
= (22
)(33
)(44
)(55
)(66
)
= (22
)(33
)(28
)(55
)(26
)(36
)
= (216
)(39
)(55
)
 Cualquier factor de este número tiene una
factorización prima de 2a
3b
5c
donde:
a está entre 0 y 16,
b está entre 0 y 9 y
c está entre 0 y 5, todo incluido.
 Por lo tanto, hay 17 opciones para a, 10 opciones
para b y 6 opciones para c, para un total de 1020
factores.
RPTA. E
CEPRUNSA NUEVA IMAGEN
EQUIPO DE
RAZONAMIENTO
MATEMÁTICO