Soluciones unidad 8

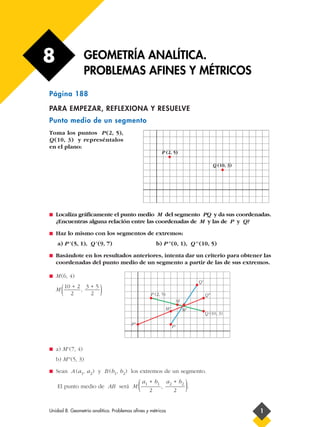
8 GEOMETRÍA ANALÍTICA.
PROBLEMAS AFINES Y MÉTRICOS
Página 188

;;;;;;
PARA EMPEZAR, REFLEXIONA Y RESUELVE
Punto medio de un segmento

;;;;;;
Toma los puntos P (2, 5),
Q (10, 3) y represéntalos
en el plano:

;;;;;;
P (2, 5)

Q (10, 3)

I

I
;;;;;;
Localiza gráficamente el punto medio M del segmento PQ y da sus coordenadas.
¿Encuentras alguna relación entre las coordenadas de M y las de P y Q?

Haz lo mismo con los segmentos de extremos:
a) P' (5, 1), Q' (9, 7) b) P'' (0, 1), Q'' (10, 5)

I Basándote en los resultados anteriores, intenta dar un criterio para obtener las
coordenadas del punto medio de un segmento a partir de las de sus extremos.

I M (6, 4)
Q'
M ( 10 + 2 3 + 5
2
,
2 ) P (2, 5) Q"
M
M" M'
Q (10, 3)

P"
P'

I a) M' (7, 4)
b) M" (5, 3)

I Sean A (a1, a2) y B (b1, b2) los extremos de un segmento.

El punto medio de AB será M ( a1 + b1 a2 + b2
2
,
2
. )
Unidad 8. Geometría analítica. Problemas afines y métricos 1

Ecuaciones de la recta
 x = –3 + 3t
Observa las siguientes ecuaciones: 
y= 2t

I Comprueba que, dando a t los valores 0, 1, 3, 4, 5, se obtienen puntos que es-
tán todos sobre una recta.

 x = 2 + 3t
I Comprueba que las ecuaciones  corresponden también a una recta,
y= 4– t
hallando varios de sus puntos. (Dale a t los valores –2, –1, 0, 1, 2, 3 y repre-
senta los puntos correspondientes; comprobarás que todos están sobre la mis-
ma recta).

I Elimina el parámetro procediendo del siguiente modo:
–– Despeja t en la primera ecuación.
–– Sustituye su valor en la segunda.
–– Reordena los términos de la ecuación resultante.
Obtendrás, así, la ecuación de esa recta, en la forma habitual.

I
t –2 –1 0 1 2 3
(x, y) (–4, 6) (–1, 5) (2, 4) (5, 3) (8, 2) (11, 1)

Y

(–4, 6)
(–1, 5)
(2, 4)
(5, 3)
(8, 2)
(11, 1)
r
X


x–2 
I t=
3  x–2 –x + 14
 → = 4 – y → x – 2 = 12 – 3y → y = →
 3 3
t=4–y
–1 14
→ y= x+
3 3


Distancias en el plano

s
Q (5, 7)

P (3, 2)
r

I Halla la distancia de P y de Q a cada una de las rectas r y s.

I Halla la distancia entre los puntos P y Q (ayúdate del Teorema de Pitágoras).

I Halla, también, la distancia entre:
a) P' (0, 5), Q' (12, 0) b) P'' (3, 1), Q'' (7, 4)

I d (P, r ) = 1; d (P, s ) = 8; d (Q, r ) = 5 = d (Q, s )
— — —
I d (P, Q ) = PQ → PQ 2 = 32 + 42 = 25 → PQ = 5
— — —
I a) d (P', Q' ) = P'Q' → P'Q' 2 = 52 + 122 = 169 → P'Q' = 13
— — —
b) d (P", Q" ) = P"Q" → P"Q" 2 + 42 + 32 = 25 → P"Q" = 5

I d (A, B ) = √ (b1 – a1)2 + (b2 – a2)2 , donde A (a1, a2) y B (b1, b2).
→
d (A, B ) = AB

Página 191
→ →
1. Halla las coordenadas de MN y NM, siendo M (7, –5) y N (–2, –11).
→
MN = (–2, –11) – (7, –5) = (–9, –6)
→
NM = (7, –5) – (–2, –11) = (9, 6)

2. Averigua si están alineados los puntos P (7, 11), Q (4, –3) y R (10, 25).
→ 
PQ = (–3, –14)  –3 –14
→  → = → A, B y C están alineados.
QR = (6, 28)  6 28



3. Calcula el valor de k para que los puntos de coordenadas A (1, 7), B (–3, 4),
C (k, 5) estén alineados.
→ 
AB = (–4, –3)  –4 –3 –5
→  → k + 3 = 1 → –4 = –3k – 9 → 3k = –5 → k = 3
BC = (k + 3, 1) 


Página 192
4. Dados los puntos P (3, 9) y Q (8, –1):
a) Halla el punto medio de PQ.
b) Halla el simétrico de P respecto de Q.
c) Halla el simétrico de Q respecto de P.
— —
d) Obtén un punto A de PQ tal que PA/AQ = 2/3.
— —
e) Obtén un punto B de PQ tal que PB/PQ = 1/5.

a) M ( 3 + 8 , 9 + 2( –1) ) = ( 11 , 4)
2 2


b) 3 + x  P (3, 9)
—––––– = 8 → x = 13
2 
 → P' (13, –11) Q (8, 1)
9+y 
—––––– = –1 → y = –11
2  P' (x, y)


c) Llamamos Q' (x', y') al simétrico de Q respecto de P.

Así: x' + 8  Q'
—––––– = 3 → x' = –2
2 
 Q' (–2, 19) P
y' + (–1) 
—–––––––– = 9 → y' = 19
2  Q


d) Llamamos A(x, y) al punto que buscamos. Debe cumplirse que:
→ 2 → 2
PA = AQ → (x – 3, y – 9) = (8 – x, –1 – y)
3 3


2 
x – 3 = — (8 – x) → x = 5 
3
 A (5, 5)
2 
y – 9 = — (–1 – y) → y = 5 
3


e) Llamamos B(x, y) al punto que buscamos.
→ 1 → 1
PB = PQ → (x – 3, y – 9) = (5, –10) = (1, –2)
5 5
x–3=1 → x=4 
 B (4, 7)
y – 9 = –2 → y = 7 


1. Escribe las ecuaciones paramétricas de las rectas:
→
a) Que pasa por A (–3, 7) y tiene una dirección paralela al vector d (4, –7).
→
b) Que pasa por M (5, 2) y es paralela a d '(2, 2).
En ambos casos, dando valores al parámetro, obtén otros cinco puntos de la
recta.
→ → →
a) OX = OA + t d → (x, y) = (a1, a2) + t (d1, d2) →
 x = a1 + td1  x = – 3 + 4t
→  → 
 y = a2 + td2  y = 7 – 7t

t –2 –1 0 1 2 3
(x, y) (–11, 21) (–7, 14) (–3, 7) (1, 0) (5, –7) (9, –14)

→ → →
b) OX = OM + t d' → (x, y) = (m1, m2) + t (d '1, d '2) →
 x = m1 + td '1  x = 5 + 2t
→  → 
 y = m2 + td '2  y = 2 + 2t

t –2 –1 0 1 2 3
(x, y) (1, –2) (3, 0) (5, 2) (7, 4) (9, 6) (11, 8)

2. Escribe las ecuaciones paramétricas de la recta que pasa por:
a) P (5, –2) y Q (0, 4) b) M (3, 7) y N (3, 0)
c) A (0, 0) y B (7, 0) d) R (1, 1) y S (3, 3)
→  x = 5 – 5t
a) El vector dirección es: PQ = (–5, 6) → 
 y = –2 + 6t
→ → x=3
b) d = MN = (0, –7) → 
 y = 7 – 7t
→ →  x = 7t
c) d = AB = (7, 0) → 
y=0
→ →  x = 1 + 2t
d) d = RS = (2, 2) → 
 y = 1 + 2t

 x = 1 + 3t
3. Halla k para que S (–5, k) pertenezca a r : 
 y = 2 – 4t
 –5 = 1 + 3t → t = –6/3 = –2 
  → k = 2 – 4(–2) = 10
 k = 2 – 4t 


1. Halla el ángulo que forman las siguientes rectas:
 x = 3 – 2t  x = 1 – 4t
r 1:  r 2: 
y=7+t  y = 4 + 3t
→ →
Los vectores directores de r1 y r2 son, respectivamente, d1 (–2, 1) y d2 (–4, 3).
→ →
d1 · d2 8+3 11 11 √ 5
cos α = → → = — — = = ≈ 0,984 → α = 10° 18' 17,4"
d  d 
1 2
√ 5 · √ 25 5 √5 25

2. Obtén para las rectas del ejercicio anterior:
a) La paralela a r 1 que pase por el punto (5, 7).
b) Una perpendicular a r 2 que pase por (0, 0).

→ →
a) r // r1  d = d1  → r :  x = 5 – 2t
 →  
P (5, 7) ∈r  P ∈r  y=7+t
→ → →
b) r' ⊥ r2 → d' ⊥ d2 → d' = (3, 4)  → r ' :  x = 3t
 
P (0, 0)   y = 4t

Página 196
1. Considera las siguientes rectas:

 x = 7 + 5t x=2+t  x = 5 + 3t  x = 5 – 2t
r 1:  r 2:  r 3:  r 4: 
 y = –2 – 3t  y = 1 – 2t  y = –5 – 6t  y = –12 + 4t
Halla la posición relativa de r 1 y r 2, r 2 y r 3, r 3 y r 4.

• Posición relativa de r1 y r2
7 + 5t = 2 + s  5t – s = –5 
  Por 2 la 1- ecuación y se suman:
ª
–2 – 3t = 1 – 2s  –3t + 2s = 3 
10t – 2s = –10
–3t + 2s = 3
7t = –7 → t = –1 → de la 1- ecuación: s = 5 + 5(–1) = 0
ª
Como tiene solución única, entonces r1 y r2 se cortan en el punto P (2, 1) (que
se obtiene sustituyendo t = –1 en r1 o s = 0 en r2).

2 + s = 5 + 3t  s – 3t = 3 
  Las dos ecuaciones son equivalentes.
1 – 2s = –5 – 6t  –2s + 6t = –6 
Luego el sistema tiene infinitas soluciones. Por tanto, r2 = r3 (son la misma recta).


5 + 3t = 5 – 2s  3t + 2s = 0 
  → No tienen solución.
–5 – 6t = –12 + 4s  –6t – 4s = –7 
Luego no tienen ningún punto en común. Por tanto, son paralelas.
Es decir, r3 // r4 .

Página 197
1. Halla las ecuaciones paramétricas de la recta que tiene por ecuación:

5x – 3y + 8 = 0
x=t
Sea x = t → 5t – 3y + 8 = 0 → 
 y = 8/3 + (5/3) t
NOTA – 2-
º MÉTODO

El vector (5, –3) es perpendicular a r. Por tanto, el vector (3, 5) es paralelo a r. Po-
demos tomarlo como vector dirección:
→
d = (3, 5)

Si x = 0 → y =
8
3
. Luego 0, ( )
8
3
∈r

Así, las ecuaciones paramétricas son:
 x = 3t
r: 
 y = 8/3 + 5t
(equivalente a la obtenida por el otro método).

 x = 5 – 3t
2. Halla la ecuación implícita de la recta: 
 y = –1 + 2t
Multiplicamos la primera ecuación por 2 y la segunda por 3, y las sumamos:

2x = 10 – 6t
3y = –3 + 6t
2x + 3y = 7 → r : 2x + 3y – 7 = 0

x–5 
NOTA – 2-
º MÉTODO: x = 5 – 3t → t = 
–3  x–5 y+1
 =
y+1 –3 2
y = –1 + 2t → t = 
2 

2x – 10 = –3y – 3
r : 2x + 3y – 7 = 0


1. Escribe la ecuación de la recta de pendiente 3 y cuya ordenada en el origen es –5.

m=3 
 → r : y = –5 + 3(x – 0) →
P (0, –5) ∈r 
→ r : y = 3x – 5 → ECUACIÓN EXPLÍCITA

→ r : 3x – y – 5 = 0 → ECUACIÓN IMPLÍCITA

2. Halla las ecuaciones de las rectas que pasan por los siguientes pares de puntos:
a) (–7, 11), (1, 7) b) (3, –2), (1, 4)
c) (6, 1), (11, 1) d) (–2, 5), (–2, 8)

y1 – y0 7 – 11 –4 –1  –1
a) m = = = =  y–7= (x – 1)
x1 – x0 1 – (–7) 8 2  2
Tomando el punto (1, 7)  x + 2y – 15 = 0

4+2 6 
b) m = = = –3  y – 4 = –3 (x – 1)
1–3 –2 
Tomando el punto (1, 4)  3x + y – 7 = 0

1–1 
c) m = =0 
11 – 6  y–1=0 → y=1
Tomando el punto (6, 1) 

8–5
d) m = ¡Imposible! Entonces, no tiene pendiente.
–2 + 2
No se puede poner de forma explícita. Es la recta x = –2, paralela al eje Y.

3. Halla dos puntos de la recta y = –3x + 4. Calcula a partir de ellos su pendiente,
y comprueba que es la que corresponde a esa ecuación.
Si x = 0 → y = 4 → A (0, 4) ∈r
Si x = 1 → y = 1 → B (1, 1) ∈r
1–4 –3

;;;
m= = = –3
1–0 1
Efectivamente, es la de la recta y = –3x + 4.

;;;
4. s r Escribe las ecuaciones de las rectas representadas.

;;;
t

 m = –1/2 –1
s:  s → Como s : y = mx + n → s : y = x+3
 Ps (0, 3) 2


 m = 2/3 2 m =0
r:  s → r: y = x + 2; t :  t → t: y = 1
 Pr (0, 2) 3  Pt (0, 1)

Página 201
1. Averigua la posición relativa de los siguientes pares de rectas:

 –x + 3y + 4 = 0  5x + y + 3 = 0
a)  b) 
 3x – 9y – 12 = 0  x – 2y + 16 = 0
Se puede resolver el sistema o bien observar los coeficientes y el término indepen-
diente de ambas ecuaciones:

A –1 3 B 4 C
a) = = = = =
A' 3 –9 B' –12 C'
A B C
Es decir: = = → Son la misma recta.
A' B' C'

5 1 A B
b) ≠ → ≠ → Las rectas se cortan en un punto.
1 –2 A' B'
Para calcular el punto de corte, bastará con resolver el sistema.
Despejando en la primera ecuación: y = –3 – 5x
Sustituyendo en la segunda ecuación:
x – 2(–3 – 5x) + 16 = 0 → x + 6 + 10x + 16 = 0 → 11x = –22 → x = –2
Con lo que:
y = –3 – 5 (–2) = 7 → (x, y) = (–2, 7) → Punto de corte

2. ¿Cuál es la posición relativa de estos dos pares de rectas?
 3x + 5y – 8 = 0  2x + y – 4 = 0
a)  b) 
 6x + 10y + 4 = 0  x–y =0

3 5 –8 A B C
a) = ≠ → = ≠ → Son paralelas.
6 10 4 A' B' C'

b) 2x + y – 4 = 0  2x + x – 4 = 0  3x = 4 → x = 4/3
 
x–y =0 x = y  y = 4/3

Son dos rectas que se cortan en el punto (4/3, 4/3)

Página 202
1. Obtén la distancia entre los siguientes pares de puntos:
a) (3, –5), (1, 4) b) (0, 7), (–5, 7) c) (–2, 5), (–3, –7) d) (8, 14), (3, 2)
→
a) dist (P, Q) = PQ = √ (1 – 3)2 + (4 + 5)2 = √ 4 + 81 = √ 85


→
b) dist (P, Q) = PQ = √ (–5 – 0)2 + (7 – 7)2 = √ 25 + 0 = 5
→
c) dist (P, Q) = PQ = √ (–3 + 2)2 + (–7 – 5)2 = √ 145
→
d) dist (P, Q) = PQ = √ (3 – 8)2 + (2 – 14)2 = √ 169 = 13

2. Halla la distancia de Q (–3, 4) a las siguientes rectas:
x–1 y–4  x = 1 – 2t x y
a) 2x + 3y = 4 b) = c)  d) + = 1
2 5  y = 3 – 6t 2 3

a) 2x + 3y – 4 = 0

2 · (–3) + 3 · 4 – 4 –6 + 12 – 4 2 √ 13
dist (Q, r ) = = = ≈ 0,55
√ 22 + 32 √ 13 13

x–1 y–4
b) = → 5x – 5 = 2y – 8 → 5x – 2y + 3 = 0
2 5
5 · (–3) – 2 · 4 + 3 –15 – 8 + 3 20 √ 29
dist (Q, r ) = = = ≈ 3,71
√ 52 + (–2)2 √ 29 29

x–1 
c) t = 
–2 x–1 y–3
→ –6x + 6 = –2y + 6 → 6x – 2y = 0 → 3x – y = 0

 =
y–3  –2 –6
t= 
–6

3 · (–3) – 4 –9 – 4 13 13 √ 10
dist (Q, r ) = = = = ≈ 4,11
√9 + 1 √ 10 √ 10 10

d) 3x + 2y = 6 → 3x + 2y – 6 = 0

3 · (–3) + 2 · 4 – 6 –9 + 8 – 6 7 √ 13
dist (Q, r ) = = = ≈ 1,94
√ 32 + 22 √ 13 13

Página 207

EJERCICIOS Y PROBLEMAS PROPUESTOS
PARA PRACTICAR
Ecuaciones de la recta
1 Escribe las ecuaciones paramétricas de la recta que pasa por A (–3, 7) y
→
tiene una dirección paralela al vector d (4, –1). Dando valores al parámetro,
obtén otros cinco puntos de la recta.

 x = –3 + 4t t –2 –1 1 2 3

y= 7– t (x, y) (–11, 9) (–7, 8) (1, 6) (5, 5) (9, 4)


2 Escribe las ecuaciones paramétricas de la recta que pasa por:
a) P (6, –2) y Q (0, 5) b) M (3, 2) y N (3, 6) c) A (0, 0) y Q (8, 0)
Halla, en todos los casos, la ecuación implícita.
→  x = 6 – 6t  x = –6t
a) PQ = (–6, 7) → r:  ≡ r:  →
 y = –2 + 7t  y = 5 + 7t
(Usando el punto P ) (Usando Q )

x
→ t= 

–6  x y–5
y–5  → =
t=  –6 7
7 

→ 7x = –6y + 30 → r : 7x + 6y – 30 = 0
→ x=3
b) MN = (0, 4) → r :   x = 3 → recta paralela al eje Y
 y = 2 + 4t
→  x = 8t
c) AQ = (8, 0) → r :  → r : y = 0 → eje X
y=0

3 Halla las ecuaciones paramétricas de cada una de las siguientes rectas:
a) 2x – y = 0 b) x – 7 = 0 c) 3y – 6 = 0 d) x + 3y = 0

x=t
a) Si x = t → 2t – y = 0 → y = 2t → r : 
 y = 2t
x=7 x=t  x = –3t
b)  c)  d) 
y=t  y = 6/3 = 2 y=t

4 Escribe las ecuaciones paramétricas e implícitas de los ejes de coordenadas.
☛ Ambos ejes pasan por el origen de coordenadas y sus vectores directores son los
vectores de la base.

 O (0, 0) ∈ eje X x=t
Eje X :  → → Eje X :  → y=0
 dX = (1, 0) y=0

 O (0, 0) ∈ eje Y x=0
Eje Y :  → → Eje Y :  → x=0
 dY = (0, 1) y=t

5 Halla la ecuación de la paralela a 2x – 3y = 0 cuya ordenada en el origen es –2.
☛ La recta pasa por el punto (0, –2 ).
r : 2x – 3y = 0
s // r → pendiente de s ha de ser igual a la de r 

P (0, –2) ∈s 
 m = mr = 2/3 2
→  s → y= x–2 → 2x – 3y – 6 = 0
 P (0, –2) ∈s 3
ECUACIÓN EXPLÍCITA ECUACIÓN IMPLÍCITA


6 Dada la recta 4x + 3y – 6 = 0, escribe la ecuación de la recta perpendicular a
ella en el punto de corte con el eje de ordenadas.
☛ El eje de ordenadas es el vertical: x = 0.
• Veamos primero cuál es el punto de corte, P (x, y), de la recta con el eje de or-
denadas.
 4x + 3y – 6 = 0
r:  → 4 – 0 + 3y – 6 = 0 → 3y = 6 → y = 2
 Eje Y : x = 0
Luego P (0, 2) ∈r y también debe ser P (0, 2) ∈s, donde s ⊥ r.

• Como s ⊥ r → sus pendientes deben cumplir:
–1 –1 3
ms · mr = –1 → ms = = =
mr –4/3 4
3 3
• Como P (0, 2) ∈s y ms = → y = x + 2 → 3x – 4y + 8 = 0
4 4

7 Escribe las ecuaciones paramétricas de las siguientes rectas:
→ →
a) Su vector de posición es a (–3, 1) y su vector de dirección v (2, 0).
x=1–t
b) Pasa por A (5, –2) y es paralela a: 
 y = 2t
c) Pasa por A (1, 3) y es perpendicular a la recta de ecuación 2x – 3y + 6 = 0.
d) Es perpendicular al segmento PQ en su punto medio, siendo P (0, 4) y
Q (–6, 0), en su punto medio.

a) La ecuación vectorial será:
→ → →  x = –3 + 2t
OX = a + t v → (x, y) = (–3, 1) + t (2, 0) → 
y=1
b) El vector dirección de la recta buscada debe ser el mismo (o proporcional) al de
x=1–t
la recta  (pues debe ser paralela a ella).
 y = 2t
→
Luego: d (–1, 2)
x=5–t
Como debe pasar por A(5, –2) → 
 y = –2 + 2t

c) La pendiente de la recta r : 2x – 3y + 6 = 0 es:
2 –3
mr = → ms = (pues mr · ms = –1 por ser r ⊥ s)
3 2
Un vector director puede ser → = (2, –3).
s
Además, A (1, 3) ∈s.
 x = 1 + 2t
Por tanto, s : 
 y = 3 – 3t


d) El punto medio de PQ es m ( –6 , 4 ) = (–3, 2)
2 2
→
PQ = (– 6, –4)
 m (–3, 2) ∈s
→ → → →
 d (4, –6) es un vector director de s, pues d ⊥ PQ
 x = –3 + 4t
Luego, s : 
 y = 2 – 6t

Coordenadas de puntos
8 El punto P (5, –2) es el punto medio del segmento AB, y conocemos
A (2, 3). Halla B.
☛ Si B = (x, y), ( x+2 y+3
2
,
2 )
= (5, –2 )

Si B = (x, y) 
 →
Como P es punto medio de AB 
( x + 2 , y + 3 ) = (5, –2) →
2 2

 x + 2 = 10 → x = 8 
→   → B = (8, –7)
 y + 3 = –4 → y = –7 

9 Halla el punto simétrico de P (1, –2) respecto del punto H (3, 0).
☛ H es el punto medio entre P y su simétrico.
Si P' (x, y) es simétrico de P (1, –2) respecto de H (3, 0) →
→ H es el punto medio de PP' →

→ ( x + 1 , y – 2 ) = (3, 0) →  x –+ 21 == 06 → yx == 25  → P' (5, 2)
2 2 
y
→



10 Halla las coordenadas del vértice D del paralelogramo ABCD, sabiendo
que A (1, 2), B (5, –1) y C (6, 3).
D (x, y)
Sea D (x, y).
→ →
Debe cumplirse: AB = DC
(5 – 1, –1 – 2) = (6 – x, 3 – y) → C (6, 3)
A (1, 2)
 4=6–x x=2
→  →  → D (2, 6)
 –3 = 3 – y y=6
B (5, –1)

11 Da las coordenadas del punto P que divide al segmento de extremos
→ →
A (3, 4) y B (0, –2) en dos partes tales que BP = 2 PA.
Sea P (x, y).
Sustituimos en la condición que nos imponen:


→ →
BP = 2 PA → (x – 0, y – (–2)) = 2 (3 – x, 4 – y) →

 x = 2 (3 – x)  x = 6 – 2x  3x = 6
→  →  →  →
 y + 2 = 2 (4 – y)  y + 2 = 8 – 2y  3y = 6
x=2
→  → P (2, 2)
y=2

12 Determina k para que los puntos A (–3, 5), B (2, 1) y C (6, k) estén aline-
ados.
→ →
Debe ocurrir que AB y BC sean proporcionales.
→ 
AB = (5, –4)  5 –4 –11
→  → = → 5k – 5 = –16 → k =

BC = (4, k – 1)  4 k–1 5

Distancias
13 Halla la distancia del punto P (2, –3) a las siguientes rectas:
 x = 2t 9
a)  b) y = c) 2x + 5 = 0
 y = –t 4

a) Veamos primero la ecuación implícita de la recta:

 t = x/2 x
 → = –y → x + 2y = 0
 t = –y 2
Entonces:
4 √5
dist (P, r ) = 
1 · 2 + 2 (–3)
= 
2 – 6 4
= =
√ 12 + 22 √5 √5 5
9 9
b) y = → y– =0
4 4
Por tanto:

dist (P, r ) = 
1 (– 3) – 9/4
= 
–3 – 9/4 21
=
√ 02 + 12 √1 4

c) dist (P, r ) = 
2 · 2 + 5 9
=
√2 2 + 0 2

14 Calcula la distancia del origen de coordenadas a las siguientes rectas:
a) 3x – 4y + 12 = 0 b) 2y – 9 = 0
c) x = 3 d) 3x – 2y = 0

a) dist (0, r ) = 
3 · 0 – 4 · 0 + 12 12
=
√3 2 + (–4)2 5


b) dist (0, r ) = 
2 · 0 – 9 9
=
√ 02 + 22 2

c) dist (0, r ) = 
0 – 3 3
= =3
√1 2 + 02 1

d) dist (0, r ) = 
3 · 0 – 2 · 0 0
= =0
√3 2 + 22 √ 13
(es decir, la recta 3x – 2y = 0 pasa por el origen).

15 Halla la longitud del segmento que determina la recta x – 2y + 5 = 0 al cor-
tar a los ejes de coordenadas.
Hay que calcular la distancia entre los puntos de corte de la recta con los ejes de
coordenadas.
Calculamos primero dichos puntos:

 x – 2y + 5 = 0 5
• → –2y + 5 = 0 → y = →
x=0 2

→ A 0,( 5 ) es el punto de corte con el eje Y
2

 x – 2y + 5 = 0
• → x+5=0 → x=5 →
y=0
→ B (5, 0) es el punto de corte con el eje X

—
• Luego AB = dist (A, B ) = (
(5 – 0)2 + 0 –
2)
5 2
=

= 25 +
25
4
=
√ 125
4
=
5
2
√5

16 Halla la distancia entre las rectas r : x – 2y + 8 = 0 y r' : –2x + 4y – 7 = 0.
☛ Comprueba que son paralelas; toma un punto cualquiera de r y halla su distan-
cia a r '.
1
Sus pendientes son mr = = mr ' → Son paralelas.
2
Entonces, la distancia entre r y r ' será:
dist (P, r ' ) donde P ∈r
Sea x = 0.
–8
Sustituyendo en r → y = = 4 → P (0, 4) ∈r
–2
Así:
9 √5
dist (r, r ' ) = dist (P, r ' ) = 
–2 · 0 + 4 · 4 – 7
= 
16 – 7 9
= =
√ (–2)2 + 42 √ 20 2 √5 10


17 Determina c para que la distancia de la recta x – 3y + c = 0 al punto (6, 2)
sea de √10 unidades. (Hay dos soluciones).

dist (P, r ) = 
1 · 6 – 3 · 2 + c
= 
6 – 6 + c
=   = √ 10
c
√1 + 9 √ 10 √ 10
 c = √ 10 → c = 10
 1
 √ 10
Hay dos soluciones: 
 c = – √ 10 → c = –10
 2 =0
 √ 10 – 3y
+ 10
x
P
Las dos rectas solución serán dos rectas paralelas:
0=0
y–1
x–3

18 Calcula el valor de a para que la distancia del punto P (1, 2) a la recta
ax + 2y – 2 = 0 sea igual a √2 .

dist (P, r ) = √ 2 → 
a · 1 + 2 · 2 – 2
= √2 →
√a 2 + 4
 a+2
 = √ 2 → a + 2 = √ 2 (a 2 + 4)
 √a 2 + 4
⇒ 
 a + 2 = – √ 2 → a + 2 = – √ 2 (a 2 + 4)

 √a + 4
2

Al elevar al cuadrado obtenemos la misma ecuación en ambos casos.
→ (a + 2)2 = 2 (a 2 + 4) → a 2 + 4a + 4 = 2a 2 + 8 →
4 ± √ 16 – 16
→ a 2 – 4a + 4 = 0 → a = =2
2

Página 208

Ángulos
19 Halla el ángulo que forman los siguientes pares de rectas:
 y = 2x + 5  3x – 5y + 7 = 0
a)  b) 
 y = – 3x + 1  10x + 6y – 3 = 0
 x = 3 – t  x = –1 – 3t  2x – y = 0
c)   c) 
 y = 2t y=4+t  2y + 3 = 0

a) r : y = 2x + 5  → sus pendientes son:  mr = 2
  m = –3
s : y = –3x + 1   s
mr – ms
 1 + m m  =  1 + 2 (–3)  =  –5  = 1 → α = 45°
2 – (–3) 5
tg α =
r s


→
b) v = (3, –5) ⊥ r1 
 → →
→  → α ≡ r1 r2 = v, w →
w = (10, 6) ⊥ r2 

→ →
v · w  30 – 30
→ cos α = = = 0 → α = 90°
→ → → →
 v  w   v  w 

c) Los vectores directores de esas rectas son:
→ →
d1 = (–1, 2) y d2 = (–3, 1)
Entonces:
→ →
d1 · d2 √ 2 → α = 45°
cos α = → → = 
3 + 2 5 1
— — = = =
d1 d2 √ 5 · √10 5 √2 √2 2

→
d) a1 = (2, –1) ⊥ r1 
 → →
→  → α ≡ r1 r2 = a1, a2 →
a2 = (0, 2) ⊥ r2 

→ →
 a1 · a2
0 – 2 2 1 √5 =
→ cos α = → → = — — = = =
 a1 a2 √5 · √4 √5 · 2 √5 5

≈ 0,4472 → α = 63° 26' 5,82"

20 ¿Qué ángulo forma la recta 3x – 2y + 6 = 0 con el eje de abscisas?
☛ No es necesario que apliques ninguna fórmula. Sabes que la pendiente de r es la
tangente del ángulo que forma r con el eje de abscisas. Halla el ángulo con la pen-
diente de r.

3
La pendiente de r es mr = .
2
La pendiente de r es, además, tg α:
3
mr = tg α → tg α = → α = 56° 18' 35,8"
2

Y
r

α
X


21 ¿Qué ángulo forma la recta 2x – y + 5 = 0 con el eje de ordenadas?
☛ El ángulo pedido es el complementario del ángulo que la recta forma con el eje
de abscisas.
1
El ángulo pedido, α, es complementario de β → tg β =
tg α
Por otro lado, tg β = mr = 2:
1 1
tg α = = → α = 26° 33' 54,2"
tg β 2

Y r

α

X
β

22 Calcula n de modo que la recta 3x + ny – 2 = 0 forme un ángulo de 60° con
el OX. 
Y tg 60° = √ 3 

r
3  Como tg 60° = mr , se tiene que:
mr = – 
n

60°
3 –3 –3 √ 3
X √3 = – → n= = = – √3
n √3 3

PARA RESOLVER
23 Calcula m y n en las rectas de ecuaciones:
r : mx – 2y + 5 = 0 s : nx + 6y – 8 = 0
sabiendo que son perpendiculares y que r pasa por el punto P (1, 4).
☛ Las coordenadas de P deben verificar la ecuación de r. Así calculas m. Expre
sa la perpendicularidad con vectores o con pendientes y halla n.
• P (1, 4) ∈r → m · 1 – 2 · 4 + 5 = 0 → m = 3

• (m, –2) ⊥ r 


(n, 6) ⊥ s  → (m, –2) ⊥ (n, 6) →

Como deben ser r ⊥ s 

→ (m, –2) · (n, 6) = 0 → m · n + (–2) · 6 = 0 →
→ 3n – 12 = 0 → n = 4


m –n
NOTA: Usando las pendientes mr = y ms = , para que r ⊥ s debe ser
2 6
mr · ms = –1, es decir:

( )
;;;
m –n
· = –1 → –mn = –12 → –3n = –12 → n = 4
2 6

;;;
24 Halla las ecuaciones de las rectas r, s, t y p. Y 30°

Y t s

;;;
s
t p p X
30° r

r

30°

180° – β
α β
X

r

• p : Pasa por los puntos (–3, –3) y (1, 4).
Así, su pendiente es:
4 – (–3) 7
m= =
1 – (–3) 4
Por tanto:
7
p: y = 1 + (x – 4) → 7x – 4y + 9 = 0
4

• r : Su pendiente es 0 y pasa por el punto 0, ( –3
2).
Por tanto:
3
r: y = –
2

• s : Su vector director es (0, 1) y pasa por (2, 0).
Por tanto:
x=2
s: 
y=t

• t : Pasa por los puntos (1, 0) y (–3, 2).
Así, su pendiente es:
2–0 2 1
m= = =–
–3 – 1 –4 2
Por tanto:
1
t: y = – (x – 1) → x + 2y – 1 = 0
2


 x = –1 + 3t
25 Dada la recta r :  halla k de modo que r sea paralela a la
 y = 2 + kt
bisectriz del segundo cuadrante.

 x = –t
• La bisectriz del segundo cuadrante es x = –y →  (en paramétricas).
→ y=t
Su vector director es d = (–1, 1).
→
• El vector director de r es r = (3, k ).

• Como queremos que r // bisectriz del segundo cuadrante, entonces sus vectores
directores deben ser proporcionales:
–1 1
= → k = –3
3 k

26 En el triángulo de vértices A(–2, 3), B (5, 1), C (3, –4), halla las ecuaciones de:
a) La altura que parte de B.
b) La mediana que parte de B.
c) La mediatriz del lado CA.

a) La altura que parte de B, hB, es una recta perpendicular a AC que pasa por el
punto B: 
→ 
hB ⊥ AC (5, –7) → el vector director de hB es hB (7, 5) 
→ 
B (5, 1) ∈hB 
 x–5
t=
 x = 5 + 7t  7 x–5 y–1
→ hB :  →  → = →
 y = 1 + 5t t= y–1 7 5
 5

→ hB : 5x – 7y – 18 = 0

b) mB (mediana que parte de B ) pasa por B y por el punto medio, m, de AC :

( –2 2+ 3 , 3 – 4 ) = ( 1 , – 1 ) ∈m


m B 
2 2 2 →

B (5, 1) ∈mB 

( ) ( ) es vector director de m .
→ 1 1 9 3
→ mB 5 – , 1 + = , B
2 2 2 2

Luego: x=5+ 9
 t  2x = 10 + 9t
2
mB : 
 → 
 →
y=1+ 3
t  t = 2y – 2
 2  3



 t = 2x – 10
 9
 2x – 10 2y – 2
→  → = → mB : 6x – 18y – 12 = 0
t= 2y – 2 9 3
 3

c) La mediatriz de CA, z, es perpendicular a CA por el punto medio del lado,
m'. Así:

→ →
CA = (–5, 7) ⊥ z → vector director de z : z (7, 5)


→
( ) ( )

3 – 2 –4 + 3 1 1
m' , = ,– ∈z 
2 2 2 2
 1  2x – 1
x = + 7t t =
 2  14 2x – 1 2y + 1
→ z:  →  → = →
 y = – 1 + 5t t = 2y + 1 14 10
 2  10
 

→ z : 20x – 28y – 24 = 0 → z : 5x – 7y – 6 = 0

27 La recta 2x + 3y – 6 = 0 determina, al cortar a los ejes de coordenadas, un
segmento AB.
Halla la ecuación de la mediatriz de AB.
☛ Después de hallar los puntos A y B, halla la pendiente de la mediatriz, inversa y
opuesta a la de AB. Con el punto medio y la pendiente, puedes escribir la ecuación.

Y

A

B
X

 2x + 3y – 6 = 0
• A = r I eje Y :  → 3y – 6 = 0 → y = 2 → A (0, 2)
x=0

 2x + 3y – 6 = 0
• B = r I eje X :  → 2x – 6 = 0 → x = 3 → B (3, 0)
y=0
→ →

• AB = (3, –2) ⊥ mAB (mediatriz de AB ) → mAB = (2, 3) 

→
( 3 , 2 ) = ( 3 , 1) (punto medio de AB ) ∈mediatriz

mAB 
2 2 2

2 (
x– ) → y=
3 3 3 5
→ y–1= x– → m : 6x – 4y – 5 = 0
AB
2 2 4


28 Determina los puntos que dividen al segmento AB, A (–2, 1), B (5, 4), en tres
partes iguales.
→ 1 →
☛ Si P y Q son esos puntos, AP = AB.
3
→ → —
Escribe las coordenadas de AP y de AB y obtén P. Q es el punto medio de PB

B
Q
P
A

→ 1 → 1
• AP = AB → (x + 2, y – 1) = (7, 3) →
3 3
 7 7 1
x+2= → x= –2=
→ 

y–1=
3
3
3
→ y= 1 + 1 = 2
3
→ P ( 1 , 2)
3
 3


• Q es un punto medio de PB → Q ( 1/32+ 5 , 2 + 4 ) → Q ( 8 , 3)
2 3

→ →
29 ¿Qué coordenadas debe tener P para que se verifique que 3 PQ – 2 QR = 0,
siendo Q (3, 2) y R (–1, 5)?
→ →
3 PQ = 2 QR → 3 (3 – x, 2 – y ) = 2 (–4, 3) →

 x = 17
 9 – 3x = –8
→ 
 6 – 3y = 6

→ 
y= 0
3 → P 17 , 0
3 ( )


30 Los puntos medios de los lados de cualquier cuadrilátero forman un parale-
logramo. Compruébalo con el cuadrilátero de vértices:
A (3, 8) B (5, 2) C (1, 0) D (–1, 6)

B P ( 5 + 3 , 8 + 2 ) = (4, 5)
2 2
P Q (3, 1); R (0, 3); S (1, 7)

→ 
A PQ = (3 – 4, 1 – 5) = (–1, –4)  → →
→  PQ = SR
Q 
S SR = (0 – 1, 3 – 7) = (–1, –4)

→ 
D SP = (4 – 1, 5 – 7) = (3, –2)  → →
→  SP = RQ
R RQ = (3 – 0, 1 – 3) = (3, –2) 
C


31 Halla el pie de la perpendicular trazada desde P (1, –2) a la recta
r : x – 2y + 4 = 0.
☛ Escribe la perpendicular a r desde P y halla el punto de corte con r.

P (1, –2) r : x – 2y + 4 = 0

P' (x, y)

s

→
Sea s la recta perpendicular a r desde P y r = (2, 1) vector director de r.
→ → → → → →
Así, PP' ⊥ r ⇒ el vector director de s, s, también es perpendicular a r ( s ⊥ r ),
→
luego podemos tomar s (1, –2). Como P (1, –2) ∈s :

x=1+t → t=x–1
 y+2
s:  y+2 → x–1= → –2x + 2 = y + 2 →
 y = –2 – 2t → t = –2 –2

→ s : 2x + y = 0
El punto P' (x, y) es tal que:
 s : 2x + y = 0 → y = –2x
P' = s I r 
 r : x – 2y + 4 = 0

Sustituyendo en la segunda ecuación:
x – 2 (–2x) + 4 = 0 → x + 4x + 4 = 0 →

→ x=
–4
5
→ y = –2
–4
5 ( )
=
8
5
Luego: P' ,(
–4 8
5 5 )
32 Las ecuaciones de los lados del triángulo ABC son AB: x + 2y – 4 = 0,
AC : x – 2y = 0, BC: x + y = 0. Halla:
a) Los vértices del triángulo.
b) El vector que une los puntos medios de AB y AC. Comprueba que es
→
paralelo a BC.
→
☛ b) Las coordenadas de BC deben ser proporcionales a las del vector que has ha-
llado.


A

B C

a) A = AB I AC
B = AB I BC
C = AC I BC

 AB : x + 2y – 4 = 0
• A: 
 AC : x – 2y =0 Sumamos las ecuaciones:
2x –4=0 → x=2
Sustituyendo en AC : 2 – 2y = 0 → y = 1
Luego: A (2, 1)

 
• B :  AB : x + 2y – 4 = 0  →
 BC : x + y = 0 → x = –y 

→ –y + 2y – 4 = 0 → y = 4 → x = –4
Luego: B (–4, 4)

 
• C :  AC : x – 2y = 0  →
 BC : x + y = 0 → x = –y 

→ –y – 2y = 0 → y = 0 → x = 0
Luego: C (0, 0)

b) El punto medio de AB es MAB –1, ( 5 ).2

El punto medio de AC es MAC

(1, 1 ).
2
→ 
MAB MAC = (2, –2)  → → → 1 →
Así, MAB MAC // BC, pues: MAB MAC = BC
→  2
BC = (4, –4) 

33 Halla el área del cuadrilátero de vértices:
A (– 4, 3), B (0, 5), C (4, –2) y D (–3, –2)
☛ Traza una diagonal para descomponerlo en dos triángulos de la misma base.


B (0, 5)

A (–4, 3)

D (–3, –2) C (4, –2)

• La diagonal AC divide el cuadrilátero en dos triángulos con la misma base, cuya
medida es:
→
AC  = (8, –5) = √ 89

• Sean hB y hD las alturas desde B y D, respectivamente, a la base:
hB = dist (B, r ) y hD = dist (D, r )
→
donde r es la recta que contiene el segmento AC .
→
Tomando como vector director de r el vector AC, la ecuación de dicha recta es:
5x + 8y + k = 0 
 –20 + 24 + k = 0 ⇒ k = –4 ⇒ r : 5x + 8y – 4 = 0
Como (–4, 3) ∈r 

Luego:
hB = dist (B, r ) = 
5 · 0 + 8 · 5 – 4 36
=
√ 89 √ 89

hD = dist (D, r ) = 
5 (–3) + 8 (–2) – 4 35
=
√ 89 √ 89
• Así:
b · hB b · hD b
AABCD = AABC + AADC = + = (h + hD ) =
2 2 2 B

=
√ 89
2 ( 36
√ 89
+
35
√ 89 ) =
71
2

34 Calcula el área del triángulo cuyos lados están sobre las rectas:
r: x = 3 s : 2x + 3y – 6 = 0 t: x – y – 7 = 0
r s
A

C
B t


x=3
•A = r I s  → 6 + 3y – 6 = 0 → y = 0
 2x + 3y – 6 = 0
Luego: A (3, 0)

x=3
•B = r I t  → 3 – y – 7 = 0 → y = –4
x–y–7=0
Luego: B (3, –4)

 2x + 3y – 6 = 0
•C = s I t  →
x–y–7=0 → x=y+7
→ 2 (y + 7) + 3y – 6 = 0 →
–8
→ 2y + 14 + 3y – 6 = 0 → 5y + 8 = 0 ⇒ y = →
5
–8 27
→ x= +7=
5 5

Luego: C ( 27 , –8 )
5 5

• Consideramos el segmento AB como base:
→
AB  = (0, –4) = √ 16 = 4

• La altura desde C es hC = dist (C, r ) = 
(–8/5) – 3 23
=
√1 2 + 02 5
• Así:
→
AB · hC 4 · 23/5 46
Área = = =
2 2 5

Página 209
35 Traza, por el punto B (0, 5), una recta de pendiente 1/3. Por el punto
C (5, 0), traza una recta perpendicular a la anterior. Se cortan en un punto
A. Halla el área de triángulo ABC .

r
A (3, 6)
B (0, 5)

r

C (5, 0)

1 1
• Sea r la recta por A y B. Su pendiente es mr = → r: y = x + 5
3 3


• Sea s la recta por A y C. Su pendiente es ms = –3 (pues r ⊥ s ):
s : y – 0 = –3 (x – 5) → s : y = –3x + 15

 y = (1/3) x + 5 1
•A = r I s  → x + 5 = –3x + 15 →
 y = –3x + 15 3
10 1
→ x = 10 → x = 3 → y = ·3+5=6
3 3
Luego: A (3, 6)
→
• La base del triángulo es: AB = (–3, –1) = √ 10
→
La altura es: AC = (2, –6) = √ 40 = 2 √ 10
→ → — —
AB AC √ 10 · 2 √ 10 = 10
El área es: AABC = =
2 2

36 En el triángulo de vértices A (–1, –1), B (2, 4) y C (4, 1), halla las longitudes
de la mediana y de la altura que parten de B.
• Mediana. Es el segmento BM donde M es el punto medio de AC.

M ( 3 , 0) → BM = ( 3 – 2, 0 – 4) = (– 1 , –4)
2
→
2 2

→ √ 65
La longitud de la mediana es: BM  = √ 1/4 + 16 =
2

• Altura. Es el segmento BP donde P es el pie de la perpendicular a AC desde B.
→
AC = (5, 2) ⇒ la recta que contiene ese segmento es:

 x = –1 + 5t x+1 y+1
r:  → = → 2x – 5y – 3 = 0
 y = –1 + 2t 5 2

→ →
v = (–2, 5) ⊥ AC ⇒ la recta s ⊥ r que pasa por B:

 x = 2 – 2t x–2 y–4
s:  → = → 5x + 2y – 18 = 0
 y = 4 + 5t –2 5

 r : 2x – 5y – 3 = 0
P=rIs → 
 s : 5x + 2y – 18 = 0
Multiplicamos la primera por 2 y la segunda por 5, y sumamos:
4x – 10y – 6 = 0
25x + 10y – 90 = 0
96
29x – 96 = 0 → x = →
29


96 192 105
→ 2· – 5y – 3 = 0 → 5y = –3= →
29 29 29
105 21
→ y= :5=
29 29

Luego: P ( 96 , 21 )
29 29

= BP = (
 29 , – 29 ) = √ 29 ≈ 29 ≈ 3,528
→ 38 95 10 469 √ 10 469
Así: hB 2

37 Halla el punto de la recta 3x – 4y + 8 = 0 que equidista de A (–6, 0) y B (0, –6).

P

r
A (–6, 0)

B (0, –6)

P (x, y ) debe verificar dos condiciones:
1. P (x, y ) ∈r ⇒ 3x – 4y + 8 = 0
2. dist (A, P ) = dist (B, P ) ⇒ √ (x + 6)2 + y 2 = √ x 2 + (y + 6)2

 3x – 4y + 8 = 0  3x – 4y + 8 = 0
→  →  →
 x 2 + 12x + 36 + y 2 = x 2 + y 2 + 12y + 36 x=y
→ 3x – 4x + 8 = 0 → x = 8 = y → P (8, 8)

38 Determina un punto en la recta y = 2x que diste 3 unidades de la recta
3x – y + 8 = 0.

 P (x, y ) ∈r : y = 2x
 →
 dist (P, r ' ) = 3, donde r ' : 3x – y + 8 = 0

 y = 2x

→ 
3x – 2x + 8
=3 → 
x + 8
→  3x – y + 8 =3 →
 =3 √ 10 √ 10
 √ 10

x + 8 = 3 √ 10 → x1 = 3 √ 10 – 8 →

→ dos posibilidades: 

 x + 8 = –3 √ 10 → x2 = –3 √ 10 – 8 →


 → y1 = 6 √ 10 – 16  P1 (3 √ 10 – 8, 6 √ 10 – 16)
 
 →
 → y2 = –6 √ 10 – 16  P2 (–3 √ 10 – 8, –6 √ 10 – 16)
 

r'

P1

P2 r

39 Halla los puntos de la recta y = –x + 2 que equidistan de las rectas x + 2y – 5 = 0
y 4x – 2y + 1 = 0.
Sean r1, r2 y r3 las tres rectas del ejercicio, respectivamente.
Buscamos los puntos P (x, y ) que cumplan:

 P ∈r1 ⇒ y = –x + 2
 dist (P, r ) = dist (P, r ) → x + 2y – 5 x – 2y + 1 →
 2 3 = 4
√5 √ 20
→ 
x + 2 (–x + 2) – 5 4x – 2 (–x + 2) + 1
= →
√5 2 √5


 –x – 1 = 6x – 3 , o bien
→ –x – 1 = 6x – 3 →  2 →

2  –6x + 3
 –x – 1 =
 2

 –2x – 2 = 6x – 3, o bien  8x = 1  x = 1/8
→  →  →  1 →
 –2x – 2 = –6x + 3  4x = 5  x2 = 5/4


 y1 = – 1 + 2 = 15
→ 

8

P
8 →  1

( 1 , 15 )
8 8


5
 y2 = – + 2 =
4
3
4

 P2
 (5, 3)
4 4

40 Calcula c para que la distancia entre las rectas 4x + 3y – 6 = 0 y 4x + 3y + c = 0
sea igual a 3.
Sea P ∈r1 donde x0 = 0 → y0 = 2 → P (0, 2) ∈r1

Así, dist (r1, r2) = dist (P, r2) = 
4 · 0 + 3 · 2 + c
=3 →
√ 16 + 9
 6 + c = 15 → c1 = 9
→ 
6 + c
=3 → 
5  6 + c = –15 → c2 = –21


41 El lado desigual del triángulo isósceles ABC, tiene por extremos A (1, –2) y
B (4, 3).
El vértice C está en la recta 3x – y + 8 = 0.
Halla las coordenadas de C y el área del triángulo.
→
• La recta del lado desigual (base) tiene como vector director AB = (3, 5):

 x = 1 + 3t x–1 y+2
r:  → = → r : 5x – 3y – 11 = 0
 y = –2 + 5t 3 5
→ →
• La recta que contiene la altura tiene por vector director a = (–5, 3) ⊥ AB y pasa

por el punto medio del lado desigual AB, es decir, por m ( 5 , 1 ):
2 2
 x = 5/2 – 5t 2x – 5 2y – 1
hc :  → = →
 y = 1/2 + 3t –10 6
→ hc : 12x + 20y – 40 = 0 → hc : 6x + 10y – 20 = 0

• C = s I hc donde s : 3x – y + 8 = 0
 3x – y+ 8=0  –6x + 2y – 16 = 0
 → 
 6x + 10y – 20 = 0  6x + 10y – 20 = 0
36
12y – 36 = 0 → y = =3 →
12
–5
→ 3x – 3 + 8 = 0 → 3x + 5 = 0 → x =
3

Luego: C ( –5 , 3)
3
→ →
AB Cm (*) √ 34 · (√ 850/6)
— —
base × altura
• Área = = = ≈ 14,17
2 2 2

 → →
 AB = (3, 5) →  AB = √ 34

(*)

( ) → Cm =

 → –25 –5 → √ 850
 Cm ,
6 2 6

42 Dos casas están situadas en los puntos A(4, 0) y B(0, 3). Se quiere construir un
pozo que esté a la misma distancia de A y de B, y a 8 m de una tubería que une
A y B. ¿Cuál es el lugar adecuado?

La recta que une A y B tiene por vector director:
→  x = 4 – 4t x–4 y
AB = (–4, 3) → r :  → = → r : 3x + 4y – 12 = 0
 y = 3t –4 3

El pozo debe estar en un punto P (x, y ) tal que:


 dist (P, r ) = 8
 →
 dist (P, A) = dist (P, B )

 3x + 4y – 12 3x + 4y – 12
 = =8

→  √ 9 + 16 5 →

 √ (x – 4)2 + y 2 = √ x 2 + (y – 3)2 → x 2 – 8x + 16 + y 2 = x 2 + y 2 – 6y + 9

 3x + 4y – 12 = 40
→ 
 6y + 7 →
 –8x + 16 = –6y + 9 → x =
 8

 
6y + 7
→ 3· + 4y – 12 = 40 → 18y + 21 + 32y – 96 = 320 →
8

 50y – 75 = 320
→ 50y – 75 = 320 →  →
 50y – 75 = –320

 320 + 75 79 6 · (79/10) + 7 (474 + 70)/10 34
 y1 = = → x1 = = =

→ 
50 10 8 8 5
 –320 + 75 –49 6 · (–49/10) + 7 –14
 y2 = = → x2 = =
 50 10 8 5

Luego: P1 ( 34 , 79 ), P ( –14 , –49 )
5 10 2
5 10
(Son dos puntos de la mediatriz del segmento AB ).

P1

B

A

P2

43 Halla la ecuación de la recta que pasa por el punto de intersección de las
rectas r y s y forma un ángulo de 45° con la recta: x + 5y – 6 = 0.
r : 3x – y – 9 = 0 s: x – 3 = 0

 3x – y – 9 = 0
P = r I s:  → 9–y–9=0 → y=0
 x –3=0

Luego: P (3, 0)


Como la recta pedida y x + 5y – 6 = 0 forman un ángulo de 45°, entonces si sus
pendientes son, respectivamente, m1 y m2, se verifica:

   →
m2 – m1 (–1/5) – m1
tg 45° = → 1=
1 + m2 · m1 1 + (–1/5) · m1

 →
–1 – 5 · m1
→ 1=
5 – m1

 5 – m1 = –1 – 5m1, o bien
→  →
 – (5 – m1) = –1 – 5m1

 4m1 = –6 → m1 = –6/4
→ 
 6m1 = 4 → m1 = 4/6

–6 –3 9
Hay dos posibles soluciones: t1 : y – 0 = (x – 3) → t1 : y = x+
4 2 2

4 2 6
t2 : y – 0 = (x – 3) → t2 : y = x–
6 3 3

44 Dadas las rectas:
r : 2x – 5y – 17 = 0 s: 3x – ky – 8 = 0
Calcula el valor de k para que r y s se corten formando un ángulo de 60°.
☛ Halla la pendiente de r. La pendiente de s es 3/k. Ten en cuenta que obtendrás
dos soluciones.

Las pendientes de r y s son, respectivamente:
2 3
mr = y ms =
5 k
Entonces:

   →
2/5 – 3/k 2k – 15
tg 60° = → √3 = dos casos:
1 + 2/5 · 3/k 5k + 6
 

 √ 3 (5k + 6) = 2k – 15 → 5 √ 3 k + 6 √ 3 = 2k – 15 

→   →
 
– √ 3 (5k + 6) = 2k – 15 → –5 √ 3 k – 6 √ 3 = 2k – 15

–15 – 6 √ 3 –15 + 6 √ 3
→ k1 = , k2 =
5 √3 – 2 –5 √ 3 – 2


45 Las rectas r : 3x – 2y + 6 = 0, s: 2x + y – 6 = 0 y t: 2x – 5y – 4 = 0 son los
lados de un triángulo. Represéntalo y halla sus ángulos.
3 Y
mr =
2

ms = –2;

2
mt =
5

 1 + 3/2 · (–2)  =
3/2 – (–2) 7/2 7 X
tg (r, s ) = =
2 4
t r s
Luego: (r, s ) = 60° 15' 18,4"

 1 + 3/2 · 2/5  =  10 + 6  = 16
3/2 – 2/5 15 – 4 11
tg (r, t ) =

Luego: (r, t ) = 34° 30' 30,7"

Por último, (s, t ) = 180° – (r, s ) – (r, t ) = 85° 14' 11"

46 Halla los ángulos del triángulo cuyos vértices son A(–3, 2), B(8, –1) y C(3, –4).
☛ Representa el triángulo y observa si tiene algún ángulo obtuso.
→ → Y
AB = (11, –3); BA (–11, 3)
→ →
AC = (6, – 6); CA (–6, 6) A (–3, 2)
→ → X
BC = (–5, –3); CB (5, 3)
B (8, –1)
→ →
^ AB · AC 66 + 18
cos A = = — — ≈ 0,868
→ → √130 √ 72 C (3, –4)
AB AC

^
Luego: A = 29° 44' 41,6"

→ →
^ BA · BC 55 – 9
cos B = = — — ≈ 0,692
→ → √130 √ 34
BA BC

^
Luego: B = 46° 13' 7,9"
^ ^ ^
Así, C = 180° – ( A + B) = 104° 2' 10,5"


47 Halla la ecuación de la recta que pasa por el punto (0, 2) y forma un ángulo
de 30° con la recta x = 3.
☛ La recta que buscamos forma un ángulo de 60° o de 120° con el eje OX.

Y La recta r forma un ángulo de 60° o de 120° con el eje
r2 OX.
Su pendiente es:
 m1 = tg 60° = √ 3 , o bien

30°
x=3 
 m2 = tg 120° = – √ 3

(0, 2)
120°
X
Teniendo en cuenta que debe pasar por P (0, 2), las
60° posibles soluciones son:

r1 : y = √ 3 x + 2

r1 r2 : y = – √ 3 x + 2

48
1
La recta 2x + y = 0 es la bisectriz de un ángulo recto cuyo vértice es – , 1 .
2 ( )
Halla las ecuaciones de los lados del ángulo.
Las pendientes de las tres rectas son:
mb = –2, mr , mr '

r

b: 2x + y = 0
45°
(
1
V – —, 1
2 ) 45°

r'

   →
mb – mr –2 – mr
tg 45° = → 1=
1 + mb mr 1 – 2mr

 1 – 2mr = –2 – mr → mr = 3
→  →
 –1 + 2mr ' = –2 – mr ' → mr ' = –1/3
 1
(
 r : y – 1 = 3 x + 2 → y = 3x + 2

5
)
→ 
 –1 1
( –1
 r': y – 1 = 3 x + 2 → y = 3 x + 6

5
)

49 Encuentra un punto en la recta x – 2y – 6 = 0 que equidiste de los ejes de
coordenadas.

Eje X : y = 0 
  dist (P, eje X ) = dist (P, eje Y )
Eje Y : x = 0  →  →
P (x, y ) ∈r   x – 2y – 6 = 0


y x x=y
= → dos casos: 
→ √0 2 + 12 √0 2 + 12  x = –y →
x – 2y – 6 = 0

 y – 2y – 6 = 0 → y1 = –6 → x1 = –6  P (–6, –6)
→  →  1
 – y – 2y – 6 = 0 → y2 = –2 → x2 = 2  P2 (2, –2)

Y
r

X

P2

P1

50 Halla las ecuaciones de las rectas que pasan por A (–2, 2) y forman un án-
gulo de 60° con la recta x = y.

b : x = y → su pendiente es mb = 1

 1 + 1 · m  → √3 =  1 + m  →
1–m 1–m
tg 60° =

 √3 + √3 m = 1 – m → m = 1 – √3
 1
 √3 + 1
→ 
 1 + √3
 – √ 3 – √ 3 m = 1 – m → m2 =
 –√ 3 + 1

Teniendo en cuenta que pasan por A (–2, 2):

1 – √3
r1 : y – 2 = (x + 2)
√3 + 1
ECUACIONES PUNTO-PENDIENTE
1 + √3
r2 : y – 2 = (x + 2)
–√ 3 + 1


Soluciones unidad 8

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Destacado

Destacado (14)

Similar a Soluciones unidad 8

Similar a Soluciones unidad 8 (20)

Más de klorofila

Más de klorofila (20)

Soluciones unidad 8