Descargar como PDF, PPTX
Subido porFrancisco Sandoval
1_introduccion_Campos_Electromagneticos
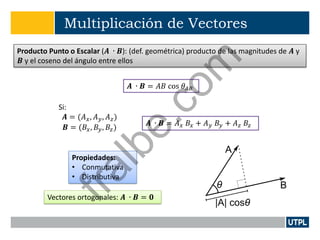
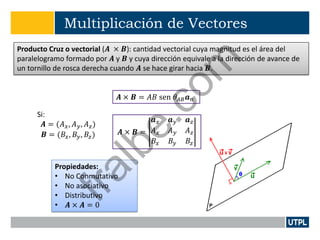
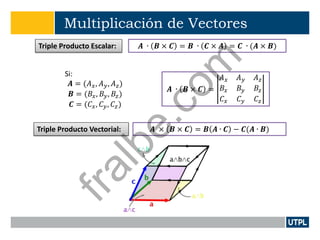
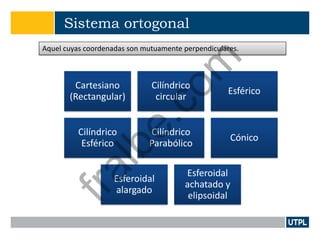
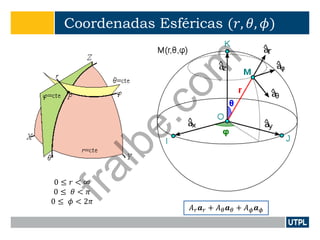
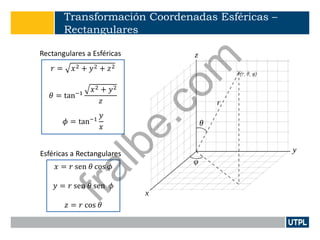
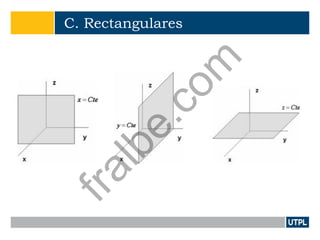
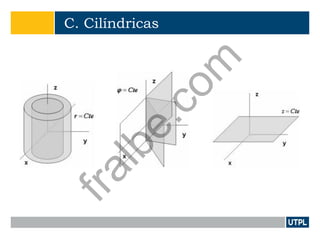
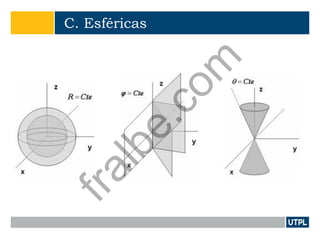
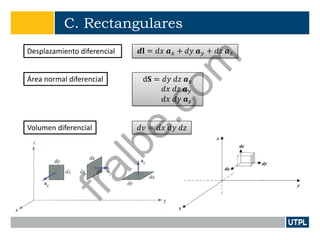
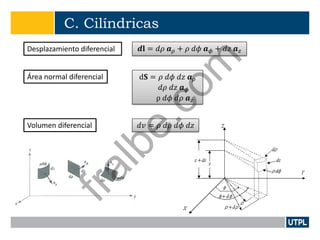
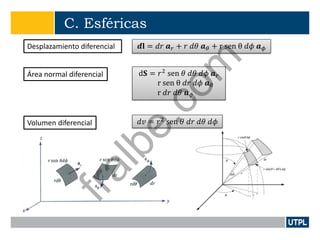
Este documento presenta una introducción a la teoría de campos electromagnéticos. Explica conceptos básicos como vectores, sistemas de coordenadas, cálculo vectorial y sus aplicaciones a campos electromagnéticos. También incluye definiciones de electromagnetismo, dispositivos electromagnéticos, álgebra vectorial, sistemas de coordenadas y transformaciones, y cálculo aplicado a vectores.
Más contenido relacionado
Similar a 1_introduccion_Campos_Electromagneticos
1_introduccion_Campos_Electromagneticos
- 1. Francisco A. Sandoval Teoríade Campos Electromagnéticos 2014 fralbe.com
- 2. Agenda • Preámbulo • Presentacióndel Plan Académico • Introducción – Algebra vectorial. – Sistemas de Coordenadas y su transformación. – Cálculo aplicado a vectores. fralbe.com
- 3.
- 4. Def. Electromagnetismo Electromagnetismo esla rama de la física o ingeniería que estudia los fenómenos eléctricos y magnéticos. microondas antenas Maquinaria eléctrica Comunicaciones satelitales Investigación nuclear Fibra óptica Interferencia y Compatibilidad electromagnéticas Meteorología por radar … fralbe.com
- 5. Dispositivos Electromagnéticos Transformadores RadiosTelevisores Teléfonos Motores Eléctricos Líneas de Transmisión Guías de Ondas Antenas Fibra óptica Radares Rayos láser fralbe.com
- 6.
- 7. Escalares y Vectores Escalar:cantidad que sólo posee magnitud. Vector: cantidad que posee tanto magnitud como dirección. Campo: función que especifica una cantidad particular en cualquier parte de una región. • Tiempo • Masa • Distancia • Temperatura • … • Velocidad • Fuerza • Intensidad del campo eléctrico • desplazamiento fralbe.com
- 8. Vector Unitario • Vector𝑨: magnitud (escalar 𝑨 ) y dirección. • Vector unitario 𝒂 𝐴: vector cuya magnitud equivale a la unidad y cuya dirección sigue la dirección de 𝑨. 𝒂 𝐴 = 𝑨 𝑨 • Representación • Componentes fralbe.com
- 9. Adición y Sustracciónde Vectores SUMA SUSTRACCIÓN Regla del paralelogramo Regla del triángulo Regla del triángulo Propiedades: • Conmutativa • Asociativa • Distributiva fralbe.com
- 10. Multiplicación de Vectores ProductoPunto o Escalar (𝑨 ∙ 𝑩): (def. geométrica) producto de las magnitudes de 𝑨 y 𝑩 y el coseno del ángulo entre ellos 𝑨 ∙ 𝑩 = 𝐴𝐵 cos 𝜃 𝐴𝐵 Si: 𝑨 = (𝐴 𝑥, 𝐴 𝑦, 𝐴 𝑧) 𝑩 = (𝐵𝑥, 𝐵𝑦, 𝐵𝑧) 𝑨 ∙ 𝑩 = 𝐴 𝑥 𝐵𝑥 + 𝐴 𝑦 𝐵𝑦 + 𝐴 𝑧 𝐵𝑧 Propiedades: • Conmutativa • Distributiva Vectores ortogonales: 𝑨 ∙ 𝑩 = 𝟎 fralbe.com
- 11. Multiplicación de Vectores ProductoCruz o vectorial (𝑨 × 𝑩): cantidad vectorial cuya magnitud es el área del paralelogramo formado por 𝑨 y 𝑩 y cuya dirección equivale a la dirección de avance de un tornillo de rosca derecha cuando 𝑨 se hace girar hacia 𝑩. 𝑨 × 𝑩 = 𝐴𝐵 sen 𝜃 𝐴𝐵 𝒂 𝑛 Si: 𝑨 = (𝐴 𝑥, 𝐴 𝑦, 𝐴 𝑧) 𝑩 = (𝐵𝑥, 𝐵𝑦, 𝐵𝑧) 𝑨 × 𝑩 = 𝒂 𝑥 𝒂 𝑦 𝒂 𝑧 𝐴 𝑥 𝐴 𝑦 𝐴 𝑧 𝐵𝑥 𝐵𝑦 𝐵𝑧 Propiedades: • No Conmutativo • No asociativo • Distributivo • 𝑨 × 𝑨 = 0 fralbe.com
- 12. Multiplicación de Vectores TripleProducto Escalar: 𝑨 ∙ 𝑩 × 𝑪 = 𝑩 ∙ 𝑪 × 𝑨 = 𝑪 ∙ (𝑨 × 𝑩) Si: 𝑨 = (𝐴 𝑥, 𝐴 𝑦, 𝐴 𝑧) 𝑩 = (𝐵𝑥, 𝐵𝑦, 𝐵𝑧) 𝑪 = (𝐶 𝑥, 𝐶 𝑦, 𝐶𝑧) 𝑨 ∙ 𝑩 × 𝑪 = 𝐴 𝑥 𝐴 𝑦 𝐴 𝑧 𝐵𝑥 𝐵𝑦 𝐵𝑧 𝐶 𝑥 𝐶 𝑦 𝐶𝑧 𝑨 × 𝑩 × 𝑪 = 𝑩 𝑨 ∙ 𝑪 − 𝑪(𝑨 ∙ 𝑩)Triple Producto Vectorial: fralbe.com
- 13. SISTEMAS DE COORDENADASY SU TRANSFORMACIÓN fralbe.com
- 14. Sistema ortogonal Aquel cuyascoordenadas son mutuamente perpendiculares. Cartesiano (Rectangular) Cilíndrico circular Esférico Cilíndrico Esférico Cilíndrico Parabólico Cónico Esferoidal alargado Esferoidal achatado y elipsoidal fralbe.com
- 15. Coordenadas Cartesianas (x,y, z) 𝐴 𝑥 𝒂 𝑥 + 𝐴 𝑦 𝒂 𝑦 + 𝐴 𝑧 𝒂 𝑧 −∞ < 𝑥, 𝑦, 𝑧 < ∞ fralbe.com
- 16. Coordenadas Cilíndricas circulares(𝜌, 𝜙, 𝑧) 0 ≤ 𝜌 < ∞ 0 ≤ 𝜙 < 2𝜋 −∞ ≤ 𝑧 < ∞ 𝐴 𝜌 𝒂 𝜌 + 𝐴 𝜙 𝒂 𝜙 + 𝐴 𝑧 𝒂 𝑧 fralbe.com
- 17. Transformación de CoordenadasCilíndricas – Rectangulares 𝜌 = 𝑥2 + 𝑦2 𝜙 = tan−1 𝑦 𝑥 𝑧 = 𝑧 Rectangulares a Cilíndricas 𝑥 = 𝜌 cos 𝜙 𝑦 = 𝜌 sen 𝜙 𝑧 = 𝑧 Cilíndricas a Rectangulares fralbe.com
- 18. Coordenadas Esféricas (𝑟,𝜃, 𝜙) 0 ≤ 𝑟 < ∞ 0 ≤ 𝜃 < 𝜋 0 ≤ 𝜙 < 2𝜋 𝐴 𝑟 𝒂 𝑟 + 𝐴 𝜃 𝒂 𝜃 + 𝐴 𝜙 𝒂 𝜙 fralbe.com
- 19. Transformación Coordenadas Esféricas– Rectangulares 𝑟 = 𝑥2 + 𝑦2 + 𝑧2 𝜃 = tan−1 𝑥2 + 𝑦2 𝑧 𝜙 = tan−1 𝑦 𝑥 Rectangulares a Esféricas 𝑥 = 𝑟 sen 𝜃 cos 𝜙 𝑦 = 𝑟 sen 𝜃 sen 𝜙 𝑧 = 𝑟 cos 𝜃 Esféricas a Rectangulares fralbe.com
- 20.
- 21.
- 22.
- 23.
- 24. CÁLCULO APLICADO AVECTORES fralbe.com
- 25. C. Rectangulares Desplazamiento diferencial𝒅𝐥 = 𝑑𝑥 𝒂 𝑥 + 𝑑𝑦 𝒂 𝑦 + 𝑑𝑧 𝒂 𝑧 Área normal diferencial Volumen diferencial d𝐒 = 𝑑𝑦 𝑑𝑧 𝒂 𝑥 𝑑𝑥 𝑑𝑧 𝒂 𝑦 𝑑𝑥 𝑑𝑦 𝒂 𝑧 𝑑𝑣 = 𝑑𝑥 𝑑𝑦 𝑑𝑧 fralbe.com
- 26. C. Cilíndricas Desplazamiento diferencial𝒅𝐥 = 𝑑𝜌 𝒂 𝜌 + 𝜌 𝑑𝜙 𝒂 𝜙 + 𝑑𝑧 𝒂 𝑧 Área normal diferencial Volumen diferencial d𝐒 = 𝜌 𝑑𝜙 𝑑𝑧 𝒂 𝜌 𝑑𝜌 𝑑𝑧 𝒂 𝜙 ρ 𝑑𝜙 𝑑𝜌 𝒂 𝑧 𝑑𝑣 = 𝜌 𝑑𝜌 𝑑𝜙 𝑑𝑧 fralbe.com
- 27. C. Esféricas Desplazamiento diferencial𝒅𝐥 = 𝑑𝑟 𝒂 𝑟 + 𝑟 𝑑𝜃 𝒂 𝜃 + r sen θ 𝑑𝜙 𝒂 𝜙 Área normal diferencial Volumen diferencial d𝐒 = 𝑟2 sen 𝜃 𝑑𝜃 𝑑𝜙 𝒂 𝑟 r sen θ 𝑑𝑟 𝑑𝜙 𝒂 𝜃 r 𝑑𝑟 𝑑𝜃 𝒂 𝜙 𝑑𝑣 = 𝑟2 sen 𝜃 𝑑𝑟 𝑑𝜃 𝑑𝜙 fralbe.com
- 28. Integral de línea 𝑨∙ 𝑑𝐥𝐿 es la integral de la componente tangencial de 𝑨 a lo largo de la curva L. 𝑨 ∙ 𝑑𝐥 𝐿 = 𝑨 𝑐𝑜𝑠 𝜃 𝑑𝑙 𝑏 𝑎 A campo vectorial L curva fralbe.com
- 29. Integral de superficiey volumen Integral de superficie: 𝜓 = 𝑨 ∙ 𝑑𝑺 𝑆 Integral de volumen: 𝜌 𝑣 𝑑𝑣 𝑣 fralbe.com
- 30. Operador gradiente (𝛻) 𝛻= 𝜕 𝜕𝑥 𝒂 𝑥 + 𝜕 𝜕𝑦 𝒂 𝑦 + 𝜕 𝜕𝑧 𝒂 𝑧 Operador útil para definir: 1. El gradiente de un escarl V, el cual se escribe 𝛻𝑉. 2. La divergencia de un vector 𝑨, la cual se escribe 𝛻 ∙ 𝑨 3. El rotacional de un vector 𝑨, el cual se escribe 𝛻 × 𝑨 4. El laplaciano de un escalar 𝑉, el cual se escribe 𝛻2 𝑉. 𝛻 = 𝒂 𝜌 𝜕 𝜕𝜌 + 𝒂 𝜙 1 𝜌 𝜕 𝜕𝜙 + 𝒂 𝑧 𝜕 𝜕𝑧 C. cilíndricas: 𝛻 = 𝒂 𝑟 𝜕 𝜕𝑟 + 𝒂 𝜃 1 𝑟 𝜕 𝜕𝜃 + 𝒂 𝜙 1 𝑟 sen 𝜃 𝜕 𝜕𝜙 C. esféricas: fralbe.com
- 31. Gradiente de unEscalar El gradiente de un campo escalar 𝑉 es un vector que representa tanto la magnitud como la dirección de la máxima rapidez de incremento espacial de 𝑉. 𝛻𝑉 = 𝜕𝑉 𝜕𝑥 𝒂 𝑥 + 𝜕𝑉 𝜕𝑦 𝒂 𝑦 + 𝜕𝑉 𝜕𝑧 𝒂 𝑧C. rectangulares: 𝛻𝑉 = 𝒂 𝜌 𝜕𝑉 𝜕𝜌 + 𝒂 𝜙 1 𝜌 𝜕𝑉 𝜕𝜙 + 𝒂 𝑧 𝜕𝑉 𝜕𝑧 C. cilíndricas: 𝛻𝑉 = 𝒂 𝑟 𝜕𝑉 𝜕𝑟 + 𝒂 𝜃 1 𝑟 𝜕𝑉 𝜕𝜃 + 𝒂 𝜙 1 𝑟 sen 𝜃 𝜕𝑉 𝜕𝜙 C. esféricas: fralbe.com
- 32. Divergencia de unvector La divergencia de 𝑨 en un punto dado P es el flujo hacia fuera por unidad de volumen a medida que el volumen se contrae alrededor de P. 𝛻 ∙ 𝑨 = 𝜕𝐴 𝑥 𝜕𝑥 + 𝜕𝐴 𝑦 𝜕𝑦 + 𝜕𝐴 𝑧 𝜕𝑥 C. rectangulares: 𝛻 ∙ 𝑨 = 1 𝜌 𝜕 𝜕𝜌 (𝜌 𝐴 𝜌) + 1 𝜌 𝜕𝐴 𝜙 𝜕𝜙 + 𝒂 𝑧 𝜕𝐴 𝑧 𝜕𝑧 C. cilíndricas: 𝛻 ∙ 𝑨 = 1 𝑟2 𝜕 𝜕𝑟 (𝑟2 𝐴 𝑟) + 1 𝑟 sen 𝜃 𝜕 𝜕𝜃 (𝐴 𝜃 sen 𝜃) + 1 𝑟 sen 𝜃 𝜕𝐴 𝜙 𝜕𝜙 C. esféricas: fralbe.com
- 33. Teorema de laDivergencia El teorema de la divergencia establece que el flujo total hacia fuera de un campo vectorial 𝑨 a través de la superficie cerrada 𝑆 equivale a la integral de volumen de la divergencia de 𝑨. 𝑨 ∙ 𝑑𝑺 𝑆 = 𝛻 ∙ 𝑨 𝑣 𝑑𝑣 fralbe.com
- 34. Rotacional de unvector El rotacional de 𝑨 es un vector axial (o rotacional) cuya magnitud es la circulación máxima de 𝑨 por unidad de área conforme el área tiende a cero y cuya dirección es la dirección normal del área cuando el área se orienta de tal forma que de ello resulta la circulación máxima. 𝛻 × 𝑨 = 𝜕𝐴 𝑧 𝜕𝑦 − 𝜕𝐴 𝑦 𝜕𝑧 𝒂 𝑥 + 𝜕𝐴 𝑥 𝜕𝑧 − 𝜕𝐴 𝑧 𝜕𝑥 𝒂 𝑦 + 𝜕𝐴 𝑦 𝜕𝑥 − 𝜕𝐴 𝑥 𝜕𝑦 𝒂 𝑧 C. Rectangulares 𝛻 × 𝑨 = 1 𝜌 𝜕𝐴 𝑧 𝜕𝜙 − 𝜕𝐴 𝜙 𝜕𝑧 𝒂 𝜌 + 𝜕𝐴 𝜌 𝜕𝑧 − 𝜕𝐴 𝑧 𝜕𝜌 𝒂 𝜙 + 1 𝜌 𝜕(𝜌𝐴 𝜙) 𝜕𝜌 − 𝜕𝐴 𝜌 𝜕𝜙 𝒂 𝑧 C. Cilíndricas 𝛻 × 𝑨 = C. Esféricas fralbe.com
- 35. Teorema de Stokes Elteorema de Stokes establece que la circulación de un campo vectorial 𝑨 alrededor de una trayectoria (cerrada) 𝐿 es igual a la integral de superficie del rotacional de 𝑨 sobre la superficie abierta 𝑆 circunscrita por 𝐿, siempre que 𝑨 y 𝛻 × 𝑨 sean continuos en 𝑆. 𝑨 ∙ 𝑑𝐥 = (𝛻 × 𝑨) ∙ 𝑑𝑺 𝑆𝐿 fralbe.com
- 36. Laplaciano de unEscalar El laplaciano de un campo escalar 𝑉, el cual se escribe 𝛻2 𝑉, es la divergencia del gradiente de 𝑉. 𝛻2 𝑉 = 𝜕2 𝑉 𝜕𝑥2 𝒂 𝑥 + 𝜕2 𝑉 𝜕𝑦2 𝒂 𝑦 + 𝜕2 𝑉 𝜕𝑧2 𝒂 𝑧 C. rectangulares: fralbe.com
- 37. Referencias • SADIKU, MATTHEWN., Elementos de Electromagnetismo, 2010. fralbe.com
- 38. Esta obra estabajo licencia Creative Commons de Reconocimiento, No Comercial y Sin Obras Derivadas, Ecuador 3.0 www.creativecommons.org www.fralbe.com fralbe.com