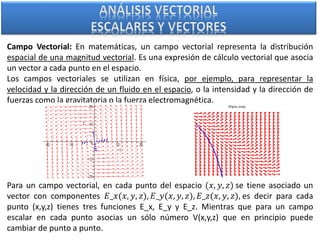
El documento describe diferentes tipos de magnitudes físicas y sistemas de coordenadas. Explica que un escalar se expresa por un solo número e indica la temperatura como un ejemplo. Un vector tiene magnitud, dirección y sentido, como la velocidad. Los campos escalares y vectoriales asocian valores a puntos en el espacio. También define sistemas de coordenadas cartesianas, polares, cilíndricas y esféricas. Finalmente, describe el producto escalar y vectorial entre vectores.

2. Escalar: Un escalar es un tipo de magnitud física que se expresa por un solo número
(positivo o negativo) y tiene el mismo valor para todos los observadores, y no posee
como tal una dirección física.
Por ejemplo, la temperatura de un cuerpo se expresa con una magnitud escalar. Una
magnitud física se denomina escalar cuando puede representarse con un único
número (única coordenada) invariable en cualquier sistema de referencia. Así la
masa de un cuerpo es un escalar, pues basta un número para representarla (por
ejemplo: 75 kg). Otros son la presión (más no la fuerza), el volumen, voltaje; o
cantidades globales tal como: la temperatura.
Vector: es una herramienta geométrica
utilizada para representar una magnitud física
definida por su módulo (o longitud), su
dirección (u orientación) y su sentido (que
distingue el origen del extremo). Ejemplo son
la velocidad, la aceleración, fuerza, etc.

3. Campo Escalar : En matemáticas y física, un campo escalar representa la distribución
espacial de una magnitud escalar, asociando un valor a cada punto del espacio. En
matemáticas, el valor es un número; en física, una magnitud física. Los campos
escalares se usan en física, por ejemplo, para indicar la distribución de la
temperatura o la presión de un gas en el espacio.
Un campo escalar en cada punto asocias un sólo número V(x,y,z) que en principio
puede cambiar de punto a punto.

4. Campo Vectorial: En matemáticas, un campo vectorial representa la distribución
espacial de una magnitud vectorial. Es una expresión de cálculo vectorial que asocia
un vector a cada punto en el espacio.
Los campos vectoriales se utilizan en física, por ejemplo, para representar la
velocidad y la dirección de un fluido en el espacio, o la intensidad y la dirección de
fuerzas como la gravitatoria o la fuerza electromagnética.
Para un campo vectorial, en cada punto del espacio (𝑥, 𝑦, 𝑧) se tiene asociado un
vector con componentes 𝐸_𝑥(𝑥, 𝑦, 𝑧), 𝐸_𝑦(𝑥, 𝑦, 𝑧), 𝐸_𝑧(𝑥, 𝑦, 𝑧), es decir para cada
punto (x,y,z) tienes tres funciones E_x, E_y y E_z. Mientras que para un campo
escalar en cada punto asocias un sólo número V(x,y,z) que en principio puede
cambiar de punto a punto.

5. Campo Vectorial:
Líneas de fuerza: los campos vectoriales se representan por líneas continuas con
orientación de los vectores de campo sobre una región definida. Estas líneas reciben
el nombre de líneas de fuerza.
Las líneas de fuerza cumplen con las
siguientes propiedades:
• Los vectores de campo en cualquier
punto son siempre tangenciales a la línea
de fuerza que pasa por el punto dado.
• Las líneas de fuerza no se cruzan en
ningún punto aunque pueden seguir
trayectorias cerradas.
• La cantidad de líneas de fuerza en
cualquier porción del espacio en que se
encuentra definido el campo es
proporcional a la intensidad del campo
vectorial.

6. Sistema de coordenadas cartesianas: un sistema de coordenadas cartesianas se
define por dos o tres ejes ortogonales igualmente escalados, dependiendo de si es
un sistema bidimensional o tridimensional. El valor de cada una de las coordenadas
de un punto (A) es igual a la proyección ortogonal del vector de posición de dicho
punto
𝑓 𝑥, 𝑦, 𝑧
𝑟 = 𝑥2 + 𝑦2 + 𝑧2
𝑑𝐿 = 𝑑𝑥 ∙ 𝑎 𝑥 + 𝑑𝑦 ∙ 𝑎 𝑦 + 𝑑𝑧 ∙ 𝑎 𝑧
𝑑𝑆 𝑧 = 𝑑𝑥 ∙ 𝑑𝑦 ∙ 𝑎 𝑧
𝑑𝑆 𝑦 = 𝑑𝑥 ∙ 𝑑𝑧 ∙ 𝑎 𝑦
𝑑𝑆 𝑥 = 𝑑𝑦 ∙ 𝑑𝑧 ∙ 𝑎 𝑥
𝑑𝑉 = 𝑑𝑥 ∙ 𝑑𝑦 ∙ 𝑑𝑧

7. Sistema de coordenadas polares:
Es un sistema de coordenadas bidimensional en el cual cada punto del plano se
determina por un ángulo y una distancia.
𝑥 = 𝜌 ∙ 𝑐𝑜𝑠 ∅
𝑦 = 𝜌 ∙ 𝑠𝑒𝑛𝑜 ∅
𝜌∅
Sistema de coordenadas cilíndricas
Las coordenadas cilíndricas son un sistema de coordenadas para definir la posición de un punto
del espacio mediante un ángulo, una distancia con respecto a un eje y una altura en la dirección
del eje.
El sistema de coordenadas cilíndricas es muy conveniente en aquellos casos en que se tratan
problemas que tienen simetría de tipo cilíndrico o acimutal. Se trata de una versión en tres
dimensiones de las coordenadas polares de la geometría analítica plana.
𝑧 = 𝑧
𝑟 = 𝜌2 + 𝑧2
𝑑𝐿 = 𝑑𝜌 ∙ 𝑎 𝜌 + 𝜌 ∙ 𝑑∅ ∙ 𝑎∅ + 𝑑𝑧 ∙ 𝑎 𝑧
𝑑𝑆 𝑧 = 𝜌 ∙ 𝑑∅ ∙ 𝑑𝜌 ∙ 𝑎 𝑧
𝑑𝑆 𝜌 = 𝜌 ∙ 𝑑∅ ∙ 𝑑𝑧 ∙ 𝑎 𝜌
𝑑𝑆∅ = 𝑑𝜌 ∙ 𝑑𝑧 ∙ 𝑎∅
𝑑𝑉 = 𝜌 ∙ 𝑑∅ ∙ 𝑑𝜌 ∙ 𝑑𝑧

8. Sistema de coordenadas esféricas
El sistema de coordenadas esféricas se basa en la misma idea que las coordenadas
polares y se utiliza para determinar la posición espacial de un punto mediante una
distancia y dos ángulos.
En consecuencia, un punto P queda representado por un conjunto de tres magnitudes:
el radio r, el ángulo polar o colatitud θ y el azimut φ.
𝑥 = 𝑟 ∙ 𝑠𝑒𝑛𝑜(𝜃) ∙ 𝑐𝑜𝑠 ∅
𝑦 = 𝑟 ∙ 𝑠𝑒𝑛𝑜(𝜃) ∙ 𝑠𝑒𝑛𝑜 ∅
𝑧 = 𝑟 ∙ 𝑐𝑜𝑠(𝜃)
𝑑𝐿 = 𝑑𝑟 ∙ 𝑎 𝑟 + 𝑟 ∙ 𝑑𝜃 ∙ 𝑎 𝜃 + 𝑟 ∙ 𝑠𝑒𝑛𝑜(𝜃) ∙ 𝑑∅ ∙ 𝑎∅
𝑑𝑆∅ = 𝑟 ∙ 𝑑𝜃 ∙ 𝑑𝑟 ∙ 𝑎∅
𝑑𝑆 𝜌 = 𝑟 ∙ 𝑠𝑒𝑛𝑜(𝜃) ∙ 𝑑∅ ∙ 𝑑𝑟 ∙ 𝑎 𝜃
𝑑𝑆 𝑟 = 𝑟2
∙ 𝑠𝑒𝑛𝑜(𝜃) ∙ 𝑑∅ ∙ 𝑑𝜃 ∙ 𝑎 𝑟
𝑑𝑉 = 𝑟2
∙ 𝑠𝑒𝑛𝑜(𝜃) ∙ 𝑑𝜃 ∙ 𝑑∅ ∙ 𝑑𝑟

9. Producto Escalar (Punto): En matemática, el producto escalar, también conocido
como producto interno, producto interior o producto punto, es una operación entre
dos vectores de un mismo espacio. El resultado de esta operación es un número o
escalar que resulta de sumar las multiplicaciones de las dimensiones de estos dos
vectores en cada uno de los ejes coordenados.
𝐴 = 𝑎 𝑥, 𝑎 𝑦, 𝑎 𝑧 B = 𝑏 𝑥, 𝑏 𝑦, 𝑏 𝑧
𝐴 ∗ 𝐵 = 𝐴 ∙ 𝐵 ∙ 𝑐𝑜𝑠 𝜃𝐴𝐵
𝐴 ∗ 𝐵 = 𝑎 𝑥 ∙ 𝑏 𝑥 + 𝑎 𝑦 ∙ 𝑏 𝑦 + 𝑎 𝑧 ∙ 𝑏 𝑧
Esta operación permite explotar los conceptos de la geometría euclídea tradicional:
longitudes, ángulos, ortogonalidad en dos y tres dimensiones. El producto escalar
puede definirse también en los espacios euclídeos de dimensión mayor a tres, y en
general en los espacios vectoriales reales y complejos. Los espacios vectoriales
dotados de producto escalar reciben el nombre de espacios prehilbertianos.

10. Propiedades Producto Punto
𝐴 ∗ 𝐴 = 𝐴 2
𝐴 ∗ 𝐵 + 𝐶 = 𝐴 ∗ 𝐵 + 𝐴 ∗ 𝐶
𝐴 ∗ 𝐵 = 𝐵 ∗ 𝐴 𝑐 ∙ 𝐴 ∗ 𝐵 = 𝑐 ∙ 𝐵 ∗ 𝐴 = 𝐴 ∗ 𝑐 ∙ 𝐵
0 ∗ 𝐴 = 0
Teorema:
𝐴 ∗ 𝐵 = 𝐴 ∙ 𝐵 ∙ 𝑐𝑜𝑠 𝜃𝐴𝐵
𝐴 ∗ 𝐵 > 0 entonces 𝜃𝐴𝐵 es agudo
𝐴 ∗ 𝐵 < 0 entonces 𝜃𝐴𝐵 es Obtuso
𝐴 ∗ 𝐵 = 0 entonces 𝜃𝐴𝐵 =
𝜋
2
𝐴 ∗ 𝐵 = 𝐴 ∙ 𝐵 entonces 𝜃𝐴𝐵 = 0

11. La aplicación más común del producto punto se halla en el área mecánica, donde si
se aplica una fuerza constante 𝐹, y esta produce un desplazamiento 𝐿, el trabajo
realizado se define como:
𝐹 ∗ 𝐿 = 𝐹 ∙ 𝐿 ∙ 𝑐𝑜𝑠 𝜃
Si se supone que la fuerza varia a lo largo de una trayectoria, es necesario hallar la
integral a lo largo de esa trayectoria.
𝑇𝑟𝑎𝑏𝑎𝑗𝑜 = න 𝐹 ∗ 𝑑𝐿
Otro ejemplo clásico se halla en los campos magnéticos.

12. Producto Cruz (Vectorial): En Matemáticas, el producto cruz, producto vectorial, o
producto vectorial de Gibbs es una operación binaria entre dos vectores en un
espacio tridimensional. El resultado es un vector perpendicular a los vectores que
se multiplican, y por lo tanto normal al plano que los contiene. Debido a su
capacidad de obtener un vector perpendicular a otros dos vectores, cuyo sentido
varía de acuerdo al ángulo formado entre estos dos vectores, esta operación es
aplicada con frecuencia para resolver problemas matemáticos, físicos o de
ingeniería.
𝐴 = 𝑎 𝑥, 𝑎 𝑦, 𝑎 𝑧 B = 𝑏 𝑥, 𝑏 𝑦, 𝑏 𝑧
𝐴 𝑥 𝐵 = 𝐴 ∙ 𝐵 ∙ 𝑠𝑒𝑛𝑜 𝜃𝐴𝐵 𝑘
𝐴 𝑥 𝐵 =
𝑖 𝑗 𝑘
𝑎 𝑥 𝑎 𝑦 𝑎 𝑧
𝑏 𝑥 𝑏 𝑦 𝑏 𝑧
= 𝑎 𝑦 ∙ 𝑏 𝑧 − 𝑎 𝑧 ∙ 𝑏 𝑦 ∙ 𝑖 − 𝑎 𝑥 ∙ 𝑏 𝑧 − 𝑎 𝑧 ∙ 𝑏 𝑥 ∙ 𝑗
+ 𝑎 𝑥 ∙ 𝑏 𝑦 − 𝑎 𝑦 ∙ 𝑏 𝑥 ∙ 𝑘

13. Propiedades Producto Cruz
𝐴 𝑥 𝐴 = 0 𝐴 𝑥 𝐵 + 𝐶 = 𝐴 𝑥 𝐵 + 𝐴 𝑥 𝐶
𝐴 𝑥 𝐵 = − 𝐵 𝑥 𝐴 𝑐 ∙ 𝐴 𝑥 𝐵 = 𝑐 ∙ 𝐵 𝑥 𝐴 = 𝐴 𝑥 𝑐 ∙ 𝐵
0 𝑥 𝐴 = 𝐴 𝑥 0 = 0 𝐴 𝑥 𝐴 + 𝐵 = 0
Teorema:
𝐴 = 𝑎 𝑥, 𝑎 𝑦, 𝑎 𝑧 B = 𝑏 𝑥, 𝑏 𝑦, 𝑏 𝑧
𝐴 𝑥 𝐵 = 𝐴 ∙ 𝐵 ∙ 𝑠𝑒𝑛𝑜 𝜃𝐴𝐵 𝑘
Si 𝐴 𝑥 𝐵 = 0 y 𝐴, 𝐵 ≠ 0 Entonces 𝜃𝐴𝐵 = 0°