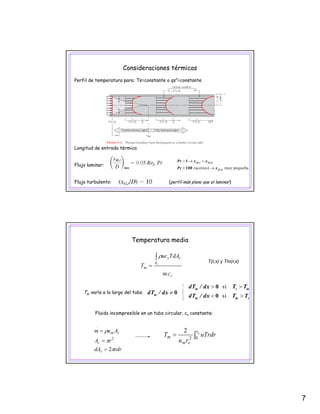
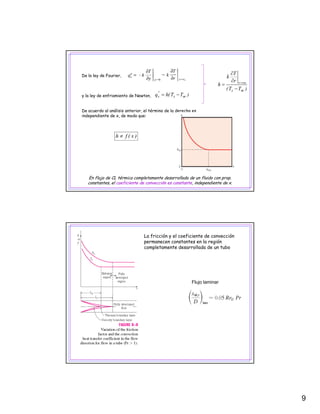
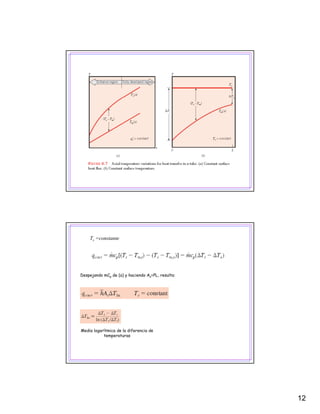
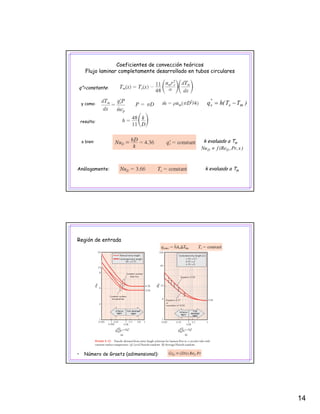
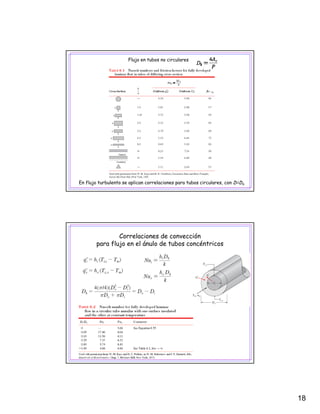
El documento describe los conceptos fundamentales de la convección forzada en flujo interno, incluyendo consideraciones hidrodinámicas y térmicas. Explica que en la región completamente desarrollada, la velocidad, presión, temperatura y coeficiente de convección se mantienen constantes a lo largo del tubo. También presenta correlaciones para calcular el número de Nusselt en flujos laminar y turbulento.

1. 1
Unidad 8.
Convección forzada, flujo interno
• Consideraciones hidrodinámicas:
– longitud de entrada hidrodinámica velocidad media y CL delongitud de entrada hidrodinámica, velocidad media y CL de
velocidad completamente desarrollada
– caída de presión, factor de fricción y coeficiente de fricción
• Consideraciones térmicas:
– longitud de entrada térmica, temperatura media y CL térmica
completamente desarrollada
• Balance de energía:
– flujo de calor constante
– temperatura constante
• Correlaciones de convección para flujo laminar y turbulento en tubos
circulares, no circulares y concéntrico
Consideraciones hidrodinámicas
• Región de entrada: u(r,x)
• Región completamente desarrollada: u(r), parabólico (flujo laminar) o
ámás plano (flujo turbulento)
υ
Du
ReRe m
Dc,D =≈ 2300
• La extensión de la región de entrada varía si el flujo es laminar o
turbulento
• Reynolds crítico:

2. 2
Longitud de entrada hidrodinámica
x
⎟
⎞
⎜
⎛
2300≤DReD
lam
hfd
D
x
Re.
,
050≈⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
6010 ≤⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
≤
turb
hfd
D
x ,
Flujo turbulento
completamente
desarrollado: x/D>10
(perfil más plano que en(perfil más plano que en
régimen laminar)
Velocidad media
Como la velocidad varía sobre la sección transversal del tubo, se define una
velocidad media de la ecuación de continuidad:
Para flujo incompresible y ro=D/2:
∫∫ == oo rr
rdr)xr(urdr)xr(uu
22πρ
cm
A
c
.
AudA)x,r(um
c
ρρ == ∫ μπD
m
Re
.
D
4
=
∫∫
oo
m rdr)x,r(u
r
rdr)x,r(u
r
u 0202
ρπ

3. 3
Flujo laminar,
incompresible,
propiedades constantes ,
tubo circular
u0
Perfil de Velocidad en la región completamente
desarrollada
tubo circular
Característica en región completamente desarrollada:
v=0 y du/dx=0 ⇒ u(r,x)=u(r)
Para el elemento anular diferencial
• Integrando 2 veces

4. 4
• Perfil de velocidad parabólico
→= ∫
or
o
m rdr)x,r(u
r
u 02
2
mo uuur 20 ==→=
uo
2
D
dx
dp
f
⎟
⎠
⎞
⎜
⎝
⎛−
=
Factor de fricción
de Moody (o Darcy)
Caída de presión y factor de fricción en flujo
completamente desarrollado en tubos circulares
2
2
muρ
2
2
m
s
f
u
C
ρ
τ
=
de Moody (o Darcy)
Coeficiente de fricción
de Fanning
4
f
C f =
orr
s
dr
du
=
⎟
⎠
⎞
⎜
⎝
⎛
−= μτComo: derivando el perfil de velocidad, resulta:

5. 5
Expresiones analíticas del factor de fricción
tubos circulares
Se obtiene una expresión analítica reemplazando um y ReD,
en la expresión de f:
64
Flujo laminar:
2
D
f
Re
=
64
( )dx/dp
r
u o
m
μ8
2
−=
Flujo turbulento, tubos lisos: datos experimentales correlacionados (Diagrama de Moody)
ReD<2 .104
/
D
.
f
Re
= 1 4
0 316
/
D
.
f
Re
= 1 5
0 184
ReD>2.104
O bien, la correlación de Petukhov:
Expresiones analíticas del factor de fricción
tubos circulares
La correlación de Colebrook, permite calcular el factor de fricción
para flujo turbulento en función de la rugosidad de la superficie
d l t bdel tubo, e:
Las correlaciones anteriores se grafican en el Diagrama de Moody.
En flujo completamente desarrollado: f y dp/dx son constantes,
de modo que integrando su definición puede hallarse la caída de
( )
m
dp D
dx
f
uρ
−
= 2
2 .
m
V.pPotencia
)xx(
D
u
fp
Δ=
−=Δ 12
2
2
ρIntegrando:
de modo que integrando su definición, puede hallarse la caída de
presión en dirección axial

6. 6
• De la ecuación de Colebrook
Tubos circulares, flujo completamente desarrollado

7. 7
Perfil de temperatura para: Ts=constante o qs”=constante
Consideraciones térmicas
Longitud de entrada térmica
Flujo laminar:
Flujo turbulento: (perfil más plano que el laminar)
(aceites) muy pequeña
fd ,t fd ,h
fd ,h
Pr x x
Pr x
> → >
≥ →
1
100
Temperatura media
c
A
v
m
dATuc
T c
∫
=
ρ
T(r,x) y Tm(r,x)
v
.
cm
Fluido incompresible en un tubo circular, cv constante:
Tm varía a lo largo del tubo mdT / dx ≠ 0
si
si
m s m
m m s
dT / dx T T
dT / dx T T
> >
< >
0
0
rdrdA
rA
Aum
c
c
cm
.
π
π
ρ
2
2
=
=
=
∫= or
om
m uTrdr
ru
T 02
2

8. 8
Flujo de calor local, flujo interno
)TT(h"q msx −= )TT(hq msx
donde:
h: coef. conv. local
Ts : temp. de la superficie
Tm: temperatura media del fluido (f(x))
Condiciones de flujo completamente desarrollado en CL
térmica
rdx/dTydx/dT
dx/du
m ∀≠≠
=
00
0
T(r) varía con x, pero cuando el flujo está completamente desarrollado,
la forma relativa del perfil no cambia, o sea:
0=⎥
⎦
⎤
⎢
⎣
⎡
−
−
∂
∂
t,fdms
s
)x(T)x(T
)x,r(T)x(T
x
y también su derivada respecto a r debe ser independiente de x:
→ independiente de x
Estas ecuaciones se aplican para las 2 posibles condiciones de superficie
q”= constante (Ts=Ts(x)) o Ts constante

9. 9
De la ley de Fourier,
y la ley de enfriamiento de Newton, )TT(hq ms
"
s −=
)TT(
r
T
k
h
ms
ror
−
∂
∂
= =
y y ,
De acuerdo al análisis anterior, el término de la derecha es
independiente de x, de modo que:
)x(fh ≠
mss
En flujo de CL térmica completamente desarrollada de un fluido con prop.
constantes, el coeficiente de convección es constante, independiente de x.
La fricción y el coeficiente de convección
permanecen constantes en la región
completamente desarrollada de un tubo
Flujo laminar

10. 10
Balance de energía
Consideraciones generales
q dhδ →
Flujo en un tubo: SARE,
despreciamos Ec y Ep
. .
conv p m ,s m ,e
q dh
q m c (T T )
δ = →
= −
Expresión general, independiente de la naturaleza de la
superficie térmica o condiciones de flujo en el tubo
PdxqdTcmdq "
smp
.
conv ==
p
.
"
sm
cm
Pq
dx
dT
=
Válida para las 2 condiciones de superficie:
• flujo de calor constante en la pared del
tubo
• temperatura de pared constante
P=πD
q”s =constanteFlujo de calor constante en la pared del tubo
PLqq "
sconv =
constante
cm
Pq
dx
dT
p
.
"
sm
==
x
cm
Pq
T)x(T
p
.
"
s
e,mm +=
h
q
)x(Tm)x(Ts)TT(hq
"
s
ms
"
s +=⇒−=
Si q” no es constante, pero es una función conocida de x, las expresiones anteriores
tienen solución

11. 11
h
q
)x(Tm)x(Ts
"
s
+=
Derivando la expresión para la región (térmica) completamente
desarrollada :
t,fd
m
t,fd
s
dx
dT
dx
dT
=
y del perfil adimensional de T:
Por lo tanto:
constante
cm
Pq
dx
dT
dx
dT
dx
dT
p
.
"
s
t,fd
m
t,fd
s
t,fd
====
Ts =constanteTemperatura constante en la pared del tubo
p
.
"
sm
cm
Pq
dx
dT
= )TT(hq ms
"
s −=
ms TTT −=Δ
(a)Integrando entre la entrada y la salida del tubo:
Integrando entre la entrada y una posición axial x del tubo:

12. 12
Ts =constante
Despejando mCp de (a) y haciendo As=PL, resulta:
Media logarítmica de la diferencia de
temperaturas

13. 13
Las expresiones anteriores pueden aplicarse si en lugar de Ts, se conoce la
temperatura de un fluido externo T∞:
O bien:
: coeficiente promedio global de transferencia de
calor y Rtot: resistencia total al flujo de calor
U
R
AUAUAU
tot
ooiis
1
=== ( ) ( ) ( )ooiioii
i
hr/rr/rlnk/rh/
U
++
=
1
1
AR
U
tot
1
=
Coeficientes de convección teóricos
Flujo laminar completamente desarrollado en tubos circulares
A partir de la ecuación de la capa límite térmica y de las aproximaciones de CL,
reemplazando el perfil de velocidades encontramos el perfil de temperaturas para
flujo de calor constante:
2
⎥
⎤
⎢
⎡
⎟
⎞
⎜
⎛ r)r(u
0
12
=
⎥
⎥
⎦
⎢
⎢
⎣
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
υ
om r
r
u
)r(u
mud dT r dT
r
r dr dr r dxα
⎡ ⎤⎛ ⎞⎛ ⎞ ⎛ ⎞
⎢ ⎥= −⎜ ⎟⎜ ⎟ ⎜ ⎟
⎝ ⎠ ⎝ ⎠⎢ ⎥⎝ ⎠⎣ ⎦
2
0
21
1
q”=ctte.:
Perfil de u
q
Perfil de T
Reemplazando ambos perfiles en : ∫= or
om
m uTrdr
ru
T 02
2

14. 14
Coeficientes de convección teóricos
Flujo laminar completamente desarrollado en tubos circulares
q”=constante:
)TT(hq ms
"
s −=y como:
resulta:
o bien: k evaluado a Tm
)xPr,,(RefNu DD ≠
k evaluado a TmAnálogamente:
Región de entrada
• Número de Graetz (adimensional):

15. 15
Correlaciones que incluyen la región de entrada
Flujo laminar
• Correlación de Hausen (1943)
» (8.57)
• Correlación de Baehr y Stephan (2006)
• (8.58)
Si la temperatura media del fluido difiere mucho de la temperatura de
superficie, la siguiente corrección es necesaria (especialmente para
líquidos):
donde todas las propiedades son evaluadas a Tm excepto μs que se evalúa
a Ts

16. 16
Correlaciones de convección para flujo turbulento en
tubos circulares
• Ecuación de Dittus-Boelter (flujo turbulento completamente
desarrollado en u y T, tubos circulares lisos)
error~25%
Propiedades evaluadas a Tm
Correlaciones de convección para flujo turbulento en
tubos circulares
• Ecuación de Sieder y Tate (flujo turbulento completamente desarrollado
en u y T, tubos circulares lisos)
error~25%
propiedades evaluadas a Tm excepto μs que se evalúa a Ts
• La ecuaciones de Dittus-Bolter y Sieder y Tate pueden aplicarse a las
dos condiciones de superficie: temperatura constante y flujo de calor
constante

17. 17
Ecuación de Gnielinski (2300< ReD<5 106, 0.5<Pr<2000):
• Propiedades evaluadas a Tm
• Aplicable para ambas condiciones: q” constante y Ts constante
( )( )
( ) ( )187121
10008
3221
−+
−
= //
D
D
Pr/f.
PrRe/f
Nu ( ) 2
641790 −
−= .Reln.f Derror~10%
Tubos lisos
f puede obtenerse también del Diagrama de Moody
Metales líquidos,
flujo completamente desarrollado en tubos circulares lisos
Skupinski et al., 1965p ,
Seban y Shimazaki, 1951
Pe=Re Pr

18. 18
Flujo en tubos no circulares
En flujo turbulento se aplican correlaciones para tubos circulares, con D=Dh
Correlaciones de convección
para flujo en el ánulo de tubos concéntricos

19. 19
Flujo turbulento
• En flujo turbulento los coeficientes de convección interior y exterior son
aproximadamente iguales entre si y el ánulo del tubo puede considerarse
t b i l d diá t D D Dcomo un tubo circular de diámetro Dh=Do-Di
• Por lo tanto, el Nu puede calcularse con la Ecs. de Gnielinski vista
anteriormente para flujo turbulento y luego se corrige multiplicando por
los siguientes factores de corrección dados por Petukhov y Roizen (1964)

20. 20
Ejemplo
1. Flujo laminar o turbulento (propiedades a Tm) ?
2. Región CD o debe incluirse la región de entrada ?

21. 21
Ejemplo
1. Flujo laminar o turbulento (propiedades a Tm) ?
2. Región CD o debe incluirse la región de entrada ?