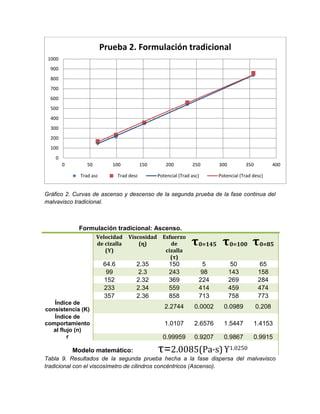
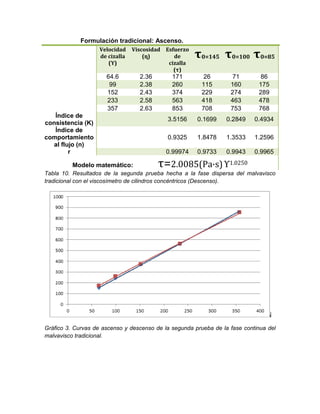
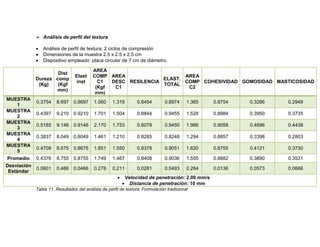
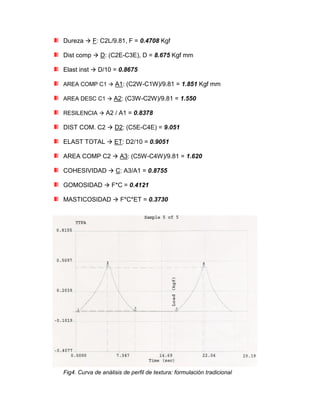
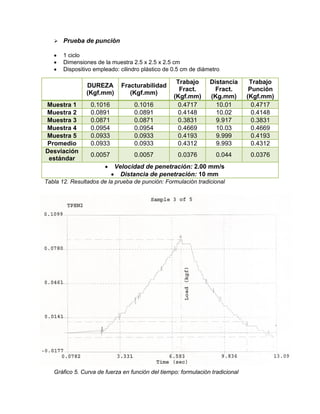
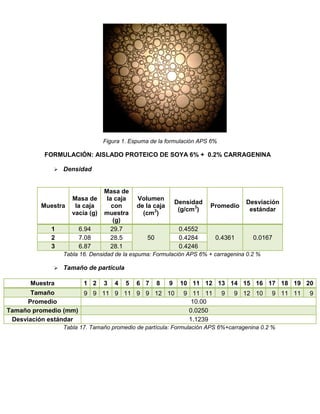
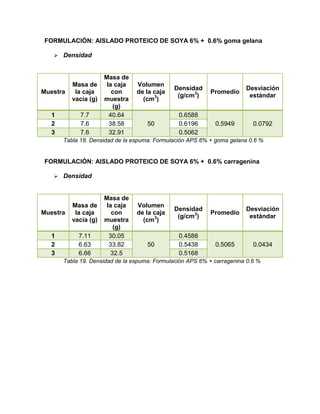
El informe detalla la elaboración y evaluación de malvaviscos utilizando goma gelana y carragenina como gelificantes, además de un aislado proteico de soya. Se realizaron pruebas reológicas, texturales y de estabilidad para determinar las propiedades funcionales de las formulaciones. Los resultados indican un buen rendimiento y estabilidad en la formulación tradicional, junto con análisis de textura y comportamiento reológico que se detallan a lo largo del documento.

1. UNIVERSIDAD NACIONAL AUTÓNOMA
DE MÉXICO
FACULTAD DE ESTUDIOS SUPERIORES CUAUTITLÁN
INGENIERÍA EN ALIMENTOS
LABORATORIO EXPERIMENTAL
MULTIDISCIPLINARIO I
GELES: ELABORACIÓN DE MALVAVISCOS
1ER INFORME DE RESULTADOS
Elaborado por:
 Cruz Tenjhay Karina
 Melo Cruz Stephanie
 Pérez Márquez Aline Jazmín
 Rincón Vázquez Ariadna Marina
Grupo: 2402
Profesoras:
Miriam Edith Fuentes Romero
Patricia Muñoz Aguilar
Cuautitlán Izcalli, Edo. de México; 27 de abril de 2015

2. GELES: ELABORACIÓN DE MALVAVISCOS
1er INFORME DE RESULTADOS
Para evaluar las propiedades funcionales de la goma gelana de alto acilo y
carragenina iota como agentes gelificantes y la propiedad espumante del aislado
proteico de soya (APS) en la elaboración de malvaviscos, se procedió a realizar
una serie de actividades y pruebas reológicas, texturales, de estabilidad y físicas.
FORMULACIÓN TRADICIONAL
La primera actividad fue la elaboración de malvaviscos de la forma tradicional,
cuyos resultados de las pruebas se muestran a continuación:
 Prueba de rendimiento
Formulación
Volumen
inicial
(mL)
Volumen
final
(mL)
Rendimiento
(%)
Promedio
Desviación
estándar
Tradicional
370 900 143.2432
143.6937 0.7802370 905 144.5946
370 900 143.2432
Tabla 1. Rendimiento de la espuma: Formulación tradicional
Para determinar el porcentaje de rendimiento se emplea la siguiente ecuación:
Donde: A: Volumen de la espuma (mL)
B: Volumen de la solución inicial (mL)
 Prueba de estabilidad
Formulación
Volumen
de la
mezcla
(mL)
Volumen
de
drenado
(mL)
Rendimiento
(%)
Promedio
Desviación
estándar
Tradicional
80 0 100.0000
100.0000 0.000080 0 100.0000
80 0 100.0000
Tabla 2. Estabilidad de la espuma: Formulación tradicional

3. Para determinar el porcentaje de estabilidad se emplea la siguiente ecuación:
Donde: A: Volumen de la mezcla (mL)
C: Volumen del drenado (mL)
 Densidad
Muestra
Masa de
la caja
vacía (g)
Masa de
la caja
con
muestra
(g)
Volumen
de la caja
(cm3
)
Densidad
(g/cm3
)
Promedio
Desviación
estándar
1 8.8 23.83
50
0.3006
0.2943 0.00782 8.26 23.09 0.2966
3 7.78 22.06 0.2856
Tabla 3. Densidad de la espuma: Formulación tradicional
Para determinar la densidad se emplea la siguiente ecuación:
Donde: D: Masa de la caja con muestra (g)
E: Masa de la caja vacía (g)
F: Volumen de la caja (cm3
)
 Tamaño de partícula
Muestra 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Tamaño 8 7 8 8 7 7 8 8 8 8 9 8 9 8 7 8 8 7 7 8
Promedio 7.8
Tamaño promedio (mm) 0.0195
Desviación estándar 0.6156
Tabla 4. Tamaño promedio de partícula: Formulación tradicional
El tamaño promedio se calcula multiplicando el primer promedio obtenido por la
medida de la división correspondiente al objetivo del microscopio empleado en la
experimentación.
Para este caso, se empleó el de 40x cuya división equivale a 0.0025 mm.

4. Figura 1. Espuma de la formulación tradicional
 Caracterización reológica
Se realizó una caracterización reológica, con el viscosímetro de cilindros
concéntricos, para determinar el tipo de fluido de la fase continua de los
malvaviscos, con los resultados obtenidos y una vez analizados, se llegó a la
conclusión de que se trata de un fluido adelgazante a la cizalla y utilizando el
modelo Herschel-Bulkley se planteó el modelo matemático.
Formulación tradicional: Ascenso.
Velocidad
de cizalla
()
Viscosidad
(ɳ)
Esfuerzo
de cizalla
()
0=145 0=100 0=85
64.6 2.36 152 7 52 67
99 2.32 230 85 130 145
152 2.34 356 211 256 271
233 2.36 551 406 451 466
357 2.36 843 698 743 758
Índice de
consistencia (Κ)
2.2811 0.0004 0.10008 0.2098
Índice de
comportamiento
al flujo (n)
1.0058 2.519 1.535 1.4081
r 0.99996 0.941 0.992 0.9957
Modelo matemático: =2.2811(Pa·s) 1.0058
Tabla 5. Resultados de la primer prueba hecha a la fase continua del malvavisco
tradicional con el viscosímetro de cilindros concéntricos (Ascenso).

5. Formulación tradicional: Descenso.
Velocidad
de cizalla
()
Viscosidad
(ɳ)
Esfuerzo
de
cizalla
()
0=145 0=100 0=85
64.6 2.35 169 24 69 84
99 2.40 252 107 152 167
152 2.46 373 228 273 288
233 2.55 559 414 459 474
357 2.72 839 694 739 754
Índice de
consistencia (Κ)
1.6463 0.0132 0.2590 0.4567
Índice de
comportamiento
al flujo (n)
0.0825 1.8905 1.3678 1.2707
r 0.9709 0.9730 0.9946 0.9968
Modelo matemático: τ=85(Pa)+2.2811(Pa·s)ϒ1.2707
Tabla 6. Resultados de la primer prueba hecha a la fase continua del malvavisco
tradicional con el viscosímetro de cilindros concéntricos (Descenso).
Gráfico 1. Curvas de ascenso y descenso de la primera prueba de la fase continua del
malvavisco tradicional.
0
100
200
300
400
500
600
700
800
900
0 50 100 150 200 250 300 350 400
Prueba 1. Formulación tradicional
Ascenso Descenso

6. Formulación tradicional: Ascenso.
Velocidad
de cizalla
(ϒ)
Viscosidad
(ɳ)
Esfuerzo
de
cizalla
(τ)
τ0=145 τ0=100 τ0=85
64.6 2.37 148 3 48 63
99 2.34 214 69 114 129
152 2.34 350 205 250 265
233 2.39 543 398 443 458
357 2.40 838 693 738 753
Índice de
consistencia (Κ)
2.0085 0.00003 0.704 0.1568
Índice de
comportamiento
al flujo (n)
1.0250 2.9562 1.59608 1.4571
r 0.99930 0.9266 0.934 0.9964
Modelo matemático: τ=2.0085(Pa·s)ϒ1.0250
Tabla 7. Resultados de la segunda prueba hecha a la fase dispersa del malvavisco
tradicional con el viscosímetro de cilindros concéntricos (Ascenso).
Formulación tradicional: Descenso.
Velocidad
de cizalla
(ϒ)
Viscosidad
(ɳ)
Esfuerzo
de
cizalla
(τ)
τ0=145 τ0=100 τ0=85
64.6 2.36 169 24 69 84
99 2.40 234 89 134 149
152 2.41 357 212 257 272
233 2.50 561 416 461 476
357 2.56 858 713 758 773
Índice de
consistencia (Κ)
2.8975 0.0094 0.2028 0.3643
Índice de
comportamiento
al flujo (n)
0.9646 1.9474 1.4102 1.31
r 0.99845 0.9841 0.9983 0.9993
Modelo matemático: τ=85(PA)+0.3643(Pa·s) ϒ1.31
Tabla 8. Resultados de la segunda prueba hecha a la fase dispersa del malvavisco
tradicional con el viscosímetro de cilindros concéntricos (Descenso).

7. Gráfico 2. Curvas de ascenso y descenso de la segunda prueba de la fase continua del
malvavisco tradicional.
Formulación tradicional: Ascenso.
Velocidad
de cizalla
(ϒ)
Viscosidad
(ɳ)
Esfuerzo
de
cizalla
(τ)
τ0=145 τ0=100 τ0=85
64.6 2.35 150 5 50 65
99 2.3 243 98 143 158
152 2.32 369 224 269 284
233 2.34 559 414 459 474
357 2.36 858 713 758 773
Índice de
consistencia (Κ) 2.2744 0.0002 0.0989 0.208
Índice de
comportamiento
al flujo (n)
1.0107 2.6576 1.5447 1.4153
r 0.99959 0.9207 0.9867 0.9915
Modelo matemático: τ=2.0085(Pa·s)ϒ1.0250
Tabla 9. Resultados de la segunda prueba hecha a la fase dispersa del malvavisco
tradicional con el viscosímetro de cilindros concéntricos (Ascenso).
0
100
200
300
400
500
600
700
800
900
1000
0 50 100 150 200 250 300 350 400
Prueba 2. Formulación tradicional
Trad asc Trad desc Potencial (Trad asc) Potencial (Trad desc)

8. Formulación tradicional: Ascenso.
Velocidad
de cizalla
(ϒ)
Viscosidad
(ɳ)
Esfuerzo
de
cizalla
(τ)
τ0=145 τ0=100 τ0=85
64.6 2.36 171 26 71 86
99 2.38 260 115 160 175
152 2.43 374 229 274 289
233 2.58 563 418 463 478
357 2.63 853 708 753 768
Índice de
consistencia (Κ)
3.5156 0.1699 0.2849 0.4934
Índice de
comportamiento
al flujo (n)
0.9325 1.8478 1.3533 1.2596
r 0.99974 0.9733 0.9943 0.9965
Modelo matemático: τ=2.0085(Pa·s)ϒ1.0250
Tabla 10. Resultados de la segunda prueba hecha a la fase dispersa del malvavisco
tradicional con el viscosímetro de cilindros concéntricos (Descenso).
Gráfico 3. Curvas de ascenso y descenso de la segunda prueba de la fase continua del
malvavisco tradicional.

9.  Análisis de perfil del textura
 Análisis de perfil de textura; 2 ciclos de compresión
 Dimensiones de la muestra 2.5 x 2.5 x 2.5 cm
 Dispositivo empleado: placa circular de 7 cm de diámetro.
Dureza
(Kg)
Dist
comp
(Kgf
mm)
Elast
inst
AREA
COMP
C1
(Kgf
mm)
AREA
DESC
C1
RESILENCIA
ELAST.
TOTAL
AREA
COMP
C2
COHESIVIDAD GOMOSIDAD MASTICOSIDAD
MUESTRA
1
0.3754 8.697 0.8697 1.560 1.319 0.8454 0.8974 1.365 0.8754 0.3286 0.2949
MUESTRA
2
0.4397 9.210 0.9210 1.701 1.504 0.8844 0.9455 1.528 0.8984 0.3950 0.3735
MUESTRA
3
0.5185 9.146 0.9146 2.170 1.753 0.8078 0.9450 1.966 0.9058 0.4696 0.4438
MUESTRA
4
0.3837 8.049 0.8049 1.461 1.210 0.8285 0.8248 1.294 0.8857 0.3398 0.2803
MUESTRA
5
0.4708 8.675 0.8675 1.851 1.550 0.8378 0.9051 1.620 0.8755 0.4121 0.3730
Promedio 0.4376 8.755 0.8755 1.749 1.467 0.8408 0.9036 1.555 0.8882 0.3890 0.3531
Desviación
Estándar
0.0601 0.466 0.0466 0.278 0.211 0.0281 0.0493 0.264 0.0136 0.0573 0.0666
 Velocidad de penetración: 2.00 mm/s
 Distancia de penetración: 10 mm
Tabla 11. Resultados del análisis de perfil de textura: Formulación tradicional

10. Dureza  F: C2L/9.81, F = 0.4708 Kgf
Dist comp  D: (C2E-C3E), D = 8.675 Kgf mm
Elast inst  D/10 = 0.8675
AREA COMP C1  A1: (C2W-C1W)/9.81 = 1.851 Kgf mm
AREA DESC C1  A2: (C3W-C2W)/9.81 = 1.550
RESILENCIA  A2 / A1 = 0.8378
DIST COM. C2  D2: (C5E-C4E) = 9.051
ELAST TOTAL  ET: D2/10 = 0.9051
AREA COMP C2  A3: (C5W-C4W)/9.81 = 1.620
COHESIVIDAD  C: A3/A1 = 0.8755
GOMOSIDAD  F*C = 0.4121
MASTICOSIDAD  F*C*ET = 0.3730
Fig4. Curva de análisis de perfil de textura: formulación tradicional

11.  Prueba de punción
 1 ciclo
 Dimensiones de la muestra 2.5 x 2.5 x 2.5 cm
 Dispositivo empleado: cilindro plástico de 0.5 cm de diámetro
DUREZA
(Kgf.mm)
Fracturabilidad
(Kgf.mm)
Trabajo
Fract.
(Kgf.mm)
Distancia
Fract.
(Kg.mm)
Trabajo
Punción
(Kgf.mm)
Muestra 1 0.1016 0.1016 0.4717 10.01 0.4717
Muestra 2 0.0891 0.0891 0.4148 10.02 0.4148
Muestra 3 0.0871 0.0871 0.3831 9.917 0.3831
Muestra 4 0.0954 0.0954 0.4669 10.03 0.4669
Muestra 5 0.0933 0.0933 0.4193 9.999 0.4193
Promedio 0.0933 0.0933 0.4312 9.993 0.4312
Desviación
estándar
0.0057 0.0057 0.0376 0.044 0.0376
 Velocidad de penetración: 2.00 mm/s
 Distancia de penetración: 10 mm
Tabla 12. Resultados de la prueba de punción: Formulación tradicional
Gráfico 5. Curva de fuerza en función del tiempo: formulación tradicional

12. “Fracturabilidad es la fuerza con la cual un material se fractura, relacionada con
los parámetros primarios de dureza y cohesividad. Se mide como la altura de la
primera ruptura significativa en el primer pico”. Como se puede observar en la
gráfica 5., no se presentó fractura en el malvavisco de formulación tradicional.
FORMULACIÓN: AISLADO PROTEICO DE SOYA 6%
 Prueba de estabilidad
Formulación
Volumen
de la
mezcla
(mL)
Volumen
de
drenado
(mL)
Rendimiento
(%)
Promedio
Desviación
estándar
Tradicional
80 8 90.0000
89.7917 0.360880 8 90.0000
80 8.5 89.3750
Tabla 13. Estabilidad de la espuma: Formulación APS 6%
 Densidad
Muestra
Masa de
la caja
vacía (g)
Masa de
la caja
con
muestra
(g)
Volumen
de la caja
(cm3
)
Densidad
(g/cm3
)
Promedio
Desviación
estándar
1 6.94 22.6
50
0.3132
0.3056 0.00702 7.11 22.32 0.3042
3 6.85 21.82 0.2994
Tabla 14. Densidad de la espuma: Formulación APS 6%
 Tamaño de partícula
Muestra 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Tamaño 10 8 8 9 10 10 11 9 9 10 9 10 10 11 10 9 10 10 9 9
Promedio 9.55
Tamaño promedio (mm) 0.0239
Desviación estándar 0.8256
Tabla 15. Tamaño promedio de partícula: Formulación APS 6%

13. Figura 1. Espuma de la formulación APS 6%
FORMULACIÓN: AISLADO PROTEICO DE SOYA 6% + 0.2% CARRAGENINA
 Densidad
Muestra
Masa de
la caja
vacía (g)
Masa de
la caja
con
muestra
(g)
Volumen
de la caja
(cm3
)
Densidad
(g/cm3
)
Promedio
Desviación
estándar
1 6.94 29.7
50
0.4552
0.4361 0.01672 7.08 28.5 0.4284
3 6.87 28.1 0.4246
Tabla 16. Densidad de la espuma: Formulación APS 6% + carragenina 0.2 %
 Tamaño de partícula
Muestra 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Tamaño 9 9 11 9 11 9 9 12 10 9 11 11 9 9 12 10 9 11 11 9
Promedio 10.00
Tamaño promedio (mm) 0.0250
Desviación estándar 1.1239
Tabla 17. Tamaño promedio de partícula: Formulación APS 6%+carragenina 0.2 %

14. FORMULACIÓN: AISLADO PROTEICO DE SOYA 6% + 0.6% goma gelana
 Densidad
Muestra
Masa de
la caja
vacía (g)
Masa de
la caja
con
muestra
(g)
Volumen
de la caja
(cm3
)
Densidad
(g/cm3
)
Promedio
Desviación
estándar
1 7.7 40.64
50
0.6588
0.5949 0.07922 7.6 38.58 0.6196
3 7.6 32.91 0.5062
Tabla 18. Densidad de la espuma: Formulación APS 6% + goma gelana 0.6 %
FORMULACIÓN: AISLADO PROTEICO DE SOYA 6% + 0.6% carragenina
 Densidad
Muestra
Masa de
la caja
vacía (g)
Masa de
la caja
con
muestra
(g)
Volumen
de la caja
(cm3
)
Densidad
(g/cm3
)
Promedio
Desviación
estándar
1 7.11 30.05
50
0.4588
0.5065 0.04342 6.63 33.82 0.5438
3 6.66 32.5 0.5168
Tabla 19. Densidad de la espuma: Formulación APS 6% + carragenina 0.6 %