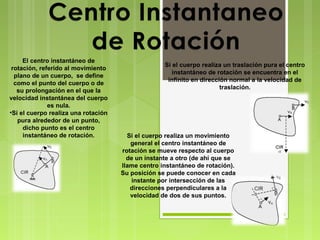
El documento define el centro instantáneo de rotación como el punto donde la velocidad de un cuerpo en movimiento plano es nula. Explica que durante una rotación pura, el centro es el punto de rotación, y durante una traslación pura, está en el infinito perpendicular a la velocidad. También describe cómo calcular los centros instantáneos de rotación para mecanismos como bielas y manivelas.

2. El centro instantáneo de
rotación, referido al movimiento
plano de un cuerpo, se define
como el punto del cuerpo o de
su prolongación en el que la
velocidad instantánea del cuerpo
es nula.
•Si el cuerpo realiza una rotación
pura alrededor de un punto,
dicho punto es el centro
instantáneo de rotación.
Si el cuerpo realiza un traslación pura el centro
instantáneo de rotación se encuentra en el
infinito en dirección normal a la velocidad de
traslación.
Si el cuerpo realiza un movimiento
general el centro instantáneo de
rotación se mueve respecto al cuerpo
de un instante a otro (de ahí que se
llame centro instantáneo de rotación).
Su posición se puede conocer en cada
instante por intersección de las
direcciones perpendiculares a la
velocidad de dos de sus puntos.

3. Tal como sugirió Reuleaux a
mediados del siglo XIX, los
eslabones se pueden considerar que
en cada instante realizan un giro
alrededor de un centro. Dicho centro
se llama centro instantáneo de
rotación o polo de velocidades.
Cuando un eslabón está efectuando
una traslación en un momento dado,
su centro instantáneo de rotación se
encuentra en el infinito y en una
dirección perpendicular al
movimiento del eslabón. Esto se
denota fácilmente porque las
velocidades de todos sus puntos
son iguales y sus vectores paralelos.

4. Para localizar los CIR seguimos el siguiente
método:
1) Hallar el número de centros (N = 4 (4 - 1)/2 = 6).
2) Determinar los inmediatos por simple
inspección.
3) Localizar el resto mediante la ley de los tres
centros.
En la figura muestra un mecanismo de
biela-manivela donde se han numerado
los eslabones desde el 1 hasta el 4. Al
disponer de 4 eslabones, el numero de
centros a localizar es de N = 4 (4 - 1)/2 =
6. Con objeto de no omitir ninguno de
los polos, se suele trazar un polígono
auxiliar de n = 4 vértices (a la derecha
de la figura) y se construyen con trazo
lleno los centros inicialmente
conocidos o inmediatos. Los polos
conocidos son P12, P23 y P14 que se
determinan de forma inmediata una vez
construida la figura.

5. Para calcular las velocidades por CIR seguiremos los pasos siguientes:
1. Identificar los eslabones a los que pertenecen:
a) El punto de velocidad conocida.
b) El punto de velocidad desconocida.
c) El eslabón de referencia o barra fija.
2. Se hallan los tres CIR relativos correspondientes a las barras, que estarán en línea recta según
nos indica el Teorema de Kennedy.
3. Se calcula la velocidad del CIR relativo de los dos eslabones no fijos, considerándolo como un
punto perteneciente a la barra de velocidad conocida.
4. Se considera la velocidad hallada como la de un punto del eslabón cuya velocidad queremos
hallar. Conociendo la velocidad de un punto del eslabón (CIR) y su centro de giro podemos
encontrar la de cualquier otro punto del mismo.
• Aplicación de los CIR a un mecanismo de cuatro barras.
• Aplicación de los CIR a un mecanismo de biela - manivela.

6. Para calcular las velocidades por CIR seguiremos los pasos siguientes:
1. Identificar los eslabones a los que pertenecen:
a) El punto de velocidad conocida.
b) El punto de velocidad desconocida.
c) El eslabón de referencia o barra fija.
2. Se hallan los tres CIR relativos correspondientes a las barras, que estarán en línea recta según
nos indica el Teorema de Kennedy.
3. Se calcula la velocidad del CIR relativo de los dos eslabones no fijos, considerándolo como un
punto perteneciente a la barra de velocidad conocida.
4. Se considera la velocidad hallada como la de un punto del eslabón cuya velocidad queremos
hallar. Conociendo la velocidad de un punto del eslabón (CIR) y su centro de giro podemos
encontrar la de cualquier otro punto del mismo.
• Aplicación de los CIR a un mecanismo de cuatro barras.
• Aplicación de los CIR a un mecanismo de biela - manivela.