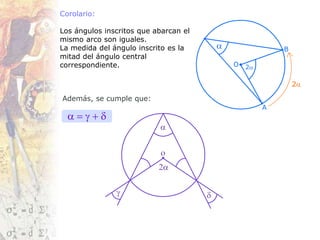
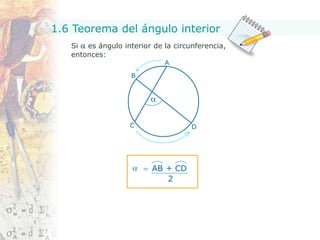
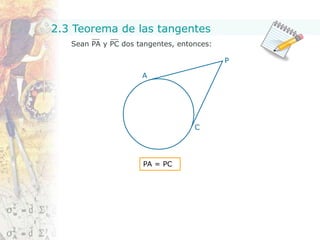
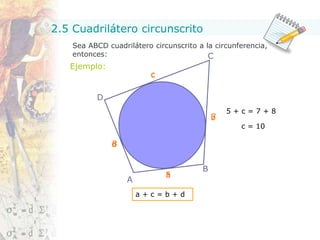
Este documento presenta conceptos fundamentales sobre figuras geométricas circulares. Explica teoremas clave relacionados con ángulos inscritos, triángulos y cuadriláteros inscritos en círculos, así como teoremas sobre secantes, tangentes y cuerdas. El objetivo es proporcionar una introducción básica a estas nociones geométricas.

1. Conceptos Fundamentales:
FIGURAS GEOMÉTRICAS
Conceptos Subsidiarios:
Circunferencia
Concepto operativo:
Teoremas de la Circunferencia
Colegio de Estudios Científicos y Tecnológicos del estado
de México Plantel Chimalhuacán
Profesores: Rocío Gamboa y
Oswaldo Camacho

2. Ángulo inscrito: Tiene el vértice en la circunferencia, y
mide la mitad del arco que subtiende.
Ejemplo:
Si el arco AB = 50º, entonces  = 25º
50°

3. Corolario:
Los ángulos inscritos que abarcan el
mismo arco son iguales.
La medida del ángulo inscrito es la
mitad del ángulo central
correspondiente.
2
Además, se cumple que:
 = g + d

4. Ejemplo:
En la figura, si arco AB mide 70°, entonces el ángulo del
centro AOB también mide 70° y el ángulo inscrito ACB
mide 35°.
O: centro de la circunferencia

5. 1.2 Igualdad de ángulos inscritos
Si dos o más ángulos inscritos subtienden el mismo
arco, éstos son iguales.
 = b = g

6. 1.3 Triángulo inscrito en una semicircunferencia
Todo triángulo inscrito en una semicircunferencia es
rectángulo con hipotenusa igual al diámetro.
180°
O: centro de la circunferencia

7. 1.4 Cuadrilátero inscrito en una circunferencia
En todo cuadrilátero inscrito en una circunferencia,
los ángulos opuestos son suplementarios.
 + b = 180°
g + d = 180°
Ejemplo:

8. 1.5 Teorema del ángulo exterior
Si  es ángulo exterior de la circunferencia,
entonces:

9. 1.6 Teorema del ángulo interior
Si  es ángulo interior de la circunferencia,
entonces:

10. 2. Teoremas fundamentales (trazos)
2.1 Teorema de las secantes
Sean PA y PB dos secantes, entonces:
PA ∙ PD = PB ∙ PC

11. Ejemplo:
12
20
6
x
12 ∙ PD = 20 ∙ 6
12 ∙ PD = 120
PD= 10
PA ∙ PD = PB ∙ PC
En la figura, determinar PD si PA = 12, PB = 20 y PC = 6.
PA y PB secantes.

12. 2.2 Teorema de la tangente y secante
Sean PA una tangente y PC una secante, entonces:
(PA)2 = PC ∙ PD

13. 2.3 Teorema de las tangentes
PA = PC
Sean PA y PC dos tangentes, entonces:

14. 2.4 Teorema de las cuerdas
Sean AB y CD dos cuerdas, entonces:
AP ∙ PB = CP ∙ PD

15. 2.5 Cuadrilátero circunscrito
a + c = b + d
5 + c = 7 + 8
c = 10
Ejemplo:
Sea ABCD cuadrilátero circunscrito a la circunferencia,
entonces: