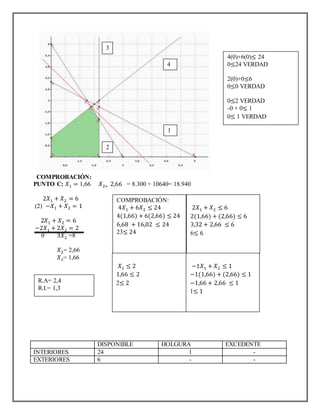
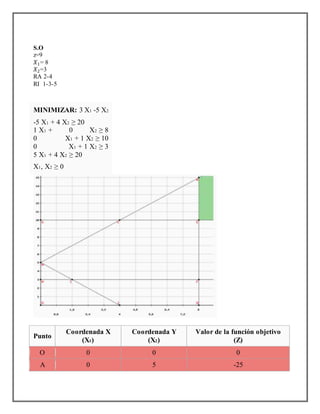
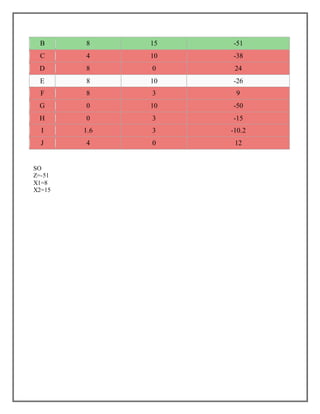
Este documento presenta tres problemas de programación lineal. El primer problema involucra maximizar las utilidades de una fábrica de pintura sujeto a restricciones en los recursos disponibles. El segundo problema busca minimizar la suma de dos variables sujeto a restricciones. El tercer problema busca maximizar una función objetivo lineal sujeto a restricciones en cinco desigualdades.

1. UNIVERSIDAD NACIONAL DE CHIMBORAZO
FACULTAD DE CIENCIAS POLITICAS Y ADMINISTRATIVAS
RIOBAMBA ECUADOR
ESCUELA: CONTABILIDAD Y AUDITORÍA DOCENTE: Doctor Marlon Villa Villa
Ms.C.
DISCENTE: RUBÍ PARRA FECHA: 2.014-10-20 SEMESTRE: 5º “A”
TEMA: MÉTODO GRÁFICO
1. INDICACIONES GENERALES
 La presente Prueba será calificada sobre 4 puntos
 Cada problema resuelto vale un punto excepto el tercero que vale 2 puntos
 El tiempo estimado para la prueba es de 50 minutos

2. C U E S T I O N A R I O.
Hallar el valor óptimo, la solución óptima, las restricciones activas, las restricciones inactivas, la
holgura o el excedente de los siguientes problemas
1. Una fábrica de pintura produce pinturas para interiores y exteriores, a partir de dos materias
primas M1 y M2. Por cada tonelada de pintura para interiores se requiere 4 toneladas de M1
y 2 toneladas de M2. Y para cada tonelada de pintura para exteriores se requiere 6 toneladas
de M1 y una de M2. Se dispone de 24 toneladas de M1 y 6 de M2 diariamente. La utilidad
que arroga una tonelada de pintura para exteriores es de $ 5 000 y de una tonelada para
interiores es de $4 000. La demanda máxima diaria de pintura para interiores es de 2
toneladas. Además la demanda diaria de pintura para interiores no puede exceder a la de
pintura para exteriores por más de una tonelada. La compañía quiere determinar la mezcla
de producción óptima de pinturas para interiores y exteriores que maximice las utilidades
diarias y satisfaga las limitaciones.
MAX: 5000X+4000푋2
S.A. 4푋1 + 6푋2 ≤ 24
2푋1 + 푋2 ≤ 6
−푋1 + 푋2 ≤ 1
푋1 ≤ 2
1 2 4
4푋1 + 6푋2 = 24 1 푋1 푋2
2푋1 + 푋2 = 6 2
푋= 2 3
0
4
1 −푋1 + 푋2 = 1 4
0
6
푋1 푋2
0 6
3 0
푋1 푋2
0 1
0
-1

2. 3
4
2
1
COMPROBACIÓN:
PUNTO C: 푋1 = 1,66 푋2= 2,66 = 8.300 + 10640= 18.940
2푋1 + 푋2 = 6
(2) −푋1 + 푋2 = 1
2푋1 + 푋2 = 6
−2푋1 + 2푋2 = 2
0 3푋2 =8
푋2= 2,66
푋1= 1,66
4(0)+6(0)≤ 24
0≤24 VERDAD
2(0)+0≤6
0≤0 VERDAD
0≤2 VERDAD
-0 + 0≤ 1
0≤ 1 VERDAD
COMPROBACIÓN:
4푋1 + 6푋2 ≤ 24
4(1,66) + 6(2,66) ≤ 24
6,68 + 16,02 ≤ 24
23≤ 24
2푋1 + 푋2 ≤ 6
2(1,66) + (2,66) ≤ 6
3,32 + 2,66 ≤ 6
6≤ 6
푋1 ≤ 2
1,66 ≤ 2
2≤ 2
−1푋1 + 푋2 ≤ 1
−1(1,66) + (2,66) ≤ 1
−1,66 + 2,66 ≤ 1
1≤ 1
DISPONIBLE HOLGURA EXCEDENTE
R.A= 2,4
R.I.= 1,3
INTERIORES 24 1 -
EXTERIORES 6 - -

3. PREGUNTA N°2
Minimizar: Z= 3F+ 4G
1. 퐹 + 퐺 ≥ 8
F G
0 8
8 0
2. 2퐹 + 퐺 ≥ 12
F G
0 12
6 0
3. 퐺 ≥ 2
4. 퐹 ≤ 10
퐹, 퐺 ≥ 0

4. 푭+푮=ퟖ
ퟐ푭+푮=ퟏퟐ (−ퟏ)
−푭= −ퟒ
푭=ퟒ
푭 + 푮 = ퟖ
ퟒ(ퟏ) + 푮 = ퟖ
ퟒ + 푮 = ퟖ
푮 = ퟖ − ퟒ
푮 = ퟒ
풁 = ퟑ푭 + ퟒ푮
풁 = ퟑ(ퟒ) + ퟒ(ퟒ)
풁 = ퟐퟖ
VALORES ÓPTIMOS
Z 28
F 4
G 4
r.a 1,2
r.i 3,4
HOLGURAS O EXCEDENTES
1.
푭 + 푮 + 푯ퟏ = ퟖ
ퟒ + ퟒ + 푯ퟏ = ퟖ
푯ퟏ = ퟖ − ퟖ
푯ퟏ = ퟎ
2.
ퟐ푭 + 푮 + 푯ퟐ = ퟏퟐ
ퟐ(ퟒ) + ퟒ + 푯ퟐ = ퟏퟐ
푯ퟐ = ퟏퟐ − ퟏퟐ
푯ퟐ = ퟎ
3.
푮 − 푯ퟑ = ퟐ
ퟒ − 푯ퟑ = ퟐ
−푯ퟑ = ퟐ − ퟒ
−푯ퟑ = −ퟐ
푯ퟑ = ퟐ
(excedente)
4.
푭 + 푯ퟒ = ퟏퟎ
ퟒ + 푯ퟒ = ퟏퟎ
푯ퟒ = ퟏퟎ − ퟒ
푯ퟒ = ퟔ
(holgura)

5. 3. Para el siguiente problema de programación lineal:
FUNCIÓN OBJETIVO: MAXIMIZAR
1) 5X1 – 4X2 = -20
x y
0
5
-4
0
2) X1 = 8
3) X2 = 10
4) X2 = 3
5) 5X1 + 4X2 =20
x y
0
5
4
0

6. S.O
z=9
푋1= 8
푋2=3
RA 2-4
RI 1-3-5
MINIMIZAR: 3 X1 -5 X2
-5 X1 + 4 X2 ≥ 20
1 X1 + 0 X2 ≥ 8
0 X1 + 1 X2 ≥ 10
0 X1 + 1 X2 ≥ 3
5 X1 + 4 X2 ≥ 20
X1, X2 ≥ 0
Punto
Coordenada X
(X1)
Coordenada Y
(X2)
Valor de la función objetivo
(Z)
O 0 0 0
A 0 5 -25

7. B 8 15 -51
C 4 10 -38
D 8 0 24
E 8 10 -26
F 8 3 9
G 0 10 -50
H 0 3 -15
I 1.6 3 -10.2
J 4 0 12
SO
Z=-51
X1=8
X2=15