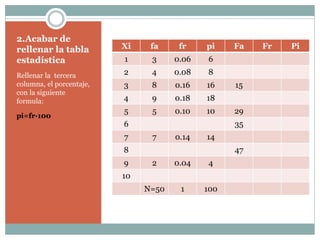
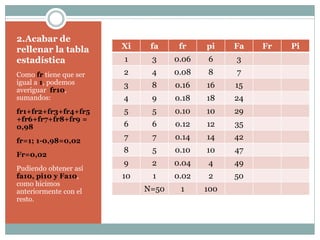
El resumen analiza los resultados de un examen realizado a 50 alumnos. Presenta los datos en una tabla estadística con las notas obtenidas (del 1 al 10), la frecuencia absoluta, la frecuencia relativa, el porcentaje y la frecuencia acumulada de cada nota. Calcula valores estadísticos como la media (4,98), la mediana (5) y la moda (4). También determina que el 35% de los alumnos obtuvieron una nota superior a 3, el 12% una nota de 6, y el 52% superaron el 4. La desviación

1. A N Á L I S I S E S T A D Í S T I C O D E U N E X A M E N
R E A L I Z A D O A U N G R U P O D E A L U M N O S
Tabla estadística

2. Las notas
obtenidas por los
alumnos fueron
catalogadas de 1
a 10.
Completar el
cuadro con los
resultados
obtenidos tras
realizar las
correspondientes
formulas.
Xi fa fr pi Fa Fr Pi
1 3 0.06
2 4
3 0.16 15
4 9 0.18
5 5 29
6 35
7 7 0.14
8 47
9 2
10
N=

3. 1. Número de
alumnos que se
han examinado
Para averiguar el nº de
alumnos que se han
examinado utilizaremos
los datos que nos
proporciona la tabla de
los alumnos que han
sacado un 1 en el
examen, a partir de la
fa y la fr, despejando
N.
fa/N=fr
3/N=0,06
N=3/0,06
N=50
Se han examinado 50 alumnos
N=50
Xi fa fr pi Fa Fr Pi
1 3 0.06
2 4
3 0.16 15
4 9 0.18
5 5 29
6 35
7 7 0.14
8 47
9 2
10
N=50

4. 2.Acabar de
rellenar la tabla
estadística
Para terminar de
completar la columna
de fa y fr, utilizamos la
formula :
fr=fa/N en el caso de
que dispongamos del
resultado de fa y de N.
Y utilizaremos la
fórmula despejada
fa=fr·N en el caso de
que dispongamos de la
fr y N.
Xi fa fr pi Fa Fr Pi
1 3 0.06
2 4 0.08
3 8 0.16 15
4 9 0.18
5 5 0.10 29
6 35
7 7 0.14
8 47
9 2 0.04
10
N=50 1

5. 2.Acabar de
rellenar la tabla
estadística
Rellenar la tercera
columna, el porcentaje,
con la siguiente
formula:
pi=fr·100
Xi fa fr pi Fa Fr Pi
1 3 0.06 6
2 4 0.08 8
3 8 0.16 16 15
4 9 0.18 18
5 5 0.10 10 29
6 35
7 7 0.14 14
8 47
9 2 0.04 4
10
N=50 1 100

6. 2.Acabar de
rellenar la tabla
estadística
Completar la cuarta
columna, FA, con la
siguiente formula:
Fa1=fa1
Fa2=fa1+fa2
Fa4=fa3+fa4
Xi fa fr pi Fa Fr Pi
1 3 0.06 6 3
2 4 0.08 8 7
3 8 0.16 16 15
4 9 0.18 18 24
5 5 0.10 10 29
6 35
7 7 0.14 14
8 47
9 2 0.04 4
10
N=50 1 100

7. 2.Acabar de
rellenar la tabla
estadística
Para poder obtener el
nº de alumnos que ha
sacado un 6 y un 8 en
el examen, realizamos
los siguientes cálculos:
1. Fa5=29; Fa6=35
fa6=Fa6-Fa5; fa6=6
2.Fa7=42; Fa8=47
fa8=Fa8-Fa7; fa8=5
Pudiendo completar el
resto de fr , pi y Fa de
los huecos existentes.
Xi fa fr pi Fa Fr Pi
1 3 0.06 6 3
2 4 0.08 8 7
3 8 0.16 16 15
4 9 0.18 18 24
5 5 0.10 10 29
6 6 0.12 12 35
7 7 0.14 14 42
8 5 0.10 10 47
9 2 0.04 4 49
10
N=50 1 100

8. 2.Acabar de
rellenar la tabla
estadística
Como fr tiene que ser
igual a 1, podemos
averiguar fr10,
sumandos:
fr1+fr2+fr3+fr4+fr5
+fr6+fr7+fr8+fr9 =
0,98
fr=1; 1-0,98=0,02
Fr=0,02
Pudiendo obtener así
fa10, pi10 y Fa10,
como hicimos
anteriormente con el
resto.
Xi fa fr pi Fa Fr Pi
1 3 0.06 6 3
2 4 0.08 8 7
3 8 0.16 16 15
4 9 0.18 18 24
5 5 0.10 10 29
6 6 0.12 12 35
7 7 0.14 14 42
8 5 0.10 10 47
9 2 0.04 4 49
10 1 0.02 2 50
N=50 1 100

9. 2.Acabar de
rellenar la tabla
estadística
Podemos completar la
columna Fr de la
siguiente forma:
Fr1=fr1
Fr2=fr1+fr2
Fr3=fr2+fr3
Fr4=fr3+fr4
Y así sucesivamente,
además de rellenar la
última columna, Pi:
Pi=Fr·100
Xi fa fr pi Fa Fr Pi
1 3 0.06 6 3 0.06 6
2 4 0.08 8 7 0.14 14
3 8 0.16 16 15 0.3 30
4 9 0.18 18 24 0.48 48
5 5 0.10 10 29 0.58 58
6 6 0.12 12 35 0.7 70
7 7 0.14 14 42 0.84 84
8 5 0.10 10 47 0.94 94
9 2 0.04 4 49 0.98 98
10 1 0.02 2 50 1 100
N=50 1 100

10. 3.Nº de alumnos que han
obtenido una nota superior
a 3
4. % de alumnos que han
obtenido una nota igual a 6
Xi fa
4 9
5 5
6 6
7 7
8 5
9 2
10 1
Total 35 alumnos
Xi fa fr pi
6 6 0.12 12
Cuestiones
Porcentaje 12%

11. 5. % de alumnos que han
sacado una nota superior a 4
6. Nº de alumnos que han
obtenido una nota superior a
2 e inferior a 5
Xi pi
5 10
6 12
7 14
8 10
9 4
10 2
Total 52%
Xi fa
3 8
4 9
Total 17 alumnos
Cuestiones

12. Cuestiones
7.Calcula la media aritmética, la mediana y la moda
 Media aritmética:
(1·3)+(2·4)+(3·8)+(4·9)+(5·5)+(6·6)+(7·7)+(8·5)+(9·2)+(10·1)/50=x;
249/50=x; X=4,98
 Mediana: 5 (Deja el 50% de los casos a un lado y a otro)
 Moda: 4 (valor que más se repite)

13. Cuestiones
8. Hallar el rango, la varianza y la desviación típica
 Rango: valor mayor=10; valor menor=1 (diferencia entre el valor mayor
y el menor de la variable); X=10-1; X=97
 Varianza: S2=[(1501/40)]-(4,98)2]; S2=37,525-24,8004; S2=12,7246
 Desviación típica: Es la raíz cuadrada positiva de S2
S=+ √ 12,7246 = 3,567