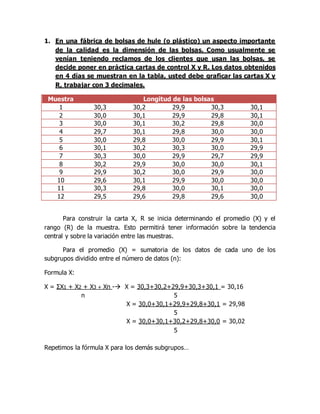
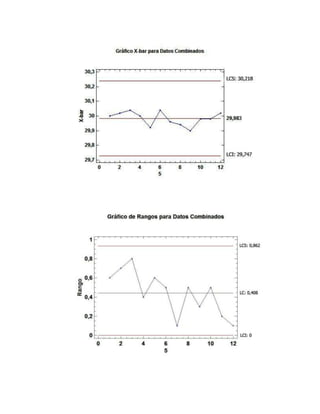
El documento describe un procedimiento para crear gráficos de control de X-barra y R para monitorear la calidad de bolsas plásticas producidas en una fábrica. Se recopilaron datos de longitud de 12 muestras tomadas a lo largo de 4 días. Se calculan los promedios, rangos, límites de control superior e inferior para cada gráfico. El análisis muestra que ningún punto está fuera de los límites de control, lo que indica que el proceso se encuentra bajo control estadístico.

1. República Bolivariana de Venezuela
Ministerio Popular para la Educación Superior
I.U.P “Santiago Mariño”
Escuela de Ingeniería Industrial (45)
Extensión Maturín
Profesora: Bachiller:
Xiomara Gutiérrez Ciro Buitrago CI: 19603391
Sección V
Maturín, Julio de 2014

2. 1. En una fábrica de bolsas de hule (o plástico) un aspecto importante
de la calidad es la dimensión de las bolsas. Como usualmente se
venían teniendo reclamos de los clientes que usan las bolsas, se
decide poner en práctica cartas de control X y R. Los datos obtenidos
en 4 días se muestran en la tabla, usted debe graficar las cartas X y
R, trabajar con 3 decimales.
Muestra Longitud de las bolsas
1 30,3 30,2 29,9 30,3 30,1
2 30,0 30,1 29,9 29,8 30,1
3 30,0 30,1 30,2 29,8 30,0
4 29,7 30,1 29,8 30,0 30,0
5 30,0 29,8 30,0 29,9 30,1
6 30,1 30,2 30,3 30,0 29,9
7 30,3 30,0 29,9 29,7 29,9
8 30,2 29,9 30,0 30,0 30,1
9 29,9 30,2 30,0 29,9 30,0
10 29,6 30,1 29,9 30,0 30,0
11 30,3 29,8 30,0 30,1 30,0
12 29,5 29,6 29,8 29,6 30,0
Para construir la carta X, R se inicia determinando el promedio (X) y el
rango (R) de la muestra. Esto permitirá tener información sobre la tendencia
central y sobre la variación entre las muestras.
Para el promedio (X) = sumatoria de los datos de cada uno de los
subgrupos dividido entre el número de datos (n):
Formula X:
X = ΣX1 + X2 + X3 + Xn - X = 30,3+30,2+29,9+30,3+30,1 = 30,16
n 5
X = 30,0+30,1+29,9+29,8+30,1 = 29,98
5
X = 30,0+30,1+30,2+29,8+30,0 = 30,02
5
Repetimos la fórmula X para los demás subgrupos…

3. Rango (R) = Valor mayor del subgrupo menos el valor menor:
Formula R:
R = X valor mayor – X valor menor  R = 30,3 – 29,9 = 0,4
R = 30,1 – 29,8 = 0,3
R = 30,2 – 29,8 = 0,4
Repetimos la formula R para los demás subgrupos…
Muestra Longitud de las bolsas Promedio Rango
1 30,3 30,2 29,9 30,3 30,1 30,16 0,4
2 30,0 30,1 29,9 29,8 30,1 29,98 0,3
3 30,0 30,1 30,2 29,8 30,0 30,02 0,4
4 29,7 30,1 29,8 30,0 30,0 29,92 0,4
5 30,0 29,8 30,0 29,9 30,1 29,96 0,3
6 30,1 30,2 30,3 30,0 29,9 30,1 0,4
7 30,3 30,0 29,9 29,7 29,9 29,96 0,6
8 30,2 29,9 30,0 30,0 30,1 30,04 0,3
9 29,9 30,2 30,0 29,9 30,0 30 0,3
10 29,6 30,1 29,9 30,0 30,0 29,92 0,5
11 30,3 29,8 30,0 30,1 30,0 30,04 0,5
12 29,5 29,6 29,8 29,6 30,0 29,7 0,5
X’= 29,983 R’= 0,408
Promedio Global (X’) = sumatoria de todos los valores medios y se divide
entre el número de subgrupos (k).
X’ = ΣX1 + X2 + X3 + Xn
k
X’=30,16+29,98+30,02+29,92+29,96+30,01+29,96+30,04+30+29,92+30,04+29,7
12
X’ = 29,983
Valor medio del Rango (R’) = sumatoria del rango (R) de cada uno de los
subgrupos dividido entre el número de subgrupos (k).
R’ = ΣR1 + R2 + R3 + Rn
k
R’ = 0,4+0,3+,0,4+,0,4+,0,3+,0,4+,0,6+,0,3+,0,3+,0,5+,0,5+,0,5 = 0,408
12

4. Límites de Control:
Para calcular los límites de control se utilizan los datos de la siguiente tabla:
n A2 D4 D3
2 1,880 3,267
3 1,023 3,575
4 0,729 2,282 0,076
5 0,577 2,115
6 0,483 2,004
7 0,419 1,924
Grafica X’:
Línea Central (LC) = X’ = 29,983
Límite de Control Superior (LCS) = X’ + A2R’
LCS = 29,983 + (0,577)(0,408)
LCS = 30,218
Límite de Control Inferior (LCI) = X’ – A2R’
LCI = 29,983 – (0,577)(0,408)
LCI = 29,747
Grafica R’:
Línea Central (LC) = R’ = 0,408
Límite de Control Superior (LCS) = D4R’
LCS = (2,115)(0,408)
LCS = 0,862
Límite de Control Inferior (LCI) = D3R’
LCI = (0,000)(0,408)
LCI = 0

6. Análisis:
Este procedimiento crea un gráfico de X-bar y R para Datos Combinados.
Está diseñada para permitirle determinar si los datos provienen de un proceso en
un estado de control estadístico. Las gráficas de control se construyen bajo el
supuesto de que los datos provienen de una distribución normal con una media
igual a 29,9833 y una desviación estándar igual a 0,189882. Estos parámetros
fueron estimados a partir de los datos. De los 12 puntos no excluidos mostrados
en la gráfica, 0 se encuentran fuera de los límites de control en la primera gráfica,
mientras que 0 están fuera de límites en la segunda. Puesto que la probabilidad
de que aparezcan 0 o más puntos fuera de límites, sólo por azar, es 1,0 si los
datos provienen de la distribución supuesta, no se puede rechazar la hipótesis de
que el proceso se encuentra en estado de control estadístico con un nivel de
confianza del 95%.