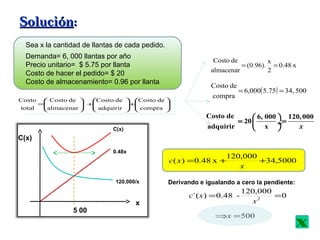
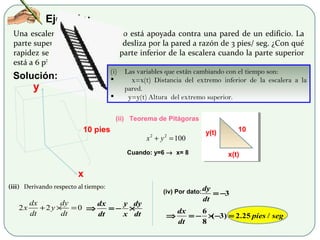
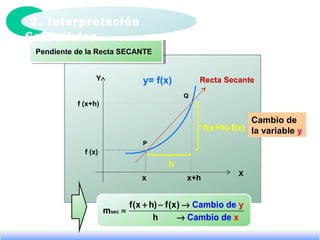
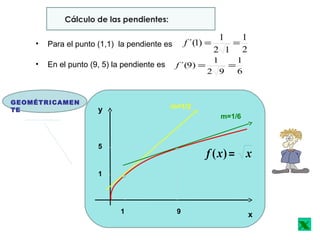
El documento trata sobre el concepto de derivada de una función. Explica que la derivada estudia el cambio que ocurre en una cantidad cuando ocurren variaciones en otras cantidades de las cuales depende. Incluye ejemplos como el cambio en el PNB del Perú con cada año o el cambio en el costo total de operación de una planta con cada unidad adicional producida. También presenta conceptos como la interpretación geométrica de la derivada, teoremas fundamentales y derivadas de funciones especiales.

1. DERIVADA DE UNADERIVADA DE UNA
FUNCIÓNFUNCIÓN

2. CÁLCULO DIFERENCIAL
El cambio en el producto nacional bruto del Perú con
cada año que pasa.
Estudia el cambio que ocurre
en una cantidad cuando
ocurren variaciones en otras
cantidades de las cuales
depende.
El cambio en el costo total de operación de
una planta que resultan de cada unidad
adicional producida.
El cambio en la demanda de cierto producto que resulta de
un incremento de una unidad (por ejm., S/.1) en el precio.

3. CONTENIDO
Motivación
1. Definición de la derivada de una función
2. Interpretación geométrica
3. Ejemplos de derivadas
4. Teoremas Fundamentales
5. Derivadas de funciones especiales
6. Ejemplo de Aplicación

4. MOTIVACIÓN

5. “Trazar una recta tangente a la gráfica de una
función en un punto dado de ella” Siglos: XVI-XVII
“Trazar una recta tangente a la gráfica de una
función en un punto dado de ella” Siglos: XVI-XVII
SURGIMIENTO DE LA DERIVASURGIMIENTO DE LA DERIVA
Como determinar la velocidad de un
cuerpo en movimiento rectilíneo en un
instante dado (velocidad instantánea)
Problema Físico
Problema Geométrico
Intuitivamente: “Recta que toca
a la curva en un solo punto”
Leibniz
Newton
Distancia recorrida
por la pelota: e=f(t)
¿Cuánto habrá recorrido al cabo de 2s?
¿Qué velocidad llevará en ese instante?

6. ¿Cambia la posición del felino?
• ¿Varía la posición
de su cuerpo?
• ¿Respecto de que
variable física
percibes esa
variación?
El tiempo es fundamental en muchos de los
procesos de variación.
Observa con atención:

7. ¿La paloma se desplaza?
¿Te podrás
imaginar cuánto
se mueve en:
• Un minuto ...
• Un segundo ...
• Una décima de
segundo ...
• Una milésima de
segundo ...
¿Qué tan pequeño puede
ser el tiempo para que
percibas el movimiento?

8. ¡A veces la variación es lenta!
• ¿Qué magnitudes
físicas crees que
varían en este caso?
• La relación de
variación se puede
considerar respecto
de dos variables
mutuamente
dependientes.Aquí se observa una relación
desplazamiento/tiempo
Aquí se observa una relación
desplazamiento/tiempo
x
y
∆
∆

9. x
xfxxf
x
y
∆
−∆+
=
∆
∆ )()(
x
xfxxf
x ∆
−∆+
→∆
)()(
lim
0

10. ¡Ahora imagina cuantas derivadas
habrá en este equipo!
¿Puedes proponer alguna?

11. CONTROL DE INVENTARIOCONTROL DE INVENTARIO
Un fabricante de bicicletas compra 6, 000 llantas al año a
un distribuidor. El gasto de manejo y transporte es $ 20
por pedido, el costo de almacenamiento es 96 centavos
por llanta al año y cada llanta cuesta $ 5.75. Suponga que
las llantas se utilizan a una tasa constante durante todo
el año y que cada pedido llega justo cuando se está
acabando el pedido anterior. ¿Cuál es la cantidad que se
debe ordenar en cada pedido para minimizar el costo?
x

12. 1. Definición
Sea f una función dada. La derivada de f
respecto a x, denotada por , es otra
función definida por:
dx
df
h
xfhxf
xf
dx
df
h
)()(
lim)('
0
−+
==
→
Si este límite existe.
Ejemplo:
1) Dada la función definida por: f(x)= x. Determinar la derivada de f.1) Dada la función definida por: f(x)= x. Determinar la derivada de f.
1lim
)()(
lim
)()(
lim)('
000
==/−+/=
−+
=
→→→ h
h
h
xhx
h
xfhxf
xf
hhh
Por lo tanto: 1)´()(' == xxf
Resolución
x

13. x x+h
X
Y y= f(x)
f (x)
f (x+h)
Recta Secante
f(x+h)-f(x)
h
P
Q
2. Interpretación
Geométrica
sec
Cambio df(x h) f(x) e
Camb
m
io
y
de xh
+ − →
=
→
Pendiente de la Recta SECANTE
Cambio de
la variable y

14. x x+h
X
Y y=f(x)
f(x)
f (x+h)
Recta Tangente
P
Q Recta Secante
)('
)()(
limlim
0
sec
0
xf
h
xfhxf
mm
hh
tg =
−+
→
=
→
=
Pendiente de la Recta TANGENTEPendiente de la Recta TANGENTE
PQ →
R. Sec. → R. Tangente
tgmm →sec
x

15. Cálculo de las pendientes:
• Para el punto (1,1) la pendiente es
2
1
12
1
)1´( ==f
• En el punto (9, 5) la pendiente es
6
1
92
1
)9´( ==f
1
1
xxf =)(
m=1/2
m=1/6
9 x
5
y
GEOMÉTRICAMEN
TE
x

16. 4. TEOREMA FUNDAMENTALES4. TEOREMA FUNDAMENTALES
Si f y g son funciones derivables y k, a, b y c son
constantes entonces:
1. [k f(x)]´=k f´(x)
2. [a f(x) ± b g(x)]´= a f´(x) ± b g´(x)
3. [f(x).g(x)]´=f´(x).g(x)+f(x).g´(x) Regla del producto
4. Regla del cociente
5. (fg)´(x)=[f(g(x))]´=f´(g(x)).g´(x) Regla de la Cadena
Si f y g son funciones derivables y k, a, b y c son
constantes entonces:
1. [k f(x)]´=k f´(x)
2. [a f(x) ± b g(x)]´= a f´(x) ± b g´(x)
3. [f(x).g(x)]´=f´(x).g(x)+f(x).g´(x) Regla del producto
4. Regla del cociente
5. (fg)´(x)=[f(g(x))]´=f´(g(x)).g´(x) Regla de la Cadena
´
2
( ) '( ) ( ) ( )´. ( )
( ) ( )
f x f x g x g x f x
g x g x
  −
= 
 
x

17. 5. DERIVADAS DE FUNCIONES ESPECIALES5. DERIVADAS DE FUNCIONES ESPECIALES
Función
f(x)
Derivada
f´(x)
K 0
, x≠0
n
x 1−n
nx
x x2
1
xln x
1
u
a ln 'u
a a u
xsen xcos
xcos xsen−
[ ] 025 ´
=−
=)´3( 4
x 3
12x
=+ )´1( x 12
1
+x
xxx
eeee == ln.)´(
http://www.terra.es/personal2/jpb00000/tabladerivadas.htm x

18. Determinar las derivadas de la funciones siguientes:Determinar las derivadas de la funciones siguientes:
1.
)´12()´5()´2()´( 34
xxxxf −+=
xxxxf 1252)( 34
−+=
Solución
12158 23
−+= xx
2. xsenxxf 5
3)( =
Solución:
Se aplicará la derivada de un
producto
)´)(3())´(3()´( 55
xsenxxsenxxf +=
xxxsenx cos315 54
+=
3.
x
x
xf
ln
)(
6
=
Solución: Se aplicará la derivada de un
cociente
´6 6 6
2
( )´(ln ) ( )(ln )´
´( )
ln (ln )
x x x x x
f x
x x
  −
= = ÷
 
5 6
2
5 5
2
1
(6 )(ln ) ( )( )
ln
6 ln
ln
x x x
x
x
x x x
x
− /
/=
−
=
4. )19(cos)( 2
−= xxf
Solución: Aplicando la Regla de la
cadena
( ) )´19´()19(cos)´( 22
−−= xxxf
)19(18 2
−−= xsenx
x

19. 6. Aplicación:6. Aplicación: CONTROL DE INVENTARIOCONTROL DE INVENTARIO
Un fabricante de bicicletas compra 6, 000 llantas al
año a un distribuidor. El gasto de manejo y transporte
es $ 20 por pedido, el costo de almacenamiento es 96
centavos por llanta al año y cada llanta cuesta $ 5.75.
Suponga que las llantas se utilizan a una tasa
constante durante todo el año y que cada pedido llega
justo cuando se está acabando el pedido anterior.
¿Cuál es la cantidad que se debe ordenar en cada
pedido para minimizar el costo?

20. compra
deCosto
adquirir
deCosto
almacenar
deCosto
total
Costo






+





+





=
x0.48
2
x
(0.96).
almacenar
deCosto
==
Costo de 6, 000 120,000
20
adquirir x x
 
= = ÷
 
( ) 50034,75.5000,6
compra
deCosto
==
5000,34
000,120
x48.0)( ++=
x
xc
Sea x la cantidad de llantas de cada pedido.
Demanda= 6, 000 llantas por año
Precio unitario= $ 5.75 por llanta
Costo de hacer el pedido= $ 20
Costo de almacenamiento= 0.96 por llanta
x
C(x)
5 00
0.48x
120,000/x
C(x)
Derivando e igualando a cero la pendiente:
0
000,120
-48.0)´( 2
==
x
xc
500=⇒x
x
SoluciónSolución::

21. Docente: Ernaldo Caruajulca Muñoz ..
APLICACIONES DELA DERIVADAAPLICACIONES DELA DERIVADA

22. CONTENIDO
1. Diferenciación Implícita
2. Razón de Cambio
3. Tasas de Cambio Relacionadas

23. DIFERENCIACIÓN
IMPLÍCITA

24. FUNCIÓN IMPLÍCITAFUNCIÓN IMPLÍCITAFUNCIÓN IMPLÍCITAFUNCIÓN IMPLÍCITA Examinar la función: 5
y y x 0+ + =
X
Y
-2
2
Hallar la pendiente de la recta
tangente a esta curva en (2, -1)
( )5
0y y x
dy dy
dx d
( )
x
+ + =
( )5
0
dy dy dy dy
dx dx dx
y (y) (x) ( )
dx
+ + =
4 dy dy
dx d
5y 1
x
0+ + =
4 4
dy 11
5( 1) 1
1
1x 65yd
− −
− +
= = −
+
=
(2,-1)

25. Ejemplo:
Calcular la derivada d ela función:Calcular la derivada d ela función: 53 22
=+ yx
Por lo tanto:
xx 6)2(3 =
Solución:
)´5()´3( 22
=+ yx
´2 yy ⋅ 0
DERIVACIÓN IMPLÍCITA
 Una función y=f (x) se llama implícita cuando está definida en la forma
F(x,y) = 0.
 En muchas ocasiones se desea derivar funciones que tienen esta forma
donde es difícil o no se puede despejar la variable y.
 En tales casos se derivará directamente la expresión, teniendo en cuenta
que y es una función de x. Por ello cuando se derive y, se escribirá y´.
6 2 ´ 0x y y⇒ + × =
3
´y
x
y
= −

26. MÉTODO PRÁCTICO
Si E(x,y)=0 define implícitamente a y=f(x). Para obtener , es
suficiente:
´y
x
dy
d
=
´
´
x
y
Eyd
dx E
= −
Donde: E´x es la derivada de E(x,y) respecto a x considerando a y
constante. E´y es la derivada de E(x,y) respecto a y considerando a y
constante.
En el ejemplo anterior se tiene:
2 2
3 5x y+ =
2 2
( , ) 3 5E x y x y⇒ = + −
Aplicando la fórmula anterior, se obtiene:
6
2
x
y
E x
E y
=
=
6
2
3y x x
y
d
x yd
= − = −

27. La producción semanal de una
compañía es $ 384 000 y su producción
se relaciona con las horas de trabajo
“x”, y los dólares de inversión de
capital “y”,
Hallar e interpretar la razón de cambio
de la inversión de capital respecto de
las horas de trabajo cuando las horas de
trabajo son 512 y la inversión de capital
es de $64000.
1 2/3/3
30384000 = yx
APLICACIÓN

28. Solución:
Calcular por derivación implícita
2
dy
dx
y
x
= −
64000
2(512)
dy
62.5
dx
= = −−
Y=$ Inversión del
capital = 64000
Horas de trabajo
= 512 horas
dy
dx
Derivando implícitamente:
Interpretación: La inversión de capital para mantener producción
semanal= $ 384, 000 disminuye $62.5 por hora de
trabajo adicional a un nivel de horas de 512.
Inversión
Hora de
Trabajo
Al aumentar en 1 hora de
trabajo , se obtendrá un
ahorro de $62.5

29. ´
dy
dx
y=Se sabe:
´dy dy x= ×
NOTANOTA

30. RAZÓN DE CAMBIO

31. En general, una razón de cambio con respect o al t iempo es
la respuest a a est a pregunt a.
¿Cuán rápido varía una
cantidad?
Mientras que:
La derivada dy/dx de una función y=f(x) es una
razón de cambio instantánea con respecto a la
variable x.
Si Y=Posición o distancia (t) =f (t)
Razón de Cambio con
respecto al tiempo = velocidad

32. Velocidad Promedio
t
Si la velocidad
fuese constante:
El movimiento de un automóvil en una carretera
está esencialmente determinado si conocemos su
posición s como función del tiempo: s=s(t).
s
v
s
t
=
Velocidad Instantánea
s t S t
t t
v 2 1
2 1
( ) ( )−
−
=
2 1
2 1
2 1
( ) )
lim
(
→
−
−
= =
t t
v
S t S t dS
t t dt

33. Este concepto de velocidad en el movimiento
rectilíneo corresponde al concepto más general de
tasa o razón instantánea de cambio.
La razón de cambio corresponde para dos
variables x e y que están relacionadas por una
relación funcional:
y=f(x)
La razón de cambio en x1 es:
f´(x1)
0
lim
∆ →
∆
∆x
y
x

34. RAZÓN DE CAMBIO
Si x varía de xl a (xl +∆x), entonces y varía de f(xl) a f(xl +∆x).
Entonces:
1 1
1
0 0
( ) ( )
'( ) lim lim
x x
f x x f x y
f x
x x∆ → ∆ →
+ ∆ − ∆
= =
∆ ∆
1 1( ) ( )y f x x f x∆ = + ∆ − x∆ Incremento de y:  Incremento de x:
Muestra el cambio de la variable y
Muestra el cambio de la variable x
1
0
´( ) lim
x
y
f x
x∆ →
∆
=
∆
Razón de cambio instantáneaRazón de cambio instantánea
1 1( ) ( )f x x f x y
x x
+∆ − ∆
=
∆ ∆
Tasa Promedio de variación de y
por una unidad de variación de x :
Tasa o razón de cambio
Si: y=f(x), entonces la razón de cambio instantánea de y por unidad
de variación de x en xl es f´(xl), si éste existe.

35. EJEMPLOEJEMPLO
Suponga que C(x) dólares es el costo total por la fabricación de x
sillas, y que: 2
( ) 110 4 0.02C x x x= + +
Determine: (a) La función costo marginal C´
(b) La razón de cambio cuando x=50
(a) Derivando se obtiene:
Solución:
´( ) 4 0.04C x x= +
(b) Razón de cambio: ´(50) 4 0.04(50)
6
C = +
=
La razón de cambio cuando se fabrican
50 sillas es de $6 por silla.

36. Si dos cantidades están relacionadas entre sí, entonces cuando
una de ellas cambia con el tiempo, la otra cambiará también. Por
lo tanto sus razones de cambio (con respecto al tiempo) están
relacionadas entre sí. Por ello a este tipo de situaciones se les
llama razones de cambio relacionadas.
Si dos cantidades están relacionadas entre sí, entonces cuando
una de ellas cambia con el tiempo, la otra cambiará también. Por
lo tanto sus razones de cambio (con respecto al tiempo) están
relacionadas entre sí. Por ello a este tipo de situaciones se les
llama razones de cambio relacionadas.
RAZONES DE CAMBIO RELACIONADAS
http://docentes.uacj.mx/sterraza/matematicas_en_movimiento/razrel/raz_ejem.html

37. Ejemplo:
Una escalera de 10 pies de largo está apoyada contra una pared de un edificio. La
parte superior de la escalera se desliza por la pared a razón de 3 pies/ seg. ¿Con qué
rapidez se aleja del edificio la parte inferior de la escalera cuando la parte superior
está a 6 pies del suelo?
x
y
10 pies
Solución:
(i) Las variables que están cambiando con el tiempo son:
 x=x(t) Distancia del extremo inferior de la escalera a la
pared.
 y=y(t) Altura del extremo superior.
(ii) Teorema de Pitágoras
2 2
100x y+ =
10y(t)
x(t)
(iii) Derivando respecto al tiempo:
2 2 0
dx dy
x y
dt dt
+ × =
dx y dy
dt x dt
⇒ = − ×
Cuando: y=6 → x= 8
(iv) Por dato: 3
dy
dt
= −
6
( 3) 2.25 /
8
dx
pies seg
dt
⇒ = − ×− =