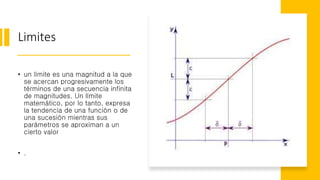
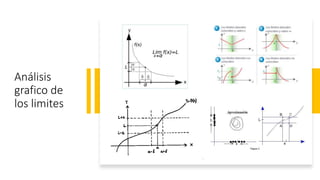
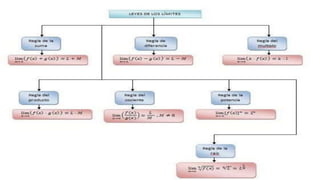
Este documento define conceptos clave como incremento, tasa de cambio y límite. Un incremento representa el cambio en el valor de una variable entre dos puntos. La tasa de cambio promedio mide el cambio en la variable dependiente dividido por el cambio en la variable independiente entre dos puntos. Un límite describe el valor al que se aproxima una función cuando su variable se acerca a un valor particular.

1. INCREMENTOS Y TASAS
LIMITES
UNIVERSIDAD DEL TOLIMA

2. INCREMENTO
• cuando una cantidad variable pasa de un valor inicial a otro valor, se dice que ha
tenido un incremento. Para calcular este incremento basta con hallar la diferencia
entre el valor final y el inicial.
• Para denotar esta diferencia se utiliza el símbolo Dx, que se leee "delta x". El
incremento puede ser positivo o negativo, dependiendo de si la variable aumenta
o disminuye al pasar de un valor a otro. Por ejemplo, si el valor inicial de una
variable x, x1, es igual a 3, y el valor final x2 es igual a 7, el incremento Dx = x2 -
x1 = 7 - 3 = 4: la variable se ha incrementado positivamente en 4 unidades. En
cambio, si el valor inicial es 7 y el valor final 3, Dx = x2 - x1 = 3 - 7 = -4: la variable
ha tenido un incremento negativo (decremento) de 4 unidades.

3. Formula de los
incrementos
• Ay= f(x +△ 𝑥) − 𝑓(𝑥)

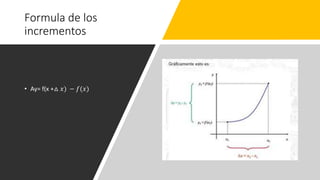
4. • Determine los incrementos de cada función
• 1. . f(x)=2x + 7 ; Si x=3 y Δx= .2
• Remplazando en
• Δy=f(x1 + Δx) – f(x1)
• Δy=f(3 + 0.2) – f(3)=f(3.2)-f(3)=[2(3.2)+7)]-[2(3)+7]
• Δy=(6.4+7)-(6+7)=13.4-13
• Δy=0.4
• Es decir que un incremento de x en 0.2 genera un
0.4

5. Es decir que cuando el incremento de x es de 0.5 se
incrementa en 1.4

6. Ejemplos aplicativos
• Un fabricante descubre que el costo de producir x artículos está dado por
C=0,001𝑥3
− 0,3𝑥2
+ 40𝑥 + 1000
• Determine el incremento en el costo cuando el número de unidades se incrementa
de 50 a 60.
• Debemos calcular ΔC= C2- C1
Hallamos C1, hacemos x=50
C1=0.001(50)
3-0.3(50)
2+40(50)+1000
C1=125-750+2000+1000=2350
• Hallamos C2, hacemos x=60
C2=0.001(60)
3-0.3(60)
2+40(60)+1000
C2=216-1080+2400+1000=2536
• Remplazando en: ΔC= C2- C1 = 2536 -2350 = 186
• Si las unidades se incrementan de 50 a 60 el costo de producción se incrementa en
186 Unidades monetarias
• Interpretación geométrica de incremento
• Si el incremento de la variable dependiente “y” es negativo indica que la gráfica decrece en el intervalo X1 a X2, y si da positivo la
gráfica crece en este intervalo.

7. Razón de cambio
• Comenzando por la Razón Instantánea de Cambio de
una función cuya variable independiente es el tiempo
t. suponiendo que Q es una cantidad que varía con
respecto del tiempo t, escribiendo Q=f(t), siendo el
valor de Q en el instante t. La Razón de Cambio
Promedio de Q (por la unidad de tiempo) es, por
definición, la razón de cambio "Q en Q con respecto
del cambio "t en t, por lo que es el cociente.
Definimos la razón de cambio instantánea de Q (por
unidad de tiempo) como el límite de esta razón
promedio cuando "t!0. Es decir, la razón de cambio
instantánea de Q es

8. Conceptos

11. Ejemplos
Calcule la tasa de cambio promedio de cada función en el intervalo
dado
Remplazado en:
Es decir que la tasa de cambio promedio de y respecto a x
cuando x=2 y su incremento 0.5 es igual a -5.1

12. PROBLEMA
• El índice de precios al consumidor (IPC) de una economía
está dado por la función
donde t=0 corresponde a 1991. Calcular la tasa de cambio promedio del IPC entre 1992 y
1993. Inicialmente debemos hallar Para 1992, t=1 y en el 1993 t=2
es decir que
Remplazando en
Es decir que la tasa de cambio del índice de precios al consumidor entre 1992 y 1993 tuvieron una
tasa de cambio promedio de 1.6.

13. Limites
• un límite es una magnitud a la que
se acercan progresivamente los
términos de una secuencia infinita
de magnitudes. Un límite
matemático, por lo tanto, expresa
la tendencia de una función o de
una sucesión mientras sus
parámetros se aproximan a un
cierto valor
• .

14. Análisis
grafico de
los limites

15. Análisis
matemático
de un limite