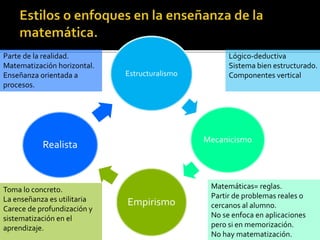
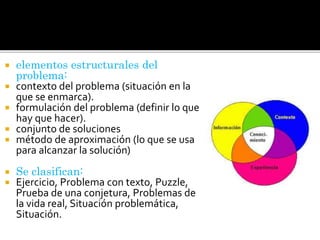
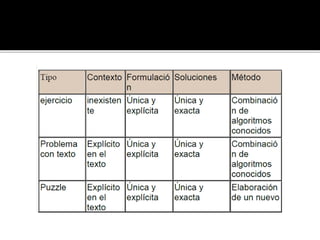
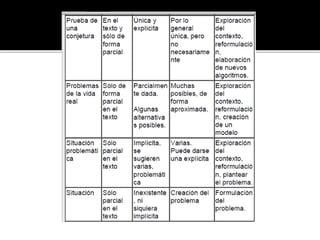
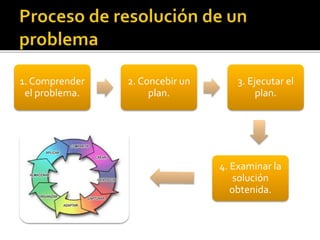
Este documento trata sobre diferentes temas relacionados con la didáctica de las matemáticas, incluyendo definiciones, enfoques, teorías de aprendizaje y resolución de problemas. Se discuten las perspectivas de Steiner, Piaget y Brousseau sobre la didáctica, así como los enfoques conductista, cognitivo y constructivista del aprendizaje. También se describen los procesos de resolución de problemas según Polya y diferentes obstáculos en la enseñanza de las matemáticas.

2. Didáctica
organización
de los procesos
de
Eseñ-Aprend
se interesa por la
producción y
comunicación del
conocimiento.
Freudenthal Brousseau
DEFINICIONES DE
DIDÁCTICA:

3.  Steiner considera que la didáctica de la
matemática debe tender hacia lo que Piaget
denominó transdisciplinariedad.
 Apoyándose en: Psicología, Pedagogía,
Sociología entre otras sin olvidar a la propia
Matemática como disciplina científica.

4. 1) EL IDEALISTA
 que se inclina por potenciar
la comprensión mediante
una visión amplia de la
matemática.
2)Y EL PRÁCTICO
 que clama por el
restablecimiento de las
técnicas básicas en interés
de la eficiencia y economía
en el aprendizaje

5.  Bases filosóficas se encuentran en: Seminario de Royamount, 1959.
 Jean Diudonné : enseñanza basada en el carácter deductivo de la
matemática.
 A finales de los sesenta y principios de los setenta, la nueva
matemática ha sido un fracaso, pues no se aprenden los conceptos ni
las estructuras superiores.
 Retorno a lo básico, retomar la práctica de los algoritmos y
procedimientos. Pero, los alumnos, en el mejor de los casos,
aprendían de memoria los procedimientos sin comprenderlos.

6.  La Matematización.
 Matematizar es organizar y estructurar la información que
aparece en un problema, identificar los aspectos
matemáticos relevantes, descubrir regularidades,
relaciones y estructuras.

7.  HORIZONTAL, no lleva
del mundo real al
mundo de los símbolos
y posibilita tratar
matemáticamente un
conjunto de
problemas.
 Procesos que se
utilizan

8.  VERTICAL, consiste en
el tratamiento
específicamente
matemático de las
situaciones, y en tal
actividad son
característicos los
siguientes procesos:
 Procesos que se
utilizan

9. Estructuralismo
Mecanicismo
Empirismo
Realista
Lógico-deductiva
Sistema bien estructurado.
Componentes vertical
Matemáticas= reglas.
Partir de problemas reales o
cercanos al alumno.
No se enfoca en aplicaciones
pero si en memorización.
No hay matematización.
Toma lo concreto.
La enseñanza es utilitaria
Carece de profundización y
sistematización en el
aprendizaje.
Parte de la realidad.
Matematización horizontal.
Enseñanza orientada a
procesos.

10.  ¿Qué es un problema?
 significa buscar una acción apropiada para lograr
un objetivo claramente concebido pero no
alcanzable de forma inmediata.
 tres requisitos:
 1) Aceptación: aceptar el problema
 2) Bloqueo: Los intentos iniciales no dan fruto.
 3) Exploración: de nuevos métodos para atacar
el problema.

11.  R. Borasi (1986), en uno de los primeros
intentos en clarificar la noción de problema
originada por su interés en mejorar la
enseñanza de la resolución de problemas,
utiliza los siguientes elementos estructurales
para una tipología de problemas:

12.  elementos estructurales del
problema:
 contexto del problema (situación en la
que se enmarca).
 formulación del problema (definir lo que
hay que hacer).
 conjunto de soluciones
 método de aproximación (lo que se usa
para alcanzar la solución)
 Se clasifican:
 Ejercicio, Problema con texto, Puzzle,
Prueba de una conjetura, Problemas de
la vida real, Situación problemática,
Situación.

15. 1. Comprender
el problema.
2. Concebir un
plan.
3. Ejecutar el
plan.
4. Examinar la
solución
obtenida.

16.  Lo que usamos al solucionar un problema:
 Recursos congnitivos: conjunto de hechos y
procedimientos a disposición del resolutor.
 Heurísticas: reglas para progresar en situaciones
dificultosas.
 Control: Aquello que permite un uso eficiente de
los recursos disponibles.
 Sistema de creencias: Nuestra perspectiva con
respecto a la naturaleza de la matemática y
como trabajar en ella.

17.  Inflexibilidad para considerar alternativas. (Salir
del bloqueo).
 Rigidez en la ejecución de procedimientos.
 Querer utilizar un procedimiento donde no es
aplicable.
 Incapacidad de anticipar las consecuencias de
una acción. (Qué consecuencias traera la
acción que ponga en práctica).
 El efecto "túnel". No hay energías para la
evaluación.

18.  La finalidad de tal modelo es que la persona examine
y remodele sus propios métodos de pensamiento de
forma sistemática a fin de eliminar obstáculos y de
llegar a establecer hábitos mentales eficaces.
 Lo que Polya denominó como pensamiento
productivo.
 Familiarízate con el problema
 Búsqueda de estrategias
 Lleva adelante tu estrategia
 Revisa el proceso y saca consecuencias de él

19.  ¿¿Qué ES??...
 El enfoque en la resolución de problemas.
 Enseñar para resolver problemas
▪ Proponer problemas, que sean aplicables a la vida diaria,
problemas y no solo ejercicios, que promuevan la
investigación.
 Enseñar sobre la resolución de problemas.
▪ Enseñanza sobre la Heurística (que es el arte de inventar o
descubrir). Propone que los Alumnos utilicen estrategias.
 Enseñar vía la resolución de problemas.
Desarrollo de la capacidad de razonamiento.

20.  Énfasis en enseñar procedimientos. Se presta poca
atención a ayudar a los alumnos a desarrollar ideas
conceptuales, o incluso a conectar los procedimientos.
 Curriculum de USA, no propone problema retadores.
 En la secundaria se trabaja con la actividad que consiste en
la explicación del contenido por el profesor, trabajo
individual de los alumnos sobre las tareas propuestas y
corrección de las mismas.
 Los maestros y los profesores enseñan de la misma forma
en que fueron enseñados en la escuela.

21.  Nuestras creencias sobre qué es matemática influye en la
forma en que la enseñamos.Y pueden ser un obstáculo.
 Los profesores que ven su tarea como la transmisión de un
conocimiento acabado y abstracto tienden a adoptar un
estilo expositivo. (MECANISMO o CONDUCTISMO)
 Donde el alumno es como un ordenador y puede ser
programado por la practica repetitiva

22.  Si creemos que el conocimiento matemático no son
conceptos que se aprenden y que existen estructuras
conceptuales que amplían y enriquecen a lo largo de toda
la vida, entonces ya no bastará con la exposición.
 Habrá que hacer partícipe a los alumnos del propio
aprendizaje. Y sólo hay una forma de hacer partícipe a
los alumnos: dar significado a todo lo que se enseña.

23.  No matar el interés del alumno con ejercicios rutinarios.
 Poner a prueba la curiosidad
 Plantearles problemas y preguntas estimulantes
 Despertar el pensamiento independiente
 Darles recursos para que lo logren

24.  asociacionismo, cuya recomendación
pedagógica más simple era la práctica
educativa de ejercicios bien secuenciados. No
se prestó ningún interés en explorar las
estructuras cognitivas del individuo.
 Una metodología de investigación: el
paradigma agrícola

25.  El asociacionismo deThorndike.
 aprendizaje activo y selectivo de respuestas
satisfactorias. el conocimiento incluso el más
complejo esta formado por relaciones sencillas,
vínculos entre estímulos y respuestas.
 los programas para enseñar matemáticas podrían
elaborarse sobre la base de estímulos y
respuestas sucesivos, el resultado se vería
reflejado en la conducta de los alumnos

26.  El aprendizaje sencillo facilitaba el más complejo.
 El problema central aquí es la transferencia desde un aprendizaje a
otro.
 Thorndike sugirió que tal transferencia podría ocurrir siempre que
ambas tareas contuviesen elementos comunes.
 Roberto Gagne. Mencionaba que las tareas
más sencillas funcionan como elementos de
las más complejas.
 jerarquía del aprendizaje permite plantear
objetivos perfectamente secuenciados desde
 una lógica disciplinar.

27.  La práctica educativa se centra, por lo tanto,
en la ejecución y repetición de determinados
ejercicios secuenciados, en pequeños pasos,
que deben ser realizados individualmente y
que más tarde se combinan con otros
formando grandes unidades de competencia
para el desarrollo de cierta habilidad
matemática.
 existe poco o nulo interés en explorar las
estructuras y los procesos cognitivos.

28.  La cognición no comienza con los conceptos,
sino todo lo contrario, los conceptos son el
resultado del proceso cognitivo (Freudenthal
1991, p.18)
 El problema central de la ciencia cognitiva es
la construcción de los conceptos por los
individuos.

29.  Piaget denominó epistemología
genética a su teoría sobre la
construcción del conocimiento
por los individuos (Piaget, 1987;
García, 1997).
 equilibración se lleva a cabo
mediante dos procesos,
íntimamente relacionados y
dependientes, que son la
asimilación y la acomodación.

30.  Toda la información es procesada por una
serie de memorias, que procean y almacenan
de forma distinta y que además están sujetas
a determinadas limitaciones en su función.
 La información entra en el sistema a través de
un registro de entrada sensorial,
 Por último, se encuentra la memoria a largo
plazo o semántica.