Distribución normal

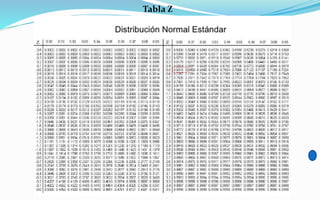
La distribución normal
Reconocida por primera vez por Abraham
Moivre.
Posteriormente fue Carl Friedrich Gauss
(1777-1855) quien profundizó sus estudios ,
formulando la ecuación de la curva
conocida comúnmente, como la campana
de Gauss.
ronald.mayhuasca.s@upch.pe

Utilidad
En muchas variables asociadas a fenómenos naturales que siguen el
modelo de la curva normal.
•Caracteres morfológicos de individuos: talla, pesos, diámetros,
distancias, perímetros, etc.
•Caracteres fisiológicos, como efectos de a dosis de un fármaco, o
de una misma cantidad de inhibidor, flúor.
•Caracteres sociológicos, por ejemplo: consumo de cierto
producto por un mismo grupo de individuos, puntuaciones de
examen.

Utilidad
En muchas variables asociadas a fenómenos naturales que siguen el
modelo de la curva normal.
•Caracteres psicológicos, ejemplo: cociente intelectual, grado de
adaptación a un medio,…
•En estadística: errores cometidos al medir ciertas magnitudes,
valores estadísticos muestrales como la media, varianza y moda.

La función de distribución
•Puede tomar cualquier valor ( - ∞, + ∞)
•Hay más probabilidad para los valores cercanos a la media (µ).
•Conforme nos separamos de µ, la probabilidad va decreciendo de
igual forma a derecha e izquierda (es simétrica respeto a la media).
•Conforme nos separamos de µ, la probabilidad va decreciendo
dependiendo de la desviación estándar (σ)
µ

Propiedades de la distribución normal
•La forma de la campana de Gauss depende de los parámetros µ y σ.
•La media, mediana y moda son iguales.
•La curva normal es asintótica al eje de X.
•Es simétrica con respecto a su media µ, es decir el área que
corresponde a la mitad de la curva es igual a 0.50, o sea la probabilidad
de que X< µ, o de que X> µ, es 0.50.

La desviación estándar (σ)
Distribuciones normales con distintas desviaciones estándar e igual media.

La media (µ)
Distribuciones normales con distintas desviaciones estándar e igual media.

Resumen
•Podemos decir que hay un conjunto de distribuciones con una forma
común, diferenciadas por los valores de su media y su varianza.
•La desviación estándar (σ) determina el grado de apuntamiento de la
curva. A mayor la σ, más se dispersarán los datos en torno a la media y la
curva será más plana.
•La media indica la posición de la campana , de modo que para diferentes
valores de la µ, la gráfica es desplazada a lo largo del eje horizontal.
•De entre todas, la más usada es la distribución normal estándar, que
corresponde a una distribución de media 0 y varianza 1.

La distribución normal estándar (z)
•A z se le denomina función tipificada de x, y
a la curva de su función de densidad se le
conoce como la curva normal estándar.
•Es una distribución normal con promedio 0
y una desviación estándar de 1.
•Todas las variables que se distribuyen
normalmente se pueden transformar a la
distribución normal estándar utilizando la
fórmula para calcular el valor Z y ver en la
tabla Z.

Características de la distribución normal estándar
•Su media es 0, su varianza y desviación estándar es 1
•La curva f(z) es simétrica respecto al eje de Z.
•La media, mediana y moda es 0.

Área bajo la curva normal estándar
•El área bajo la curva normal estándar es útil para
asignar probabilidades de ocurrencia de la variable X.
•Debemos tomar en cuenta que el área total bajo la
curva es igual a 1, por ser una gráfica simétrica cada
mitad tiene un área de 0.5.

Pasos para determinar el área bajo la curva
normal estándar
•Paso 1: interpretar gráficamente el área de interés
•Paso 2: Determinar el valor de Z.
•Paso 3: Buscar en la tabla de probabilidades
•Paso 4: Hacer la suma o resta de áreas para encontrar la
probabilidad deseada.

Ejemplos y ejercicios
SECCIÓN
Supongamos que sabemos que el peso de los
estudiantes universitarios sigue una distribución
aproximadamente normal, con una media de 70kg y
una desviación estándar de 10kg.
µ=70kg
σ=10kg

Ejemplo 01
Determine la probabilidad de que una persona tenga un peso
menor o igual a 75kg.
Paso 01: Interpretar gráficamente el área de interés.
Gráficamente si decimos que a=75kg, el área de la curva
que nos interesa es la siguiente:
75kg

Paso 02: Determine el valor de Z:
Z=(x-µ)/σ = (75-70)/10 =0.50
Paso 03: Buscar en la tabla de probabilidades.
Buscamos en la tabla. El valor Z=0.50 y obtenemos el área
de 0.6915

Paso 04: Hacer la suma o resta de áreas para encontrar la
En este ejemplo no es necesario realizar la resta a 1, ya que
el área es la misma que se representa en la tabla . Por lo
tano la probabilidad de que X<75 es igual a 0.6915. (En
porcentaje sería el 69,15%)

Ejemplo 02
Si deseamos la probabilidad de que una persona elegida al azar ,
tenga un peso mayor a 75kg.
75kg ronald.mayhuasca.s@upch.pe

mayor a 75kg.
Z=(x-µ)/σ = (75-70)/10 =0.50
Buscamos en la tabla. El valor Z=0.50 y obtenemos el área
de 0.6915 (obtenido en la en el ejemplo 01, pero no es el
área que nos piden).

mayor a 75kg.
En este ejemplo el área 0,6915 no es el área que nos
interesa por tanto restamos a 1 y el resultado será igual a
0,3085. (En porcentaje sería el 30,85%)

Ejemplo 03
Determine la probabilidad de que una persona elegida al azar
tenga un peso menor a 55kg.
55kg
70kg
75kg

Z=(x-µ)/σ = (55-70)/10 =-1.50
Buscamos en la tabla. El valor Z=-1.50 y obtenemos el área
de 0.0668

En este ejemplo el área 0,0668 es el área que nos interesa
por tanto es la probabilidad deseada. (En porcentaje sería
el 6,68%)

Ejemplo 04
Determine la probabilidad de que una persona elegida al azar
tenga un peso entre 55 y 75 kg.
75kg55kg

Ejercicio:
Para la distribución normal tipificada , media 0, varianza 1.
calcular:
• Percentil 28
• RIQ: Q3 – Q1

Distribución normal

Más contenido relacionado

La actualidad más candente

Similar a Distribución normal

Más de Univ Peruana Los Andes

Último

Distribución normal