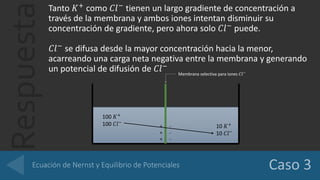
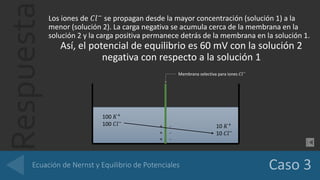
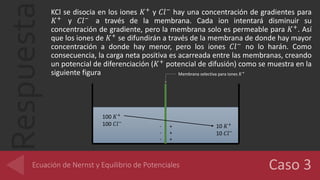
El documento analiza el potencial de diferenciación a través de membranas selectivas para iones K+, Cl-, y Ca2+, utilizando la ecuación de Nernst para calcular los potenciales de equilibrio. Se detalla cómo la acumulación de cargas en las membranas genera un potencial que compensa el gradiente de concentración, logrando equilibrio electroquímico sin modificar las concentraciones de los iones en las soluciones. Además, se evalúa la conductancia de una fibra nerviosa, determinando que Cl- es el ion con mayor permeabilidad, seguido por K+ y Na+.

1. Caso 3: Ecuación de Nernst y
Equilibrio de Potenciales

2. Pregunta Una solución de 100 mmol/L de KCl es separada de una
solución de 10 mmol/L de KCl por una membrana
permeable a iones 𝐾+, pero impermeable a iones 𝐶𝑙−.
¿Cuál es la magnitud y dirección del potencial de
diferenciación que se generará a través de esta
membrana?
Asume que 2.3 RT/F = 60 mV
¿Cambiará la concentración de 𝐾+
en alguna de las
soluciones como resultado del proceso que genera
este potencial de diferenciación?

3. Respuesta
KCl se disocia en los iones 𝐾+ y 𝐶𝑙− hay una concentración de gradientes para
𝐾+ y 𝐶𝑙− a través de la membrana. Cada ion intentará disminuir su
concentración de gradiente, pero la membrana solo es permeable para 𝐾+. Así
que los iones de 𝐾+ se difundirán a través de la membrana de donde hay mayor
concentración a donde hay menor, pero los iones 𝐶𝑙− no lo harán. Como
consecuencia, la carga neta positiva es acarreada entre las membranas, creando
un potencial de diferenciación (𝐾+ potencial de difusión) como se muestra en la
siguiente figura Membrana selectiva para iones 𝐾+
10 𝐾+
10 𝐶𝑙−
100 𝐾+
100 𝐶𝑙−
-
-
-
+
+
+

4. Respuesta La acumulación de carga positiva en la membrana retrasa la difusión
de 𝐾+ (la carga positiva repele la carga positiva). Eventualmente,
suficiente carga positiva se acumula en la membrana para
compensar la tendencia de 𝐾+ para difundir su gradiente de
concentración. Esta condición, llamada equilibrio electroquímico,
ocurre cuando las fuerzas químicas y la eléctricas en un ion (en este
caso 𝐾+
) son iguales y contrarias y no ocurre más difusión neta de
iones.

5. Respuesta Se necesitan pocos iones de 𝐾+
para establecer el
equilibrio electroquímico porque muy pocos iones
están involucrados y el proceso no cambia el
gradiente de concentración de 𝐾+
en las soluciones.
Se indica otra, debido a la rápida generación del
potencial de difusión de 𝐾+
, 𝐾+
no se difunde hasta
que las dos soluciones tengan concentraciones
iguales de 𝐾+
(como ocurriría con la difusión de un
soluto sin carga).

6. Respuesta La ecuación de Nernst se utiliza para calcular la magnitud
del potencial de diferenciación generado por la difusión
de un solo ion permanente (en este caso, 𝐾+
). Así, la
ecuación de Nernst se usa para calcular el potencial de
equilibrio de un ion por una diferencia de concentración a
través de la membrana, asumiendo que la membrana es
permeable solo a ese ion.
𝐸 = −
2.3 𝑅𝑇
𝑧 𝐹
𝑙𝑜𝑔10
[𝐶1]
[𝐶2]

7. Respuesta 𝐸 = −
2.3 𝑅𝑇
𝑧 𝐹
𝑙𝑜𝑔10
[𝐶1]
[𝐶2]
Donde:
E = potencial de equilibrio (mV)
2.3 RT/F = constantes (60 mV a 37°C)
z = carga del ion (incluyendo el signo)
𝐶1 = concentración del ion en una solución (mmol/L)
𝐶2 = concentración del ion en la otra solución (mmol/L)

8. Respuesta Ahora, contestando a la pregunta
“¿Cuál es la magnitud y la dirección del potencial de
diferenciación que es generado por la difusión de los
iones de 𝐾+
abajo de un gradiente de concentración
de esta magnitud?”
Puesto de otra manera: ¿Cuál es el potencial de
equilibrio de 𝐾+
para esta diferencia de
concentración?

9. RespuestaEn práctica, los cálculos de la ecuación de Nernst pueden ser
aerodinámicos. Porque estos problemas involucran funciones
logarítmicas, todos los signos en la calculación pueden ser omitidos, y
la ecuación ser resuelta por el valor absoluto del potencial de
diferenciación.
Por conveniencia, siempre ponemos la mayor concentración en el
numerador y la de menor concentración en el denominador. El signo
correcto del potencial de diferenciación es determinado después por
intuición, como se muestra en el siguiente ejemplo

10. RespuestaLa mayor concentración de 𝐾+
es 100 mmol/L, la menor es e
10 mmol/L
2.3 RT/F es 60 mV a 37°C
z para 𝐾+
es +1
Como estamos determinando el potencial de equilibrio de
𝐾+
, “E” se denota como 𝐸 𝐾+
Recuerda que acordamos omitir todos los signos en el cálculo
para determinarlo al final por intuición.
𝐸 𝐾+ =
60 𝑚𝑉
1
𝑙𝑜𝑔10
100 𝑚𝑚𝑜𝑙/𝐿
10 𝑚𝑚𝑜𝑙/𝐿

11. Respuesta 𝐸 𝐾+ =
60 𝑚𝑉
1
𝑙𝑜𝑔10
100 𝑚𝑚𝑜𝑙/𝐿
10 𝑚𝑚𝑜𝑙/𝐿
𝐸 𝐾+ = 60 𝑚𝑉 × 𝑙𝑜𝑔1010
𝐸 𝐾+ = 60 𝑚𝑉 × 1
𝐸 𝐾+ = 60 𝑚𝑉
Valor absoluto del potencial de equilibrio

12. Respuesta¿A dónde se difusa 𝐾+ para crear su potencial de diferenciación?
Se difusa desde la mayor concentración (solución 1) a la menor concentración
(solución 2). Las cargas positivas se acumulan cerca de la membrana en la
solución 2, las cargas negativas se quedan detrás de la membrana en la solución
1. Así, el potencial de diferenciación (o el potencial de equilibrio de 𝐾+) es 60 mV,
con la solución 1 negativa con respecto a
la solución 2.
O puesto de otra manera, el potencial
de diferenciación es 60 mV, con la
solución 2 positiva con respecto a la 1

13. PreguntaSi las mismas soluciones antes descritas ahora son
separadas por una membrana permeable a iones 𝐶𝑙−, pero
impermeable a iones 𝐾+
¿Cuál es la magnitud y el sentido del potencial
de diferenciación que se genera en la
membrana?

14. Respuesta
Tanto 𝐾+
como 𝐶𝑙−
tienen un largo gradiente de concentración a
través de la membrana y ambos iones intentan disminuir su
concentración de gradiente, pero ahora solo 𝐶𝑙−
puede.
𝐶𝑙−
se difusa desde la mayor concentración hacia la menor,
acarreando una carga neta negativa entre la membrana y generando
un potencial de difusión de 𝐶𝑙−
100 𝐾+
100 𝐶𝑙−
10 𝐾+
10 𝐶𝑙−
+
+
+
-
-
-
Membrana selectiva para iones 𝐶𝑙−

15. Respuesta
Conforme la carga negativa se acumula en la
membrana se retrasa la difusión de 𝐶𝑙−
(negativo
repele negativo). En el equilibrio electroquímico, la
tendencia del 𝐶𝑙−
de disminuir su gradiente de
concentración es compensada por el potencial de
diferenciación que se genera.
En otras palabras, las fuerzas químicas y eléctricas
de 𝐶𝑙−
son iguales y contrarias. De nuevo, se
necesitan pocos iones de 𝐶𝑙−
difusos para crear el
potencial de diferenciación por lo que no cambia la
concentración de 𝐶𝑙−
en las soluciones.

16. Respuesta
Ahora calcularemos el potencial de equilibrio de 𝐶𝑙−
con las mismas especificaciones de la pregunta
anterior.
𝐸 𝐶𝑙− =
60 𝑚𝑉
1
𝑙𝑜𝑔10
100 𝑚𝑚𝑜𝑙/𝐿
10 𝑚𝑚𝑜𝑙/𝐿
𝐸 𝐶𝑙− = 60 𝑚𝑉 × 𝑙𝑜𝑔1010
𝐸 𝐶𝑙− = 60 𝑚𝑉 × 1
𝐸 𝐶𝑙− = 60 𝑚𝑉
Valor absoluto del potencial de equilibrio

17. RespuestaLos iones de 𝐶𝑙− se propagan desde la mayor concentración (solución 1) a la
menor (solución 2). La carga negativa se acumula cerca de la membrana en la
solución 2 y la carga positiva permanece detrás de la membrana en la solución 1.
Así, el potencial de equilibrio es 60 mV con la solución 2
negativa con respecto a la solución 1
100 𝐾+
100 𝐶𝑙−
10 𝐾+
10 𝐶𝑙−
+
+
+
-
-
-
Membrana selectiva para iones 𝐶𝑙−

18. PreguntaUna solución de 5 mmol/L de 𝐶𝑎𝐶𝑙2 es separada de
una solución de 1 𝜇 mol/L de 𝐶𝑎𝐶𝑙2 por una
membrana que es semipermeable a 𝐶𝑎2+
, pero es
impermeable a 𝐶𝑙−
¿Cuál es la magnitud y el sentido del potencial de
diferencia que es generado a través de la
membrana?

19. Respuesta Tenemos un gradiente de concentración para 𝐶𝑎𝐶𝑙2
a través de la membrana que es semipermeable a
iones de 𝐶𝑎2+
. Te piden que calcules el potencial de
equilibrio de 𝐶𝑎2+
del gradiente de concentración
fijado (por ejemplo, el potencial de diferenciación
que compensaría la tendencia de 𝐶𝑎2+
de disminuir
su gradiente de concentración).
Los iones de 𝐶𝑎2+
se propagan desde la mayor
concentración hacia la de menor y cada ión acarrea
2 cargas positivas.
Ecuación de Nernst y Equilibrio de Potenciales

20. Respuesta
Calcularemos el potencial de equilibrio de 𝐶𝑎2+
con
las mismas especificaciones pero recordando que
para 𝐶𝑎2+
“z” es +2
𝐸 𝐶𝑎2+ =
60 𝑚𝑉
2
𝑙𝑜𝑔10
5 𝑚𝑚𝑜𝑙/𝐿
1 𝜇𝑚𝑜𝑙/𝐿
𝐸 𝐶𝑎2+ = 30 𝑚𝑉 × 𝑙𝑜𝑔10
5 × 10−3 𝑚𝑜𝑙/𝐿
1 × 10−6 𝑚𝑜𝑙/𝐿
𝐸 𝐶𝑎2+ = 30 𝑚𝑉 × 𝑙𝑜𝑔105 × 103
𝐸 𝐶𝑎2+ = 30 𝑚𝑉 × 3.699
𝐸 𝐶𝑎2+ = 111 mV
Ecuación de Nernst y Equilibrio de Potenciales

21. Respuesta
𝐶𝑎2+ se propaga de la solución de mayor concentración
(solución 1) a la de menor (solución 2) acarrando cargas
positivas a través de la membrana y dejando las negativas
atrás. Así, el potencial de equilibrio para 𝐶𝑎2+ es 111 mV,
con Solución 1 negativa con respecto a Solución 2
Ecuación de Nernst y Equilibrio de Potenciales
𝐶𝑎2+
𝐶𝑙−
𝐶𝑎2+
𝐶𝑙−
Membrana selectiva para iones 𝐶𝑎2+
-
-
-
+
+
+

22. Pregunta
Una fibra nerviosa es colocada en una solución de composición similar al
líquido extracelular. Después de prepararla a 37°C, un microelectrodo es
insertado en la fibra nerviosa para grabar el potencial de diferencia desde la
membrana nerviosa a 70 mV, siendo el interior negativo con respecto a la
solución. La composición del líquido intracelular y el líquido extracelular (en
este caso la solución) se muestra en la siguiente tabla:
Asumiendo que 2.3 RT/F = 60 mV a 37°C
¿Cuál ion está más cerca del equilibrio electroquímico?
¿Qué podemos concluir de la relativa conductancia de la membrana del nervio
para el 𝑁𝑎+, 𝐾+ y 𝐶𝑙− en estas condiciones?
Ion Intracelular Extracelular
𝑁𝑎+ 30 mmol/L 140 mmol/L
𝐾+ 100 mmol/L 4 mmol/L
𝐶𝑙− 5 mmol/L 100 mmol/L

23. Respuesta El problema nos da las concentraciones intra y
extracelulares de 𝑁𝑎+
, 𝐾+
y 𝐶𝑙−
, así como el
potencial de membrana de la fibra nerviosa. La
pregunta aquí es cuál ion es el más cercano al
equilibrio electroquímico en estas circunstancias.
Indirectamente te están preguntando qué ión tiene
la permeabilidad o conductancia más alta en la
membrana.

24. Respuesta La idea es primero calcular el potencial de equilibrio para
cada ion con la gradiente de concentración.
𝐸 𝑁𝑎+ =
60 𝑚𝑉
1
𝑙𝑜𝑔10
140 𝑚𝑚𝑜𝑙/𝐿
30 𝑚𝑚𝑜𝑙/𝐿
𝐸 𝑁𝑎+ = 60 𝑚𝑉 × 𝑙𝑜𝑔104.67
𝐸 𝑁𝑎+ = 60 𝑚𝑉 × 0.669
𝐸 𝑁𝑎+ = 40 𝑚𝑉
(+40 mV ya que en el interior de la célula es positivo)

25. Respuesta 𝐸 𝐾+ =
60 𝑚𝑉
1
𝑙𝑜𝑔10
100 𝑚𝑚𝑜𝑙/𝐿
4 𝑚𝑚𝑜𝑙/𝐿
𝐸 𝐾+ = 60 𝑚𝑉 × 𝑙𝑜𝑔1025
𝐸 𝐾+ = 60 𝑚𝑉 × 1.40
𝐸 𝐾+ = 84 𝑚𝑉
(-84 mV ya que en el interior de la célula es negativo)

26. Respuesta 𝐸 𝐶𝑙− =
60 𝑚𝑉
1
𝑙𝑜𝑔10
100 𝑚𝑚𝑜𝑙/𝐿
5 𝑚𝑚𝑜𝑙/𝐿
𝐸 𝐶𝑙− = 60 𝑚𝑉 × 𝑙𝑜𝑔1020
𝐸 𝐶𝑙− = 60 𝑚𝑉 × 1.3
𝐸 𝐶𝑙− = 78 𝑚𝑉
(-78 mV ya que en el interior de la célula es negativo)

27. Respuesta
Ahora compara los potenciales de equilibrio calculados con el
potencial de membrana.
𝐸 𝑁𝑎+ = 40 𝑚𝑉
𝐸 𝐾+ = 84 𝑚𝑉
𝐸 𝐶𝑙− = 78 𝑚𝑉
𝐸 = 70 𝑚𝑉
Si el potencial de equilibrio calculado de un ion es cercano o
igual al que la membrana, entonces ese es el más cercano al
equilibrio electroquímico, por lo que debe tener la mayor
permeabilidad o conductancia.

28. RespuestaLa siguiente figura muestra las concentraciones de los 3 iones en el líquido
intracelular y extracelular de la fibra nerviosa. Es importante saber que los
potenciales de membrana y potenciales del equilibrio siempre están
expresados como potencial intracelular con respecto al potencial extracelular.
Por ejemplo, en este ejemplo la membrana potencial es 70 mV, el interior de la
célula es negativo así que es -70 mV
Líquido intracelular
Líquido extracelular
30 𝑁𝑎+
100 𝐾+
5 𝐶𝑙−
140 𝑁𝑎+
4 𝐾+
100 𝐶𝑙−
- - -
+ + +
- - -
+ + +
+ + +
- - -

29. Respuesta Por lo anterior:
𝐶𝑙−
es el ion con mayor
conductancia/permeabilidad, seguido por 𝐾+
y
finalmente 𝑁𝑎+
con muy poca
conductancia/permeabilidad