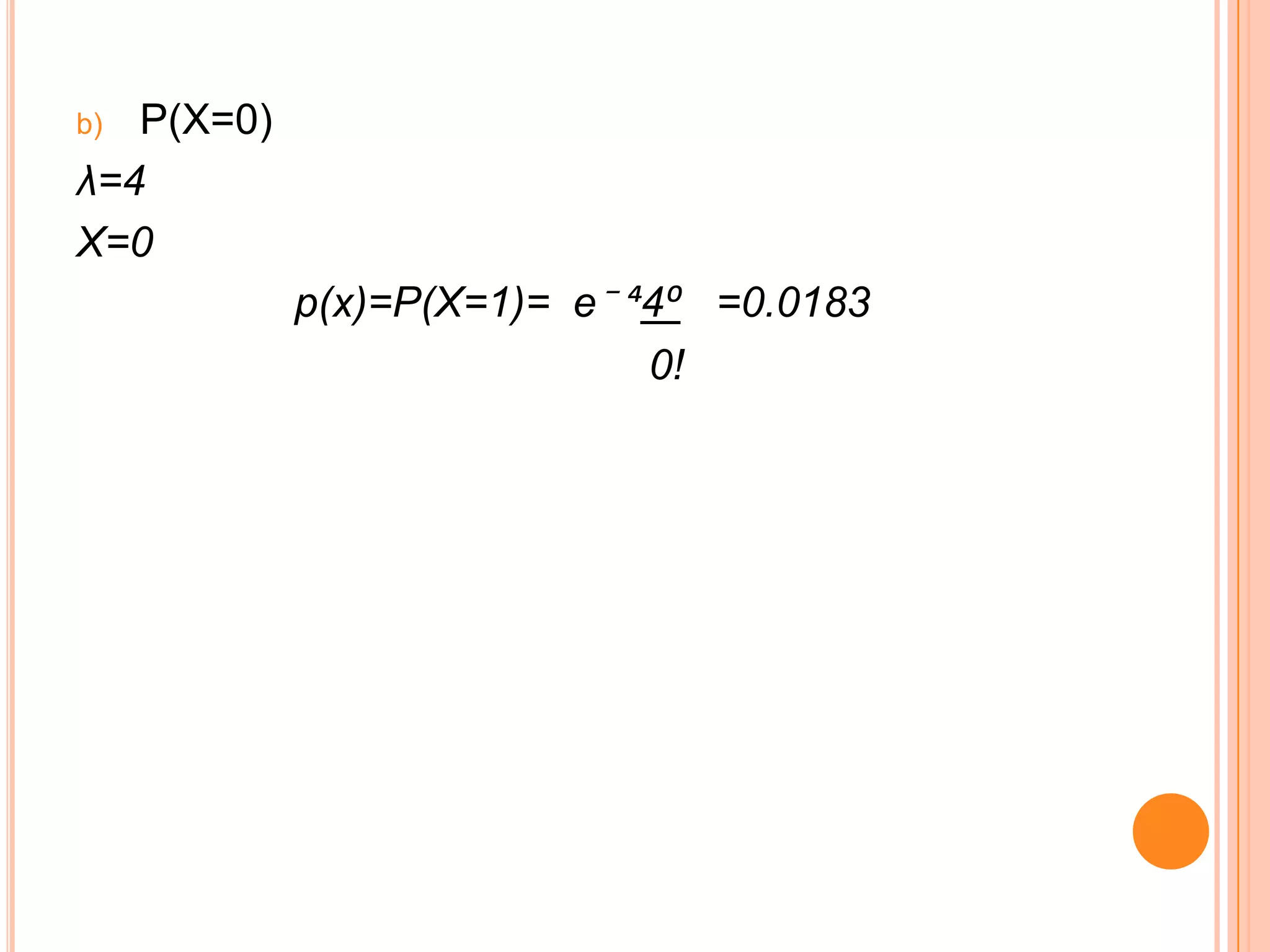El documento presenta varios problemas estadísticos relacionados con distribuciones de probabilidad. En el primer problema, se calculan la media y varianza de una variable aleatoria con distribución de Bernoulli. En el segundo problema, se calculan la media y varianza de una variable aleatoria con distribución binomial. En el tercer problema, se calculan probabilidades para una variable aleatoria con distribución de Poisson.

2. DISTRIBUCIÓN BERNOULLI
Un jugador de básquetbol esta a punto de tirar hacia la parte
superior del tablero. La probabilidad de que anote el tiro es de
0.55.
a) Sea X=1 si anota el tiro, si no lo hace X=0 determine la
media y la varianza de X.
b) Si anota el tiro su equipo obtiene 2 puntos. Si lo falla su
equipo no recibe puntos. Sea Y el numero de puntos
anotados ¿tiene una distribución de Bernoulli? Si es así
encuentre la probabilidad de éxito, si no explique porque.
c) Determine la medida y varianza de Y

3. a) Sea X=1 si anota el tiro, si no lo hace X=0 determine la media y la
varianza de X.
Lo primer que tenemos que determinar son los valores de X que es igual a
los eventos que son 1 y 0. Y la probabilidad, la cual es que si anota es de
0.55 y si no lo hace es de 0.45
Eventos probabilidades
X=1 si anota 1 0.55
X=0 si no anota 0 0.45
Para determinar la media se multiplica el numero de eventos por la
probabilidad. Después sumamos ambos resultados de dichas
multiplicaciones y esto nos dará la media
(p)= 1(0.55)= 0.55
(1-p)=0(0.45)=__0__
Media= 0.55
Para obtener nuestra varianza le restaremos nuestro numero de evento la
media que obtuvimos y esto lo elevaremos al cuadrado y después lo
multiplicaremos por la probabilidad. Y ambos resultados obtenidos se
sumaran y esto nos dará a nuestra varianza.
(1-0.55)²(0.55)=0.1111375
(0-0.55)²(0.45)=0.1361255
Varianza=0.2475

4. b) Si anota el tiro su equipo obtiene 2 puntos. Si lo falla su equipo no
recibe puntos. Sea Y el numero de puntos anotados ¿tiene una
distribución de Bernoulli? Si es así encuentre la probabilidad de
éxito, si no explique porque.
Para determinar si es o no una distribución Bernoulli devemos obtener
nuevamente los valores de los eventos que en este caso se representan
con una Y, y son 2 y 0. y las probabilidades son iguales ya que estamos
hablando de el mismo acontecimiento.
Eventos probabilidades
Y=2 si anota 2 0.55 (p)= 2(0.55)= 1.1
Y=0 si no anota 0 0.45 (2-p)=0(0.45)= 0
A esto podemos decir que una distribución Bernoulli ya que esta nos
especifica que si los evento no son 1 y 0 entonces esto no seria posible.
No es una distribución Bernoulli porque los eventos que se presentan no
son 1 y 0.

5. c) Determine la medida y varianza de Y
En este caso podemos aplicar la misma técnica que en el inciso a) los valores
de Y son igual a los eventos que son 2 y 0. Y la probabilidad, la cual es que si
anota es de 0.55 y si no lo hace es de 0.45
Eventos probabilidades
X=1 si anota 2 0.55
X=0 si no anota 0 0.45
Para determinar la media se multiplica el numero de eventos por la
probabilidad. Después sumamos ambos resultados de dichas multiplicaciones
y esto nos dará la media
(p)= 2(0.55)= 1.1
(1-p)=0(0.45)=__0__
Media= 1.1
Para obtener nuestra varianza le restaremos nuestro numero de evento la media
que obtuvimos y esto lo elevaremos al cuadrado y después lo multiplicaremos
por la probabilidad. Y ambos resultados obtenidos se sumaran y esto nos dará
a nuestra varianza.
(2-1.1)²(0.55)=0.4455
(0-1.1)²(0.45)=0.5445
Varianza=0.99

6. DISTRIBUCIÓN BINOMIAL
1. Se toma una muestra de 5 elementos de una población
grande en la cual el 10% de los elementos esta defectuoso.
a) Determine la probabilidad de que ninguno de los elementos
de la muestra este defectuoso.
b) Determine la probabilidad de que solo uno de ellos tenga
defectos.
c) Determine la probabilidad de que uno o más de los
elementos de la muestra estén defectuosos.
d) Determine la probabilidad de que menos de dos elementos
de la muestra tengan defectos.

7. a) Determine la probabilidad de que ninguno de los elementos de la
muestra este defectuoso.
Se dice que se toma una muestra de 5 elementos el cual el 10% esta
defectuoso y se nos pide que determinemos la probabilidad de que
ninguno de los elementos este defectuoso a lo que tenemos la
siguiente formula:
p (X=x)= n pˣ(1-p)ⁿ⁻ˣ
x
A lo cual sustituimos:
X=0
n=5
p=0.1
p(x=0)= 5 0.1⁰(1-0.1)µ⁻⁰=0.59049
0
Al hacer estas operaciones obtendremos lo siguientes
resultados:
p(x=0)=1*1*0.59049= 0.59049

8. b) Determine la probabilidad de que solo uno de ellos
tenga defectos.
Sustituimos como en el inciso pasado, pero como nuestros
valores de p y n son iguales solo lo haremos con X. ya que
solo se nos esta pidiendo la probabilidad de que solo uno
de ellos tenga defecto.
X=1
p(x=1)= 5 0.1¹(1-0.1)µ⁻¹=0.32805
1
Al hacer estas operaciones obtendremos lo siguientes
resultados:
p(x=1)= 5*0.1*0.6561 = 0.32805

9. c) Determine la probabilidad de que uno o más de los
elementos de la muestra estén defectuosos.
En este inciso como en los otros solo sustituiremos el valor de X.
p(x=3)= 5 0.1³(1-0.1)µ⁻³=0.0081
3
p(x=3)= 10*0.001*0.81= 0.0081
p(x=4)= 5 0.1´(1-0.1)µ⁻´=0.00045
4
p(x=4)= 5*0.0001*0.9= 0.00045
p(x=5)= 5 0.1µ(1-0.1)µ⁻µ=0.00001
5
p(x=5)= 1*.00001*1= 0.00001

10. d) Determine la probabilidad de que menos de dos
elementos de la muestra tengan defectos.
En este inciso como en los otros solo sustituiremos el valor
de X.
p(x=2)= 5 0.1²(1-0.1)µ⁻²=0.0729
2
p(x=0)= 10*0.01*0.729= 0.0729

11. DISTRIBUCIÓN POISSON
Sea X ͠ poisson (4). Determine
a) P(X=1)
b) P(X=0)
c) P(X<2)
d) P(X>1)

12. Si se nos dice que poisson(4) sustituiremos los
valores en la siguiente ecuación.
p(x)=P(X=x)= e⁻ʵ λˣ
x!
λ=4
X=1
a) P(X=1)
p(x)=P(X=1)= e⁻ ´4¹ =0.0733
1!

13. b) P(X=0)
λ=4
X=0
p(x)=P(X=1)= e⁻ ´4⁰ =0.0183
0!