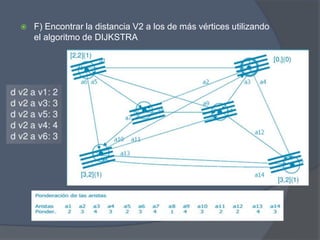
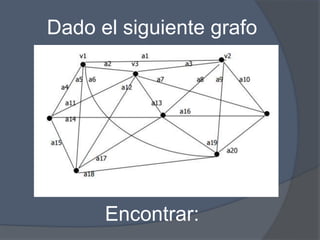
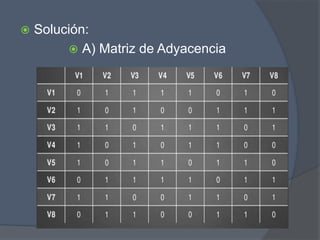
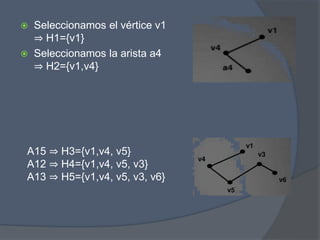
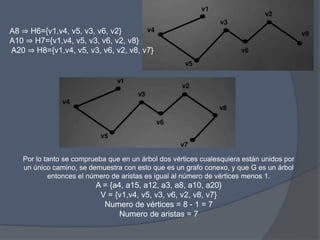
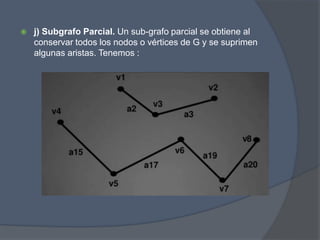
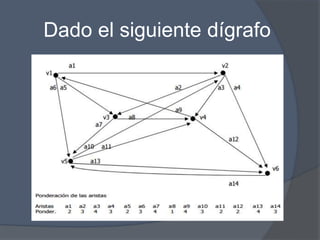
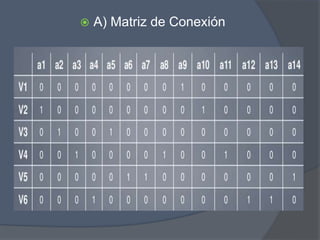
El documento presenta un problema de grafos que involucra encontrar la matriz de adyacencia y de incidencia de un grafo, determinar si es conexo, simple, regular o completo, y encontrar cadenas, ciclos, árbol generador y demostrar si es euleriano o hamiltoniano. También presenta un problema de dígrafos que involucra encontrar la matriz de conexión, cadenas, ciclos, y demostrar si es fuertemente conexo, además de encontrar distancias utilizando el algoritmo de Dijkstra.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
VICERRECTORADO ACADÉMICO
UNIVERSIDAD FERMÍN TORO
FACULTAD INGENIERÍA
Richard Nieto
V-21.142.293

2. Dado el siguiente grafo
Encontrar:

3.  a) Matriz de
adyacencia
 b) Matriz de incidencia
 c) Es conexo?
Justifique su
respuesta
 d) Es simple?.
Justifique su
respuesta
 e) Es regular?.
Justifique su
respuesta
 f) Es completo?
g) Una cadena simple no
elemental de grado 6
h) Un ciclo no simple de
grado 5
i) Árbol generador
aplicando el algoritmo
constructor
j) Subgrafo parcial
k) Demostrar si es
euleriano aplicando el
algoritmo de Fleury
l) Demostrar si es
hamiltoniano

4.  Solución:
 A) Matriz de Adyacencia

5.  B) Matriz de incidencia:

6.  c) Es conexo?
Se dice Conexo si para cualquier par de vértices de a y b
en G existe al menos una trayectoria (una secuencia
de vértices adyacentes que no repita vértices) de a á
b. De acuerdo con la definición, si es conexo ya que,
para todo par de vértices se encuentran conectados o
tienen un camino que los una.
d) Es simple?
Si es un grafo simple, debido a que se cumple que
ningún vértice tiene lazo, además cada vértice esta
unido por una sola arista.
e) Es Regular?. No es un grafo regular, ya que hay
vértices que tienen grados o valencias diferentes.
f) Es Completo?. podemos decir que no es nompleto,
porque posee aristas paralelas y más de una arista por
cada par de vértices, dando origen a los sub-grafos.

7.  G) Una cadena simple no elemental de
grado 6.
Una cadena simple es una secuencia finita
alternada de vértices y aristas, sin repetir
aristas, no elemental indica que puede
repetirse los vértices. El grado nos indica la
cantidad de aristas que debe contener la
cadena, en esta oportunidad son seis como
por ejemplo: V3= GRADO 6
V6= GRADO 6
h) Un ciclo no simple de grado 5.
Como sabemos, Es un ciclo que no es una
cadena simple. No se puede demostrar, ya
que todas las aristas son distintas del grafo.
No hay cadenas no simples de ningún grado.

8. I) Árbol generador aplicando el algoritmo
constructor.
 Paso 1: Seleccionar un vértice S1, hacer
H1={S1}
 Paso 2: Seleccionamos una arista a1 que
tenga un extremo en H1 y el otro extremo
en un vértice S2 ∉ H1. Hacer H1 ∪ {S2}
 Paso 3: Seleccionamos una arista a2 que
tenga un extremo en H2, y el otro extremo
en un vértice S3 ∉ H2. Hacer H2 ∪ {S3}

9.  Seleccionamos el vértice v1
⇒ H1={v1}
 Seleccionamos la arista a4
⇒ H2={v1,v4}
A15 ⇒ H3={v1,v4, v5}
A12 ⇒ H4={v1,v4, v5, v3}
A13 ⇒ H5={v1,v4, v5, v3, v6}

10. A8 ⇒ H6={v1,v4, v5, v3, v6, v2}
A10 ⇒ H7={v1,v4, v5, v3, v6, v2, v8}
A20 ⇒ H8={v1,v4, v5, v3, v6, v2, v8, v7}
Por lo tanto se comprueba que en un árbol dos vértices cualesquiera están unidos por
un único camino, se demuestra con esto que es un grafo conexo, y que G es un árbol
entonces el número de aristas es igual al número de vértices menos 1.
A = {a4, a15, a12, a3, a8, a10, a20}
V = {v1,v4, v5, v3, v6, v2, v8, v7}
Numero de vértices = 8 - 1 = 7
Numero de aristas = 7

11.  j) Subgrafo Parcial. Un sub-grafo parcial se obtiene al
conservar todos los nodos o vértices de G y se suprimen
algunas aristas. Tenemos :

12.  K) Demostrar si es euleriano aplicando el
algoritmo de Fleury.
R: para que el grafo sea euleriano a partir de un vértice
cualquiera de G se puede construir una cadena simple de
manera que no se repitan las aristas y no se adopten aristas
de corte a no ser que no se encuentre otra alternativa, al
haber acabado las aristas decimos que tenemos un tour
euleriano. Luego de experimentar el grafo sin repetir aristas,
no ha sido posible encontrar un camino euleriano donde no
se repitan aristas, por lo tanto no se cumple que el Grafo
sea Euleriano

13. K) Demostrar si es Hamiltoniano

14. Dado el siguiente dígrafo

15.  a) Encontrar matriz de conexión
 b) Es simple?. Justifique su respuesta
 c) Encontrar una cadena no simple no
elemental de grado 5
 d) Encontrar un ciclo simple e) Demostrar
si es fuertemente conexo utilizando la
matriz de accesibilidad
 f) Encontrar la distancia de v2 a los demás
vértices utilizando el algoritmo de Dijkstra

16.  A) Matriz de Conexión

17. B) Es simple?.
R: Se cumple que el Dígrafo es simple, ya que no tiene lazos y no
existen arcos paralelos que partan de un mismo vértice a otro.
C) Encontrar una cadena no simple no elemental de grado 5
R: En las cadenas no simples se pueden repetir los arcos durante
el recorrido y que sea no elemental, también nos permite repetir
vértices. El grado 5 nos indica el número de arcos que tendrá
nuestra cadena.
T = [v4, α9, v1, α5, v3, α8, v4, α9, v1, α6, v5]
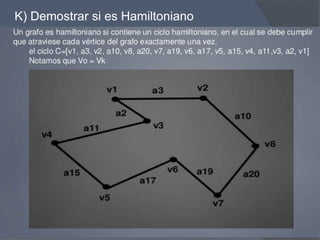
D) Encontrar un ciclo simple
R: El ciclo simple inicia y termina con el mismo vértice y en ella no
se pueden repetir arcos.
C = [v6, α14, v5, α11, v4, α9, v1, α1, v2, α4, v6 ]

18.  e) Demostrar si es fuertemente conexo utilizando la matriz de
accesibilidad
R: Para comprobar que un grafo es conexo podemos realizar los siguientes
pasos:
1) Hallar la matriz de adyacencia y se eleva a la enésima potencia.
2) Se calcula la suma de las potencias de A hasta An.
3) Si todos sus elementos son distintos de cero, el grafo es conexo
Matriz de Adyacencia

19. Elevamos la matriz al cuadrado
y así hallamos los caminos de tamaño 2
Elevamos la matriz al cubo
y así hallamos los caminos
de tamaño 3
Hacemos lo mismo para encontrar los caminos de tamaño 4 y 5, respectivamente

20. Para calcular la matriz de accesibilidad, utilizamos la siguiente fórmula:
Acc(D) = bin [I6 + M + M^2 + M^3 + M^4 + M^5 ]
Acc(D) = bin
Luego transformamos la matriz de
la manera siguiente:
a) Componente que sea igual a
cero, permanece como cero.
b) b) Componente diferente de
cero, convertirla a 1.
Acc(D) = bin
Como la matriz Acc(D) no tiene componentes
nulas se dice entonces que el dígrafo es
fuertemente conexo.

21.  F) Encontrar la distancia V2 a los de más vértices utilizando
el algoritmo de DIJKSTRA