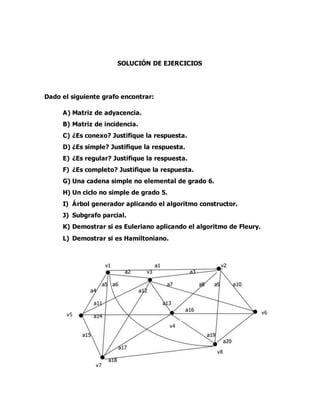
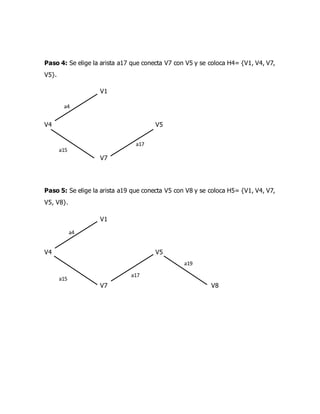
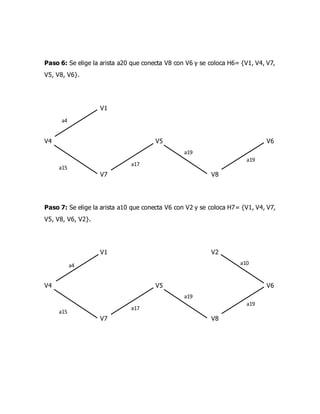
El documento presenta la resolución de varios ejercicios sobre grafos y dígrafos. Se pide encontrar la matriz de adyacencia, matriz de incidencia, determinar si es conexo, simple, regular o completo para un grafo dado. También se pide construir un árbol generador, subgrafo parcial, y determinar si es Euleriano o Hamiltoniano. Para un dígrafo dado, se pide encontrar la matriz de conexión, cadena no simple, ciclo simple y determinar si es fuertemente conexo usando la matriz de accesibilidad. Finalmente,

1. UNIVERSIDAD“FERMÍN TORO”
VICERECTORADO ACADÉMICO
FACULTAD DE INGENIERÍA
ESCUELA DE INGENIERÍA EN COMPUTACIÓN
EJERCICIO RESUELTO
GRAFOS & DIGRAFOS.
ALUMNO:
VICTOR ESCALONA
C.I: 25254238

2. SOLUCIÓN DE EJERCICIOS
Dado el siguiente grafo encontrar:
A) Matriz de adyacencia.
B) Matriz de incidencia.
C) ¿Es conexo? Justifique la respuesta.
D) ¿Es simple? Justifique la respuesta.
E) ¿Es regular? Justifique la respuesta.
F) ¿Es completo? Justifique la respuesta.
G) Una cadena simple no elemental de grado 6.
H) Un ciclo no simple de grado 5.
I) Árbol generador aplicando el algoritmo constructor.
J) Subgrafo parcial.
K) Demostrar si es Euleriano aplicando el algoritmo de Fleury.
L) Demostrar si es Hamiltoniano.
v5 v6
v8
v7
v4

3. 1.A) La matriz de adyacencia es una matriz cuadrada A, en la que sus entradas
AIJ pertenecen al número de aristas que van desde VI hasta su vértice VJ.
0 1 1 1 0 0 1 1
1 0 1 0 1 1 0 1
1 1 0 1 1 1 1 0
1 0 1 0 1 0 1 0
0 1 1 1 0 1 1 1
0 1 1 0 1 0 0 1
1 0 1 1 1 0 0 1
1 1 0 0 1 1 1 0
1.B) La matriz de incidencia es una matriz M, en la que sus entradas MIJ son el
número de veces que la arista J coincide en el vértice I.
1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0
0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
0 0 0 0 1 0 0 0 0 0 0 1 0 0 7 0 1 1 0 0
0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
A=
M=

4. 1.C) El grafo dado es conexo debido a que existe una cadena entre cualquier par
de vértices.
1.D) El grafo es simple ya que no tiene ciclos y no posee mas de una arista
uniendo un par de vértices, se puede observar que para cada par de vértices que
están unidos dicha unión es a través de una sola arista.
1.E) El grafo estudiado no es regular debido a que el grado de incidencia del
vértice V1=5 y el del vértice V3, por lo tanto para que un grafo sea regular todos
los vértices deberían de tener el mismo grado de incidencia.
1.F) Se puede observar que el grafo es completo porque el vértice V1 no esta
conectado al vértice V5 y para que sea completo cada vértice debe estar
conectado a cualquier otro vértice distinto.
1.G) Una simple no elemental de grado 6 (se repite el vértice V4) es: V6 a20 V8
a19 V4 a17 V7 a15 V5 A11 V3 a13 V4.
1.H) Un ciclo no simple de grado 5 (se repite la arista a11) es: V3 a11 V5 a15 V7
a17 V4 a13 V3 a11 V5.
1.I) Árbol generador aplicando el algoritmo constructor:
Paso 1: Elegir S1=V1, y se coloca H1= {V1}

5. a4
a4
a15
Paso 2: Se elige a a4 que conecta a V1 con V4 y se coloca H2= {V1,V4}
V1
V4
Paso 3: Se elige la arista a15 que conecta V4 con V7 y se coloca H3= {V1, V4,
V7}.
V1
V4
V7

6. a4
a15
a17
a4
a15
a17
a19
Paso 4: Se elige la arista a17 que conecta V7 con V5 y se coloca H4= {V1, V4, V7,
V5}.
V1
V4 V5
V7
Paso 5: Se elige la arista a19 que conecta V5 con V8 y se coloca H5= {V1, V4, V7,
V5, V8}.
V1
V4 V5
V7 V8

7. a15
a17
a19
a4
a19
a15
a17
a19
a19
a4 a10
Paso 6: Se elige la arista a20 que conecta V8 con V6 y se coloca H6= {V1, V4, V7,
V5, V8, V6}.
V1
V4 V5 V6
V7 V8
Paso 7: Se elige la arista a10 que conecta V6 con V2 y se coloca H7= {V1, V4, V7,
V5, V8, V6, V2}.
V1 V2
V4 V5 V6
V7 V8

8. a15
a17
a19
a20
a4 a10
a3
a4
a11
a3
a1
a2
Paso 8: Se elige la arista a3 que conecta V2 con V3 y se coloca H7= {V1, V4, V7,
V5, V8, V6, V2, V3}. Obteniendo de esta manera el siguiente árbol generador.
V1 V3 V2
V4 V5 V6
V7 V8
1.J) Con V= {V1, V4, V3, V2} y A= {a4, a2, a11, a3, a1}
V1
V4 V2
V3

9. a15
a17
a19
a20
a4 a10
a3a2
1.K) El grafo no es euleriano debido a que no es posible la construcción de un
ciclo euleriano, ya que no todos los vértices tienen grado par.
1.L) El numero de vértices que posee el grafo es8, el grado de V1 es Gr(V1) ≥ 4,
el de V2 es Gr(V2) ≥ 4, el de V8 es Gr(V8) ≥ 4, además de ser un grafo simple,
por lo tanto de es grafo es Hamiltoniano. En la siguiente figura podremos ver un
ciclo Hamiltoniano.
V1 V3 V2
V4 V5 V6
V7 V8
Dado el siguiente dígrafo encontrar:
A) Matriz de conexión.
B) ¿Es simple? Justifique la respuesta.
C) Una cadena no simple no elemental de grado 5.
D) Un ciclo simple.
E) Demostrar si es fuertemente conexo utilizando la matriz de
accesibilidad.

10. F) La distancia de V2 a los demás vértices utilizando el algoritmo
de dijkstra.

11. 2.A) Matriz de Conexión
2.B) Se puede decir que el dígrafo es simple ya que no posee ni arcos ni lazos
paralelos.
2.C) Una cadena no simple elemental de grado 5 (se repite el vértice V4) es: V4
a3 V2 a2 V3 a7 V5 a11 V4 a12 V6.
2.D) Un ciclo simple es: V1 a6 V5 a11 V4 a9 V1
2.E) Utilizando la matriz de accesibilidad demostrar si es fuertemente conexo.
0 1 1 0 1 0
0 0 1 1 0 1
0 0 0 1 1 0
1 0 0 0 0 1
0 1 0 0 0 1
0 0 0 0 1 0
0 1 1 0 1 0
0 0 1 1 0 1
0 0 0 1 1 0
1 0 0 0 0 1
0 1 0 0 0 1
0 0 0 0 1 0
MC=
MC=

12. 0 1 1 1 1 1
1 0 0 1 1 0
1 1 1 1 0 1
0 1 1 0 1 0
1 0 1 1 0 1
0 1 0 1 0 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
0 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
MC2=
MC3=
MC4=

13. 2.F) Sea la distancia DI la distancia mas corta del vértice VI al vértice V2.
Paso1: D0 (V2) = 0; U0= V2
Paso2: D1 (V1) = min (Inf, Inf) = Inf
D1 (V3) = min (Inf, 3) = 3
D1 (V4) = min (Inf, 4) = 4
D1 (V5) = min (Inf, Inf) = Inf
D1 (V6) = min (Inf, 3) = 3
U1= V3; D1 (U1) = 3
Paso 3: D2 (V1) = min (Inf, 3 + Inf) = Inf
D2 (V4) = min (4, 3 + 1) = 4
D2 (V5) = min (Inf, 3 + 4) = 7
D2 (V6) = min (Inf, 3) =3
U2= V6; D2 (U2) = 3
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
MC5=

14. Paso 4: D3 (V1) = min (Inf, 3 + Inf) =Inf
D3 (V4) = min (4, 3 + Inf) =Inf
D3 (V5) = min (7, 3 + 3) =6
U3= V4; D3 (U3) = 4
Paso 5: D4 (V1) = min (Inf, 4 + 4) =8
D4 (V5) = min (6, 4 + Inf) =6
U4= V5; D4 (U4) = 6
Paso 6: D5 (V1) = min (8, 6 + Inf) =8
U5= V1; D5 (V1) = 8
Entonces D(V2, V1)= 8, D(V2, V2)= 0, D(V2, V3)= 3, D(V2, V4)= 4, D(V2,V5)= 6
y D(V2,V6)=3.